ปัจจัยกำหนดเมทริกซ์และคุณสมบัติของเมทริกซ์ คุณสมบัติบางประการของดีเทอร์มิแนนต์ วิธีการคำนวณดีเทอร์มิแนนต์ที่มีประสิทธิภาพ
เมทริกซ์จตุรัส กคำสั่ง nคุณสามารถเปรียบเทียบตัวเลข det ก(หรือ | ก| หรือ ) เรียกเธอ ปัจจัยกำหนด ด้วยวิธีต่อไปนี้:
ดีเทอร์มิแนนต์เมทริกซ์ กเรียกเธอด้วย ปัจจัยกำหนด . กฎสำหรับการคำนวณดีเทอร์มิแนนต์สำหรับเมทริกซ์ลำดับ เอ็นค่อนข้างยากที่จะเข้าใจและนำไปใช้ได้ อย่างไรก็ตาม ทราบวิธีการต่างๆ ที่ทำให้สามารถใช้การคำนวณปัจจัยกำหนดลำดับที่สูงโดยพิจารณาจากปัจจัยกำหนดลำดับที่ต่ำกว่าได้ วิธีหนึ่งขึ้นอยู่กับคุณสมบัติของการขยายตัวของดีเทอร์มิแนนต์ไปเป็นองค์ประกอบของอนุกรมหนึ่งๆ (คุณสมบัติ 7) ในเวลาเดียวกัน เราทราบว่าขอแนะนำให้สามารถคำนวณปัจจัยกำหนดลำดับต่ำ (1, 2, 3) ตามคำจำกัดความได้
การคำนวณปัจจัยกำหนดลำดับที่ 2 แสดงไว้ในแผนภาพ:
ตัวอย่างที่ 4.1ค้นหาปัจจัยกำหนดของเมทริกซ์
เมื่อคำนวณดีเทอร์มิแนนต์ลำดับที่ 3 จะสะดวกในการใช้งาน กฎสามเหลี่ยม (หรือซาร์รัส) ซึ่งสามารถเขียนเป็นสัญลักษณ์ได้ดังนี้
ตัวอย่างที่ 4.2คำนวณดีเทอร์มิแนนต์ของเมทริกซ์
เดช ก = 5*1*(-3) + (-2)*(-4)*6 + 3*0*1 — 6*1*1 — 3*(-2)*(-3) — 0*(-4)*5 = -15+48-6-18 = 48-39 = 9.
ให้เรากำหนดคุณสมบัติพื้นฐานของดีเทอร์มิแนนต์ที่มีอยู่ในดีเทอร์มิแนนต์ของลำดับทั้งหมด เราจะอธิบายคุณสมบัติเหล่านี้บางส่วนโดยใช้ปัจจัยกำหนดลำดับที่สาม
คุณสมบัติ 1 (“ความเท่าเทียมกันของแถวและคอลัมน์”) ดีเทอร์มิแนนต์จะไม่เปลี่ยนแปลงหากแถวถูกแทนที่ด้วยคอลัมน์ และในทางกลับกัน กล่าวอีกนัยหนึ่ง
ต่อไปนี้ เราจะเรียกแถวและคอลัมน์เพียงอย่างเดียว แถวของดีเทอร์มิแนนต์ .
คุณสมบัติ 2 . เมื่ออนุกรมคู่ขนานสองชุดถูกจัดเรียงใหม่ ดีเทอร์มิแนนต์จะเปลี่ยนเครื่องหมาย
คุณสมบัติ 3 . ดีเทอร์มิแนนต์ที่มีอนุกรมเหมือนกัน 2 ชุดจะมีค่าเท่ากับศูนย์
คุณสมบัติ 4 . ตัวประกอบร่วมขององค์ประกอบของอนุกรมของดีเทอร์มิแนนต์ใดๆ สามารถนำออกจากเครื่องหมายของดีเทอร์มิแนนต์ได้
จากคุณสมบัติที่ 3 และ 4 ดังนี้ ว่าถ้าองค์ประกอบทั้งหมดของอนุกรมหนึ่งเป็นสัดส่วนกับองค์ประกอบที่สอดคล้องกันของอนุกรมคู่ขนาน แล้วดีเทอร์มิแนนต์นั้นจะเท่ากับศูนย์
จริงหรือ,
คุณสมบัติ 5 . หากองค์ประกอบของอนุกรมใดๆ ของดีเทอร์มิแนนต์เป็นผลรวมของสองเทอม ดีเทอร์มิแนนต์ก็สามารถแยกย่อยเป็นผลรวมของดีเทอร์มิแนนต์ที่ตรงกันสองตัวได้
ตัวอย่างเช่น,
คุณสมบัติ 6. (“การเปลี่ยนแปลงเบื้องต้นของดีเทอร์มิแนนต์”) ดีเทอร์มิแนนต์จะไม่เปลี่ยนแปลงหากมีการเพิ่มองค์ประกอบที่สอดคล้องกันของอนุกรมคู่ขนานเข้ากับองค์ประกอบของอนุกรมหนึ่ง คูณด้วยตัวเลขใดๆ
ตัวอย่างที่ 4.3. พิสูจน์ว่า
วิธีแก้ปัญหา: เราจะเรียนรู้โดยใช้คุณสมบัติ 5, 4 และ 3
คุณสมบัติเพิ่มเติมของดีเทอร์มิแนนต์เกี่ยวข้องกับแนวคิดของการเสริมรองและพีชคณิต
ส่วนน้อยองค์ประกอบบางอย่าง อ๋อปัจจัยกำหนด ไม่มีไทย ลำดับเรียกว่าปัจจัยกำหนด n- ลำดับที่ 1 ได้มาจากต้นฉบับโดยขีดฆ่าแถวและคอลัมน์ตรงจุดตัดขององค์ประกอบที่เลือก กำหนด มิจ
ส่วนเสริมพีชคณิตองค์ประกอบ ไอจของดีเทอร์มิแนนต์เรียกว่าไมเนอร์ ซึ่งมีเครื่องหมายบวก ถ้าเป็นผลรวม ฉัน+เจเป็นเลขคู่และมีเครื่องหมายลบหากจำนวนนี้เป็นเลขคี่ กำหนด ไอจ:
คุณสมบัติ 7 (“การสลายตัวของดีเทอร์มิแนนต์เป็นองค์ประกอบของอนุกรมหนึ่งๆ”) ดีเทอร์มิแนนต์เท่ากับผลรวมของผลิตภัณฑ์ขององค์ประกอบของอนุกรมหนึ่งๆ และการเสริมพีชคณิตที่เกี่ยวข้อง
ต่อไปนี้เราจะสรุปคุณสมบัติต่างๆ ที่มักใช้ในการคำนวณดีเทอร์มิแนนต์ในหลักสูตรมาตรฐานของคณิตศาสตร์ชั้นสูง นี่เป็นหัวข้อเสริมที่เราจะอ้างอิงจากส่วนอื่นๆ ตามความจำเป็น
ดังนั้น ให้เมทริกซ์จตุรัสบางตัว $A_(n\times n)=\left(\begin(array) (cccc) a_(11) & a_(12) & \ldots & a_(1n) \\ a_(21) ได้รับ & a_(22) & \ldots & a_(2n) \\ \ldots & \ldots & \ldots & \ldots \\ a_(n1) & a_(n2) & \ldots & a_(nn) \\ \ สิ้นสุด (อาร์เรย์) \right)$ เมทริกซ์จตุรัสทุกเมทริกซ์มีคุณสมบัติที่เรียกว่าดีเทอร์มิแนนต์ (หรือดีเทอร์มิแนนต์) ฉันจะไม่ลงลึกถึงแก่นแท้ของแนวคิดนี้ที่นี่ หากต้องการคำชี้แจง โปรดเขียนเกี่ยวกับเรื่องนี้ในฟอรัม และเราจะพูดถึงปัญหานี้โดยละเอียดยิ่งขึ้น
ดีเทอร์มีแนนต์ของเมทริกซ์ $A$ แสดงเป็น $\Delta A$, $|A|$ หรือ $\det A$ คำสั่งเด็ดขาดเท่ากับจำนวนแถว (คอลัมน์) ในนั้น
- ค่าของดีเทอร์มิแนนต์จะไม่เปลี่ยนแปลงหากแถวถูกแทนที่ด้วยคอลัมน์ที่เกี่ยวข้อง เช่น $\เดลต้า A=\เดลต้า A^T$
แสดงซ่อน
มาแทนที่แถวในนั้นด้วยคอลัมน์ตามหลักการ: "มีแถวแรก - มีคอลัมน์แรก", "มีแถวที่สอง - มีคอลัมน์ที่สอง":
ลองคำนวณดีเทอร์มิแนนต์ผลลัพธ์: $\left| \begin(array) (cc) 2 & 9 \\ 5 & 4 \end(array) \right|=2\cdot 4-9\cdot 5=-37$. อย่างที่คุณเห็น ค่าของดีเทอร์มิแนนต์ไม่มีการเปลี่ยนแปลงเนื่องจากการแทนที่
- หากคุณสลับสองแถว (คอลัมน์) ของดีเทอร์มิแนนต์ เครื่องหมายของดีเทอร์มิแนนต์จะเปลี่ยนไปในทางตรงกันข้าม
ตัวอย่างการใช้คุณสมบัตินี้: show\hide
พิจารณาดีเทอร์มิแนนต์ $\left| \begin(array) (cc) 2 & 5 \\ 9 & 4 \end(array) \right|$. มาหาค่าของมันโดยใช้สูตรหมายเลข 1 จากหัวข้อการคำนวณปัจจัยกำหนดของลำดับที่สองและสาม:
$$\ซ้าย| \begin(array) (cc) 2 & 5 \\ 9 & 4 \end(array) \right|=2\cdot 4-5\cdot 9=-37.$$
ตอนนี้ขอสลับบรรทัดแรกและบรรทัดที่สอง เราได้ดีเทอร์มิแนนต์ $\left| \begin(array) (cc) 9 & 4 \\ 2 & 5 \end(array) \right|$. ลองคำนวณดีเทอร์มิแนนต์ผลลัพธ์: $\left| \begin(array) (cc) 9 & 4 \\ 2 & 5 \end(array) \right|=9\cdot 5-4\cdot 2=37$. ดังนั้น ค่าของดีเทอร์มิแนนต์เดิมคือ (-37) และค่าของดีเทอร์มิแนนต์ที่มีลำดับแถวที่เปลี่ยนแปลงคือ $-(-37)=37$ เครื่องหมายของดีเทอร์มิแนนต์เปลี่ยนไปในทิศทางตรงกันข้าม
- ดีเทอร์มิแนนต์ที่องค์ประกอบทั้งหมดของแถว (คอลัมน์) เท่ากับศูนย์จะเท่ากับศูนย์
ตัวอย่างการใช้คุณสมบัตินี้: show\hide
เนื่องจากอยู่ในดีเทอร์มิแนนต์ $\left| \begin(array) (ccc) -7 & 10 & 0\\ -9 & 21 & 0\\ 2 & -3 & 0 \end(array) \right|$ องค์ประกอบทั้งหมดของคอลัมน์ที่สามเป็นศูนย์ จากนั้น ดีเทอร์มิแนนต์เป็นศูนย์ เช่น $\ซ้าย| \begin(array) (ccc) -7 & 10 & 0\\ -9 & 21 & 0\\ 2 & -3 & 0 \end(array) \right|=0$.
- ดีเทอร์มิแนนต์ที่องค์ประกอบทั้งหมดของแถวใดแถวหนึ่ง (คอลัมน์) เท่ากับองค์ประกอบที่สอดคล้องกันของอีกแถวหนึ่ง (คอลัมน์) จะเท่ากับศูนย์
ตัวอย่างการใช้คุณสมบัตินี้: show\hide
เนื่องจากอยู่ในดีเทอร์มิแนนต์ $\left| \begin(array) (ccc) -7 & 10 & 0\\ -7 & 10 & 0\\ 2 & -3 & 18 \end(array) \right|$ องค์ประกอบทั้งหมดของแถวแรกเท่ากับค่าที่สอดคล้องกัน องค์ประกอบของแถวที่สอง จากนั้นดีเทอร์มิแนนต์จะเท่ากับศูนย์ เช่น $\ซ้าย| \begin(array) (ccc) -7 & 10 & 0\\ -7 & 10 & 0\\ 2 & -3 & 18 \end(array) \right|=0$.
- หากในตัวกำหนดองค์ประกอบทั้งหมดของแถวหนึ่ง (คอลัมน์) เป็นสัดส่วนกับองค์ประกอบที่สอดคล้องกันของอีกแถวหนึ่ง (คอลัมน์) ดังนั้นปัจจัยดังกล่าวจะเท่ากับศูนย์
ตัวอย่างการใช้คุณสมบัตินี้: show\hide
เนื่องจากอยู่ในดีเทอร์มิแนนต์ $\left| \begin(array) (ccc) -7 & 10 & 28\\ 5 & -3 & 0\\ -15 & 9 & 0 \end(array) \right|$ แถวที่สองและสามเป็นสัดส่วน กล่าวคือ $r_3=-3\cdot(r_2)$ ดังนั้นดีเทอร์มิแนนต์จะเท่ากับศูนย์ นั่นคือ $\ซ้าย| \begin(array) (ccc) -7 & 10 & 28\\ 5 & -3 & 0\\ -15 & 9 & 0 \end(array) \right|=0$.
- หากองค์ประกอบทั้งหมดของแถว (คอลัมน์) มีตัวประกอบร่วมกัน ก็สามารถนำปัจจัยนี้ออกจากเครื่องหมายดีเทอร์มิแนนต์ได้
ตัวอย่างการใช้คุณสมบัตินี้: show\hide
พิจารณาดีเทอร์มิแนนต์ $\left| \begin(array) (cc) -7 & 10 \\ -9 & 21 \end(array) \right|$. โปรดสังเกตว่าองค์ประกอบทั้งหมดในแถวที่สองหารด้วย 3 ลงตัว:
$$\ซ้าย| \begin(array) (cc) -7 & 10 \\ -9 & 21 \end(array) \right|=\left| \begin(array) (cc) -7 & 10 \\ 3\cdot(-3) & 3\cdot 7 \end(array) \right|$$
หมายเลข 3 เป็นตัวประกอบร่วมขององค์ประกอบทั้งหมดในแถวที่สอง ลองเอาเครื่องหมายสามตัวออกจากเครื่องหมายดีเทอร์มิแนนต์:
$$\ซ้าย| \begin(array) (cc) -7 & 10 \\ -9 & 21 \end(array) \right|=\left| \begin(array) (cc) -7 & 10 \\ 3\cdot(-3) & 3\cdot 7 \end(array) \right|= 3\cdot \left| \begin(array) (cc) -7 & 10 \\ -3 & 7 \end(array) \right| $$
- ดีเทอร์มิแนนต์จะไม่เปลี่ยนแปลงหากองค์ประกอบทั้งหมดของแถวใดแถวหนึ่ง (คอลัมน์) เราเพิ่มองค์ประกอบที่สอดคล้องกันของอีกแถวหนึ่ง (คอลัมน์) คูณด้วยตัวเลขใดก็ได้
ตัวอย่างการใช้คุณสมบัตินี้: show\hide
พิจารณาดีเทอร์มิแนนต์ $\left| \begin(array) (ccc) -7 & 10 & 0\\ -9 & 21 & 4 \\ 2 & -3 & 1 \end(array) \right|$. ลองเพิ่มองค์ประกอบที่สอดคล้องกันของบรรทัดที่สามเข้ากับองค์ประกอบของบรรทัดที่สอง คูณด้วย 5 การกระทำนี้เขียนได้ดังนี้: $r_2+5\cdot(r_3)$ บรรทัดที่สองจะมีการเปลี่ยนแปลง บรรทัดที่เหลือจะไม่เปลี่ยนแปลง
$$\ซ้าย| \begin(array) (ccc) -7 & 10 & 0\\ -9 & 21 & 4 \\ 2 & -3 & 1 \end(array) \right| \begin(array) (l) \phantom(0)\\ r_2+5\cdot(r_3)\\ \phantom(0) \end(array)= \left| \begin(array) (ccc) -7 & 10 & 0\\ -9+5\cdot 2 & 21+5\cdot (-3) & 4+5\cdot 1 \\ 2 & -3 & 1 \end (อาร์เรย์) \right|= \left| \begin(array) (ccc) -7 & 10 & 0\\ 1 & 6 & 9 \\ 2 & -3 & 1 \end(array) \right| $$
- หากแถวใดแถวหนึ่ง (คอลัมน์) ในดีเทอร์มิแนนต์เป็นผลรวมเชิงเส้นของแถวอื่น (คอลัมน์) ดีเทอร์มิแนนต์จะเท่ากับศูนย์
ตัวอย่างการใช้คุณสมบัตินี้: show\hide
ให้ฉันอธิบายทันทีว่าวลี "การรวมกันเชิงเส้น" หมายถึงอะไร ให้เรามีแถว (หรือคอลัมน์): $A_1$, $A_2$,..., $A_s$. การแสดงออก
$$ k_1\cdot A_1+k_2\cdot A_2+\ldots+k_s\cdot A_s, $$
โดยที่ $k_i\in R$ เรียกว่าผลรวมเชิงเส้นของแถว (คอลัมน์) $A_1$, $A_2$,..., $A_s$
ตัวอย่างเช่น พิจารณาปัจจัยกำหนดต่อไปนี้:
$$\ซ้าย| \begin(array) (cccc) -1 & 2 & 3 & 0\\ -2 & -4 & -5 & 1\\ 5 & 0 & 7 & 10 \\ -13 & -8 & -16 & -7 \end(อาร์เรย์) \right| $$
ในดีเทอร์มิแนนต์นี้ แถวที่สี่สามารถแสดงเป็นผลรวมเชิงเส้นของสามแถวแรกได้:
$$ r_4=2\cdot(r_1)+3\cdot(r_2)-r_3 $$
ดังนั้นดีเทอร์มิแนนต์ที่เป็นปัญหาจึงเท่ากับศูนย์
- ถ้าแต่ละองค์ประกอบของแถวที่ k บางแถว (คอลัมน์ที่ k) ของดีเทอร์มิแนนต์เท่ากับผลรวมของสองเทอม ดังนั้นดีเทอร์มิแนนต์นั้นจะเท่ากับผลรวมของดีเทอร์มิแนนต์ โดยอันแรกมีเทอมแรกใน แถวที่ k (คอลัมน์ที่ k) และปัจจัยที่สองของแถวที่ k (คอลัมน์ที่ k) มีเทอมที่สอง องค์ประกอบอื่นๆ ของปัจจัยกำหนดเหล่านี้เหมือนกัน
ตัวอย่างการใช้คุณสมบัตินี้: show\hide
พิจารณาดีเทอร์มิแนนต์ $\left| \begin(array) (ccc) -7 & 10 & 0\\ -9 & 21 & 4 \\ 2 & -3 & 1 \end(array) \right|$. เรามาเขียนองค์ประกอบของคอลัมน์ที่สองดังนี้: $\left| \begin(array) (ccc) -7 & 3+7 & 0\\ -9 & 21+0 & 4 \\ 2 & 5+(-8) & 1 \end(array) \right|$. จากนั้นดีเทอร์มิแนนต์ดังกล่าวจะเท่ากับผลรวมของดีเทอร์มิแนนต์สองตัว:
$$\ซ้าย| \begin(array) (ccc) -7 & 10 & 0\\ -9 & 21 & 4 \\ 2 & -3 & 1 \end(array) \right|= \left| \begin(array) (ccc) -7 & 3+7 & 0\\ -9 & 21+0 & 4 \\ 2 & 5+(-8) & 1 \end(array) \right|= \left| \begin(array) (ccc) -7 & 3 & 0\\ -9 & 21 & 4 \\ 2 & 5 & 1 \end(array) \right|+ \left| \begin(array) (ccc) -7 & 7 & 0\\ -9 & 0 & 4 \\ 2 & -8 & 1 \end(array) \right| $$
- ดีเทอร์มิแนนต์ของผลคูณของเมทริกซ์จตุรัสสองตัวที่มีลำดับเดียวกันจะเท่ากับผลคูณของดีเทอร์มิแนนต์ของเมทริกซ์เหล่านี้ กล่าวคือ $\det(A\cdot B)=\det A\cdot \det B$. จากกฎนี้ เราจะได้สูตรต่อไปนี้: $\det \left(A^n \right)=\left(\det A \right)^n$
- ถ้าเมทริกซ์ $A$ ไม่ใช่เอกพจน์ (นั่นคือ ดีเทอร์มิแนนต์ของมันไม่เท่ากับศูนย์) ดังนั้น $\det \left(A^(-1)\right)=\frac(1)(\det A)$
สูตรคำนวณดีเทอร์มิแนนต์
สำหรับปัจจัยกำหนดลำดับที่สองและสาม สูตรต่อไปนี้ถูกต้อง:
\begin(สมการ) \Delta A=\left| \begin(array) (cc) a_(11) & a_(12) \\ a_(21) & a_(22) \end(array) \right|=a_(11)\cdot a_(22)-a_( 12)\cdot a_(21) \end(สมการ) \begin(สมการ) \begin(ชิด) & \Delta A=\left| \begin(array) (ccc) a_(11) & a_(12) & a_(13) \\ a_(21) & a_(22) & a_(23) \\ a_(31) & a_(32) & a_(33) \end(array) \right|= a_(11)\cdot a_(22)\cdot a_(33)+a_(12)\cdot a_(23)\cdot a_(31)+a_(21) )\cdot a_(32)\cdot a_(13)-\\ & -a_(13)\cdot a_(22)\cdot a_(31)-a_(12)\cdot a_(21)\cdot a_(33) )-a_(23)\cdot a_(32)\cdot a_(11)\end(ชิด)\end(สมการ)
ตัวอย่างการใช้สูตร (1) และ (2) อยู่ในหัวข้อ "สูตรคำนวณดีเทอร์มิแนนต์ของลำดับที่สองและสาม ตัวอย่างการคำนวณดีเทอร์มิแนนต์"
ดีเทอร์มีแนนต์ของเมทริกซ์ $A_(n\times n)$ สามารถขยายได้ในแถวที่ i โดยใช้สูตรต่อไปนี้:
\begin(สมการ)\เดลต้า A=\sum\limits_(j=1)^(n)a_(ij)A_(ij)=a_(i1)A_(i1)+a_(i2)A_(i2)+\ ldots+a_(ใน)A_(ใน) \end(สมการ)
อะนาล็อกของสูตรนี้มีอยู่ในคอลัมน์ด้วย สูตรสำหรับการขยายดีเทอร์มิแนนต์ในคอลัมน์ j มีดังนี้
\begin(สมการ)\เดลต้า A=\sum\limits_(i=1)^(n)a_(ij)A_(ij)=a_(1j)A_(1j)+a_(2j)A_(2j)+\ ldots+a_(nj)A_(nj) \end(สมการ)
กฎที่แสดงโดยสูตร (3) และ (4) มีการแสดงตัวอย่างโดยละเอียดและอธิบายไว้ในหัวข้อการลดลำดับของดีเทอร์มิแนนต์ การสลายตัวของดีเทอร์มิแนนต์ในแถว (คอลัมน์)
ให้เราระบุสูตรอื่นในการคำนวณดีเทอร์มิแนนต์ของเมทริกซ์สามเหลี่ยมบนและสามเหลี่ยมล่าง (สำหรับคำอธิบายคำศัพท์เหล่านี้ โปรดดูหัวข้อ "เมทริกซ์ ประเภทของเมทริกซ์ คำศัพท์พื้นฐาน") ดีเทอร์มิแนนต์ของเมทริกซ์ดังกล่าวเท่ากับผลคูณขององค์ประกอบบนเส้นทแยงมุมหลัก ตัวอย่าง:
\begin(ชิด) &\left| \begin(array) (cccc) 2 & -2 & 9 & 1 \\ 0 & 9 & 8 & 0 \\ 0 & 0 & 4 & -7 \\ 0 & 0 & 0 & -6 \end(อาร์เรย์) \right|= 2\cdot 9\cdot 4\cdot (-6)=-432.\\ &\left| \begin(array) (cccc) -3 & 0 & 0 & 0 \\ -5 & 0 & 0 & 0 \\ 8 & 2 & 1 & 0 \\ 5 & 4 & 0 & 10 \end(อาร์เรย์) \ ขวา|= -3\cdot 0\cdot 1 \cdot 10=0 \end(ชิด)
- ปล่อย titmouse ไปสู่ความตาย!
ปล่อยให้อิสรภาพโอบกอดเธอ!
แล้วเรือก็แล่นไป และเครื่องปฏิกรณ์ก็คำราม...
- Pash คุณดื้อเหรอ?
ฉันจำได้ว่าฉันไม่ชอบพีชคณิตจนกระทั่งเกรด 8 ฉันไม่ชอบมันเลย เธอทำให้ฉันโกรธ เพราะฉันไม่เข้าใจอะไรเลยที่นั่น
แล้วทุกอย่างก็เปลี่ยนไปเพราะฉันค้นพบเคล็ดลับอย่างหนึ่ง:
ในคณิตศาสตร์โดยทั่วไป (และโดยเฉพาะพีชคณิต) ทุกสิ่งถูกสร้างขึ้นบนระบบคำจำกัดความที่มีความสามารถและสม่ำเสมอ หากคุณรู้คำจำกัดความและเข้าใจแก่นแท้แล้ว ส่วนที่เหลือจะเข้าใจได้ไม่ยาก
หัวข้อบทเรียนวันนี้ก็เป็นเช่นนั้น เราจะพิจารณาประเด็นและคำจำกัดความที่เกี่ยวข้องโดยละเอียด ซึ่งคุณจะเข้าใจเมทริกซ์ ดีเทอร์มิแนนต์ และคุณสมบัติทั้งหมดทันทีและตลอดไป
ปัจจัยกำหนดเป็นแนวคิดหลักในพีชคณิตเมทริกซ์ เช่นเดียวกับสูตรคูณแบบย่อ พวกมันจะหลอกหลอนคุณตลอดหลักสูตรคณิตศาสตร์ชั้นสูง เราจึงอ่านดูและทำความเข้าใจอย่างละเอียด :)
และเราจะเริ่มต้นด้วยสิ่งที่ใกล้ชิดที่สุด - เมทริกซ์คืออะไร? และวิธีการทำงานอย่างถูกต้อง
ตำแหน่งที่ถูกต้องของดัชนีในเมทริกซ์
เมทริกซ์เป็นเพียงตารางที่เต็มไปด้วยตัวเลข นีโอไม่เกี่ยวอะไรด้วย
ลักษณะสำคัญอย่างหนึ่งของเมทริกซ์คือมิติของมันเช่น จำนวนแถวและคอลัมน์ที่ประกอบด้วย เรามักจะบอกว่าเมทริกซ์บางตัว $A$ มีขนาด $\left[ m\times n \right]$ ถ้าเมทริกซ์มีแถว $m$ และคอลัมน์ $n$ เขียนแบบนี้:
หรือเช่นนี้:
มีการกำหนดอื่นๆ - ทั้งหมดขึ้นอยู่กับความชอบของอาจารย์/ผู้สัมมนา/ผู้เขียนหนังสือเรียน แต่ไม่ว่าในกรณีใด ด้วย $\left[ m\times n \right]$ และ $((a)_(ij))$ ทั้งหมดนี้ ปัญหาเดียวกันก็เกิดขึ้น:
ดัชนีไหนรับผิดชอบอะไร? หมายเลขแถวมาก่อน แล้วตามด้วยหมายเลขคอลัมน์ใช่หรือไม่ หรือในทางกลับกัน?
เมื่ออ่านหนังสือบรรยายและตำราเรียน คำตอบจะชัดเจน แต่เมื่อในการสอบคุณมีเพียงกระดาษแผ่นเดียวที่มีงานอยู่ข้างหน้า คุณจะรู้สึกตื่นเต้นมากเกินไปและสับสนในทันใด
ดังนั้นเรามาแก้ไขปัญหานี้กันซักที ขั้นแรก เรามาจำระบบพิกัดปกติจากหลักสูตรคณิตศาสตร์ของโรงเรียนกันก่อน:
การแนะนำระบบพิกัดบนเครื่องบิน
จำเธอได้ไหม? มีจุดกำเนิด (จุด $O=\left(0;0 \right)$) ของแกน $x$ และ $y$ และแต่ละจุดบนระนาบถูกกำหนดโดยไม่ซ้ำกันโดยพิกัด: $A=\left( 1;2 \right)$, $B=\left(3;1 \right)$ ฯลฯ
ทีนี้ลองสร้างโครงสร้างนี้แล้ววางไว้ข้างเมทริกซ์เพื่อให้จุดกำเนิดของพิกัดอยู่ที่มุมซ้ายบน ทำไมต้องมี? ใช่ เพราะเมื่อเปิดหนังสือ เราจะเริ่มอ่านจากมุมซ้ายบนของหน้าอย่างแม่นยำ การจำสิ่งนี้เป็นเรื่องง่าย
แต่แกนควรหันไปทางไหน? เราจะชี้นำพวกเขาเพื่อให้ "หน้า" เสมือนทั้งหมดของเราถูกปกคลุมไปด้วยแกนเหล่านี้ จริงอยู่สำหรับสิ่งนี้ เราจะต้องหมุนระบบพิกัดของเรา ทางเลือกเดียวที่เป็นไปได้สำหรับข้อตกลงนี้คือ:
การซ้อนทับระบบพิกัดบนเมทริกซ์ ตอนนี้ทุกเซลล์ของเมทริกซ์มีพิกัดเฉพาะ $x$ และ $y$ ตัวอย่างเช่น การเขียน $((a)_(24))$ หมายความว่าเรากำลังเข้าถึงองค์ประกอบที่มีพิกัด $x=2$ และ $y=4$ ขนาดของเมทริกซ์ยังระบุด้วยตัวเลขคู่หนึ่งโดยเฉพาะ:
การกำหนดดัชนีในเมทริกซ์ เพียงแค่ดูภาพนี้อย่างระมัดระวัง ลองเล่นกับพิกัด (โดยเฉพาะเมื่อคุณทำงานกับเมทริกซ์จริงและปัจจัยกำหนด) - และในไม่ช้า คุณจะเข้าใจว่าแม้ในทฤษฎีบทและคำจำกัดความที่ซับซ้อนที่สุด คุณก็เข้าใจสิ่งที่กำลังพูดได้ดีอย่างสมบูรณ์แบบ
เข้าใจแล้ว? เรามาดูขั้นตอนแรกของการตรัสรู้กันดีกว่า - คำจำกัดความทางเรขาคณิตของดีเทอร์มิแนนต์ :)
คำจำกัดความทางเรขาคณิต
ก่อนอื่น ฉันอยากจะสังเกตว่าดีเทอร์มิแนนต์มีเฉพาะสำหรับเมทริกซ์จตุรัสในรูปแบบ $\left[ n\times n \right]$ เท่านั้น ดีเทอร์มิแนนต์คือตัวเลขที่คำนวณตามกฎเกณฑ์บางประการและเป็นหนึ่งในคุณลักษณะของเมทริกซ์นี้ (มีคุณสมบัติอื่นๆ: อันดับ เวกเตอร์ลักษณะเฉพาะ แต่มีมากกว่านั้นในบทเรียนอื่นๆ)
แล้วลักษณะนี้คืออะไร? มันหมายความว่าอะไร? มันง่ายมาก:
ดีเทอร์มีแนนต์ของเมทริกซ์จตุรัส $A=\left[ n\times n \right]$ คือปริมาตรของเส้นขนานในมิติ $n$ ซึ่งจะเกิดขึ้นถ้าเราพิจารณาแถวของเมทริกซ์เป็นเวกเตอร์ที่สร้างขอบของเส้นนี้ ขนานกัน
ตัวอย่างเช่น ดีเทอร์มิแนนต์ของเมทริกซ์ 2x2 เป็นเพียงพื้นที่ของสี่เหลี่ยมด้านขนาน แต่สำหรับเมทริกซ์ 3x3 นั้นเป็นปริมาตรของสี่เหลี่ยมด้านขนาน 3 มิติอยู่แล้วซึ่งเป็นปริมาตรเดียวกับที่ทำให้นักเรียนมัธยมปลายโกรธเคืองในบทเรียนสามมิติ .
เมื่อมองแวบแรก คำจำกัดความนี้อาจดูไม่เพียงพอโดยสิ้นเชิง แต่อย่าด่วนสรุป - ลองดูตัวอย่างกัน ในความเป็นจริงทุกอย่างเป็นเรื่องพื้นฐานวัตสัน:
งาน. ค้นหาปัจจัยกำหนดของเมทริกซ์:
\[\ซ้าย| \begin(เมทริกซ์) 1 & 0 \\ 0 & 3 \\\end(เมทริกซ์) \right|\quad \left| \begin(เมทริกซ์) 1 & -1 \\ 2 & 2 \\\end(เมทริกซ์) \right|\quad \left| \begin(เมทริกซ์)2 & 0 & 0 \\ 1 & 3 & 0 \\ 1 & 1 & 4 \\\end(เมทริกซ์) \right|\]
สารละลาย. ดีเทอร์มิแนนต์สองตัวแรกมีขนาด 2x2 พวกนี้ก็แค่พื้นที่ของสี่เหลี่ยมด้านขนาน ลองวาดพวกมันแล้วคำนวณพื้นที่กัน
สี่เหลี่ยมด้านขนานอันแรกสร้างจากเวกเตอร์ $((v)_(1))=\left(1;0 \right)$ และ $((v)_(2))=\left(0;3 \right) $:
ดีเทอร์มิแนนต์ของ 2x2 คือพื้นที่ของสี่เหลี่ยมด้านขนาน
แน่นอนว่านี่ไม่ใช่แค่สี่เหลี่ยมด้านขนาน แต่เป็นสี่เหลี่ยมมุมฉากด้วย พื้นที่ของมันคือ
สี่เหลี่ยมด้านขนานอันที่สองสร้างจากเวกเตอร์ $((v)_(1))=\left(1;-1 \right)$ และ $((v)_(2))=\left(2;2 \right )$ แล้วไงล่ะ? นี่คือสี่เหลี่ยมผืนผ้าด้วย:
ดีเทอร์มิแนนต์ 2x2 อีกอัน
ด้านข้างของสี่เหลี่ยมนี้ (โดยพื้นฐานแล้วคือความยาวของเวกเตอร์) คำนวณได้ง่ายๆ โดยใช้ทฤษฎีบทพีทาโกรัส:
\[\begin(align) & \left| ((v)_(1)) \right|=\sqrt(((1)^(2))+((\left(-1 \right))^(2)))=\sqrt(2); \\ & \ซ้าย| ((v)_(2)) \right|=\sqrt(((2)^(2))+((2)^(2)))=\sqrt(8)=2\sqrt(2); \\&S=\ซ้าย| ((v)_(1)) \right|\cdot \left| ((v)_(2)) \right|=\sqrt(2)\cdot 2\sqrt(2)=4 \\\end(จัดแนว)\]
ยังคงต้องจัดการกับปัจจัยสุดท้าย - มีเมทริกซ์ 3x3 อยู่แล้ว คุณจะต้องจำภาพสามมิติ:
ดีเทอร์มิแนนต์ของ 3x3 คือปริมาตรของเส้นขนาน
มันดูเหลือเชื่อ แต่จริงๆ แล้ว การจำสูตรปริมาตรของเส้นขนานก็เพียงพอแล้ว:
โดยที่ $S$ คือพื้นที่ของฐาน (ในกรณีของเรา นี่คือพื้นที่ของสี่เหลี่ยมด้านขนานบนระนาบ $OXY$) $h$ คือความสูงที่ลากไปยังฐานนี้ (อันที่จริงแล้ว $ z$-พิกัดของเวกเตอร์ $((v)_(3) )$)
พื้นที่ของสี่เหลี่ยมด้านขนาน (เราวาดแยกกัน) ก็คำนวณได้ง่ายเช่นกัน:
\[\begin(align) & S=2\cdot 3=6; \\ & V=S\cdot ชั่วโมง=6\cdot 4=24 \\\end(จัดแนว)\]
นั่นคือทั้งหมด! เราเขียนคำตอบ
คำตอบ: 3; 4; 24.
ข้อสังเกตเล็กๆ น้อยๆ เกี่ยวกับระบบสัญกรณ์ บางคนอาจจะไม่ชอบความจริงที่ว่าฉันเพิกเฉยต่อ "ลูกศร" เหนือเวกเตอร์ สมมุติว่าคุณสามารถสร้างความสับสนให้กับเวกเตอร์กับจุดหรืออย่างอื่นได้
แต่ขอจริงจังหน่อย: เราเป็นเด็กผู้ชายและเด็กผู้หญิงที่โตแล้ว ดังนั้นจากบริบทเราจึงเข้าใจได้ดีเมื่อเราพูดถึงเวกเตอร์และเมื่อเราพูดถึงประเด็นหนึ่งๆ ลูกศรเหล่านี้ขัดขวางการเล่าเรื่องเท่านั้น ซึ่งอัดแน่นไปด้วยสูตรทางคณิตศาสตร์แล้ว
และต่อไป. โดยหลักการแล้ว ไม่มีอะไรขัดขวางเราไม่ให้พิจารณาดีเทอร์มิแนนต์ของเมทริกซ์ขนาด 1x1 - เมทริกซ์ดังกล่าวเป็นเพียงเซลล์เดียว และตัวเลขที่เขียนในเซลล์นี้จะเป็นดีเทอร์มิแนนต์ แต่มีหมายเหตุสำคัญอยู่ที่นี่:
ต่างจากเล่มคลาสสิก ดีเทอร์มิแนนต์จะให้สิ่งที่เรียกว่า “ ปริมาณเชิง", เช่น. ปริมาตรโดยคำนึงถึงลำดับการพิจารณาเวกเตอร์แถว
และถ้าคุณต้องการได้ปริมาตรในความหมายคลาสสิกของคำ คุณจะต้องใช้โมดูลดีเทอร์มิแนนต์ แต่ตอนนี้ไม่จำเป็นต้องกังวลอีกต่อไป - อย่างไรก็ตามในไม่กี่วินาทีเราจะได้เรียนรู้วิธีคำนวณดีเทอร์มิแนนต์ใด ๆ พร้อมป้าย ขนาด ฯลฯ :)
นิยามพีชคณิต
เพื่อความสวยงามและความชัดเจนของวิธีการทางเรขาคณิต มีข้อเสียเปรียบอย่างมาก เนื่องจากไม่ได้บอกอะไรเราเกี่ยวกับวิธีคำนวณปัจจัยกำหนดนี้
ดังนั้นตอนนี้เราจะวิเคราะห์คำจำกัดความอื่น - พีชคณิต เพื่อที่จะทำสิ่งนี้ เราจำเป็นต้องมีการเตรียมการทางทฤษฎีสั้นๆ แต่ในตอนท้าย เราจะได้เครื่องมือที่ช่วยให้เราสามารถคำนวณอะไรก็ได้ที่เราต้องการในเมทริกซ์
จริงอยู่ที่ปัญหาใหม่จะปรากฏขึ้นที่นั่น... แต่สิ่งแรกต้องมาก่อน
การเรียงสับเปลี่ยนและการผกผัน
ลองเขียนตัวเลขตั้งแต่ 1 ถึง $n$ ในบรรทัด คุณจะได้รับสิ่งนี้:
ทีนี้ (เพื่อความสนุก) เรามาสลับตัวเลขกัน คุณสามารถเปลี่ยนสิ่งที่อยู่ใกล้เคียงได้:
หรือบางที - ไม่ใกล้เคียงเป็นพิเศษ:
และเดาอะไร? ไม่มีอะไร! ในพีชคณิตเรื่องไร้สาระนี้เรียกว่าการเรียงสับเปลี่ยน และก็มีคุณสมบัติมากมาย
คำนิยาม. การเรียงสับเปลี่ยนความยาว $n$ คือสตริงที่มีตัวเลขต่างกัน $n$ ซึ่งเขียนตามลำดับใดก็ได้ โดยปกติแล้ว เราจะพิจารณาจำนวนธรรมชาติ $n$ ตัวแรก (เช่น แค่ตัวเลข 1, 2, ..., $n$) จากนั้นจึงผสมกันเพื่อให้ได้การเรียงสับเปลี่ยนที่ต้องการ
การเรียงสับเปลี่ยนจะแสดงในลักษณะเดียวกับเวกเตอร์ - เพียงแค่ตัวอักษรและรายการองค์ประกอบตามลำดับในวงเล็บ ตัวอย่างเช่น: $p=\left(1;3;2 \right)$ หรือ $p=\left(2;5;1;4;3 \right)$ จดหมายจะเป็นอะไรก็ได้ แต่ให้เป็น $p$ :)
นอกจากนี้ เพื่อความเรียบง่ายในการนำเสนอ เราจะใช้การเรียงสับเปลี่ยนความยาว 5 ซึ่งมีความร้ายแรงพอที่จะสังเกตเห็นผลกระทบที่น่าสงสัย แต่ยังไม่รุนแรงเท่ากับสมองที่เปราะบางเท่ากับการเรียงสับเปลี่ยนความยาว 6 ขึ้นไป นี่คือตัวอย่างของการเรียงสับเปลี่ยนดังกล่าว:
\[\begin(align) & ((p)_(1))=\left(1;2;3;4;5 \right) \\ & ((p)_(2))=\left(1 ;3;2;5;4 \right) \\ & ((p)_(3))=\left(5;4;3;2;1 \right) \\\end(align)\]
โดยธรรมชาติแล้ว การเรียงสับเปลี่ยนความยาว $n$ ถือได้ว่าเป็นฟังก์ชันที่กำหนดไว้บนเซต $\left\( 1;2;...;n \right\)$ และจับคู่เซตนี้เข้ากับตัวมันเองโดยปริยาย เมื่อย้อนกลับไปที่การเรียงสับเปลี่ยนที่เพิ่งเขียนลงไป $((p)_(1))$, $((p)_(2))$ และ $((p)_(3))$ เราสามารถเขียนได้อย่างถูกกฎหมาย:
\[((p)_(1))\left(1 \right)=1;((p)_(2))\left(3 \right)=2;((p)_(3))\ ซ้าย(2 \right)=4;\]
จำนวนการเรียงสับเปลี่ยนความยาว $n$ นั้นมีจำกัดเสมอและเท่ากับ $n!$ - นี่เป็นข้อเท็จจริงที่พิสูจน์ได้ง่ายจากการใช้สูตรเชิงผสม ตัวอย่างเช่น หากเราต้องการเขียนการเรียงสับเปลี่ยนความยาว 5 ทั้งหมด เราจะลังเลมาก เนื่องจากจะมีการเรียงสับเปลี่ยนเช่นนั้น
ลักษณะสำคัญอย่างหนึ่งของการเรียงสับเปลี่ยนคือจำนวนการผกผันในนั้น
คำนิยาม. การผกผันในการเรียงสับเปลี่ยน $p=\left(((a)_(1));((a)_(2));...;((a)_(n)) \right)$ — คู่ใดๆ $ \left(((a)_(i));((a)_(j)) \right)$ ดังนั้น $i \lt j$ แต่ $((a)_(i)) \gt ( (ก)_(เจ))$. พูดง่ายๆ ก็คือ การผกผันคือเมื่อตัวเลขที่มากกว่าอยู่ทางด้านซ้ายของจำนวนที่น้อยกว่า (ไม่จำเป็นต้องเป็นเพื่อนบ้าน)
เราจะแสดงด้วย $N\left(p \right)$ จำนวนของการกลับรายการในการเรียงสับเปลี่ยน $p$ แต่เตรียมพร้อมที่จะเผชิญกับสัญลักษณ์อื่นๆ ในตำราเรียนและผู้แต่งที่แตกต่างกัน - ไม่มีมาตรฐานที่เหมือนกันที่นี่ หัวข้อของการผกผันนั้นกว้างขวางมากและจะมีการเน้นบทเรียนแยกต่างหาก ตอนนี้งานของเราคือเพียงเรียนรู้วิธีนับพวกมันในปัญหาจริง
ตัวอย่างเช่น ลองนับจำนวนการกลับด้านในการเรียงสับเปลี่ยน $p=\left(1;4;5;3;2 \right)$:
\[\left(4;3 \right);\left(4;2 \right);\left(5;3 \right);\left(5;2 \right);\left(3;2 \right ).\]
ดังนั้น $N\left(p \right)=5$ อย่างที่คุณเห็นไม่มีอะไรผิดปกติกับเรื่องนี้ ฉันจะพูดทันที: จากนี้ไปเราจะไม่สนใจตัวเลข $N\left(p \right)$ มากนัก แต่จะสนใจในเรื่องความสมดุล/ความคี่ของมัน และที่นี่เราจะก้าวไปสู่คำศัพท์สำคัญของบทเรียนวันนี้อย่างราบรื่น
อะไรเป็นตัวกำหนด
ให้เมทริกซ์จตุรัส $A=\left[ n\times n \right]$ ถูกกำหนดไว้ แล้ว:
คำนิยาม. ดีเทอร์มิแนนต์ของเมทริกซ์ $A=\left[ n\times n \right]$ คือผลรวมพีชคณิตของเงื่อนไข $n!$ ที่ประกอบขึ้นดังนี้ แต่ละเทอมเป็นผลคูณขององค์ประกอบเมทริกซ์ $n$ ซึ่งนำมาหนึ่งรายการจากแต่ละแถวและแต่ละคอลัมน์ คูณด้วย (−1) ยกกำลังของจำนวนการผกผัน:
\[\ซ้าย| A\right|=\sum\limits_(n{{{\left(-1 \right)}^{N\left(p \right)}}\cdot {{a}_{1;p\left(1 \right)}}\cdot {{a}_{2;p\left(2 \right)}}\cdot ...\cdot {{a}_{n;p\left(n \right)}}}\]!}
จุดพื้นฐานในการเลือกปัจจัยสำหรับแต่ละเทอมในตัวกำหนดคือข้อเท็จจริงที่ว่าไม่มีปัจจัยสองตัวปรากฏในแถวเดียวกันหรือในคอลัมน์เดียวกัน
ด้วยเหตุนี้ เราจึงสามารถสรุปได้โดยไม่สูญเสียความทั่วไปที่ว่าดัชนี $i$ ของปัจจัย $((a)_(i;j))$ “วิ่งผ่าน” ค่า 1, ..., $n$ และดัชนี $j$ เป็นการเรียงสับเปลี่ยนของค่าแรก:
และเมื่อมีการเรียงสับเปลี่ยน $p$ เราสามารถคำนวณการกลับด้าน $N\left(p \right)$ ได้อย่างง่ายดาย และเทอมถัดไปของดีเทอร์มิแนนต์ก็พร้อมแล้ว
โดยธรรมชาติแล้วไม่มีใครห้ามการแลกเปลี่ยนปัจจัยในระยะใด ๆ (หรือในทั้งหมดพร้อมกัน - ทำไมต้องเสียเวลากับเรื่องมโนสาเร่?) จากนั้นดัชนีแรกก็จะแสดงถึงการจัดเรียงใหม่ด้วย แต่ท้ายที่สุดแล้ว จะไม่มีอะไรเปลี่ยนแปลง: จำนวนการผกผันทั้งหมดในดัชนี $i$ และ $j$ ยังคงความเท่าเทียมกันภายใต้การบิดเบือนดังกล่าว ซึ่งค่อนข้างสอดคล้องกับกฎเก่าที่ดี:
การจัดเรียงตัวประกอบใหม่จะไม่เปลี่ยนผลคูณของตัวเลข
เพียงแต่อย่าแนบกฎนี้กับการคูณเมทริกซ์ ไม่เหมือนการคูณตัวเลข ตรงที่ไม่สามารถสับเปลี่ยนได้ แต่ฉันพูดนอกเรื่อง :)
เมทริกซ์ 2x2
ในความเป็นจริง คุณยังสามารถพิจารณาเมทริกซ์ขนาด 1x1 ได้ด้วย ซึ่งจะเป็นเซลล์เดียว และดีเทอร์มิแนนต์ของมันจะเท่ากับจำนวนที่เขียนในเซลล์นี้ ดังที่คุณอาจเดาได้ ไม่มีอะไรน่าสนใจ.
ลองพิจารณาเมทริกซ์จตุรัสขนาด 2x2 กัน:
\[\left[ \begin(เมทริกซ์) ((a)_(11)) & ((a)_(12)) \\ ((a)_(21)) & ((a)_(22)) \\\end(เมทริกซ์) \right]\]
เนื่องจากจำนวนบรรทัดในนั้นคือ $n=2$ ดีเทอร์มิแนนต์จะมีเงื่อนไข $n!=2!=1\cdot 2=2$ มาเขียนกัน:
\[\begin(align) & ((\left(-1 \right))^(N\left(1;2 \right)))\cdot ((a)_(11))\cdot ((a) _(22))=((\left(-1 \right))^(0))\cdot ((a)_(11))\cdot ((a)_(22))=((a)_ (11))((ก)_(22)); \\ & ((\left(-1 \right))^(N\left(2;1 \right)))\cdot ((a)_(12))\cdot ((a)_(21)) =((\left(-1 \right))^(1))\cdot ((a)_(12))\cdot ((a)_(21))=((a)_(12))( (ก)_(21)) \\\end(จัดแนว)\]
แน่นอนว่าในการเรียงสับเปลี่ยน $\left(1;2 \right)$ ประกอบด้วยสององค์ประกอบ จะไม่มีการกลับด้าน ดังนั้น $N\left(1;2 \right)=0$ แต่ในการเรียงสับเปลี่ยน $\left(2;1 \right)$ มีการผกผันหนึ่งครั้ง (อันที่จริง 2< 1), поэтому $N\left(2;1 \right)=1.$
โดยรวมแล้ว สูตรสากลสำหรับการคำนวณดีเทอร์มิแนนต์สำหรับเมทริกซ์ 2x2 มีลักษณะดังนี้:
\[\ซ้าย| \begin(เมทริกซ์) ((a)_(11)) & ((a)_(12)) \\ ((a)_(21)) & ((a)_(22)) \\\end( เมทริกซ์) \right|=((a)_(11))((a)_(22))-((a)_(12))((a)_(21))\]
ในเชิงกราฟิก สิ่งนี้สามารถแสดงเป็นผลคูณขององค์ประกอบบนเส้นทแยงมุมหลัก ลบด้วยผลคูณขององค์ประกอบบนเส้นทแยงมุมด้านข้าง:
ดีเทอร์มิแนนต์ของเมทริกซ์ 2x2 ลองดูตัวอย่างบางส่วน:
\[\ซ้าย| \begin(เมทริกซ์) 5 & 6 \\ 8 & 9 \\\end(เมทริกซ์) \right|;\quad \left| \begin(เมทริกซ์) 7 & 12 \\ 14 & 1 \\\end(เมทริกซ์) \right|.\]
สารละลาย. ทุกอย่างถูกนับในบรรทัดเดียว เมทริกซ์แรก:
และประการที่สอง:
คำตอบ: −3; −161.
อย่างไรก็ตาม มันง่ายเกินไป ลองดูเมทริกซ์ 3x3 กัน - มันน่าสนใจอยู่แล้ว
เมทริกซ์ 3x3
พิจารณาเมทริกซ์จตุรัส 3x3:
\[\left[ \begin(เมทริกซ์) ((a)_(11)) & ((a)_(12)) & ((a)_(13)) \\ ((a)_(21)) & ((a)_(22)) & ((a)_(23)) \\ ((a)_(31)) & ((a)_(32)) & ((a)_(33) ) \\\end(เมทริกซ์) \right]\]
เมื่อคำนวณดีเทอร์มิแนนต์ เราจะได้ $3!=1\cdot 2\cdot 3=6$ เทอม - ไม่มากเกินไปจนต้องตกใจ แต่ก็เพียงพอที่จะเริ่มมองหารูปแบบบางอย่าง ขั้นแรก เรามาเขียนการเรียงสับเปลี่ยนขององค์ประกอบทั้งสามทั้งหมดแล้วนับการผกผันในแต่ละองค์ประกอบ:
\[\begin(align) & ((p)_(1))=\left(1;2;3 \right)\ลูกศรขวา N\left(((p)_(1)) \right)=N\ ซ้าย(1;2;3 \right)=0; \\ & ((p)_(2))=\left(1;3;2 \right)\ลูกศรขวา N\left(((p)_(2)) \right)=N\left(1;3 ;2 \ขวา)=1; \\ & ((p)_(3))=\left(2;1;3 \right)\ลูกศรขวา N\left(((p)_(3)) \right)=N\left(2;1 ;3 \ขวา)=1; \\ & ((p)_(4))=\left(2;3;1 \right)\ลูกศรขวา N\left(((p)_(4)) \right)=N\left(2;3 ;1 \ขวา)=2; \\ & ((p)_(5))=\left(3;1;2 \right)\ลูกศรขวา N\left(((p)_(5)) \right)=N\left(3;1 ;2 \ขวา)=2; \\ & ((p)_(6))=\left(3;2;1 \right)\ลูกศรขวา N\left(((p)_(6)) \right)=N\left(3;2 ;1 \ขวา)=3. \\\end(จัดแนว)\]
ตามที่คาดไว้ มีการเรียงสับเปลี่ยนทั้งหมด 6 วิธีถูกเขียนออกมา: $((p)_(1))$, ... $((p)_(6))$ (โดยปกติแล้ว มันเป็นไปได้ที่จะเขียนออกมาเป็น ลำดับที่แตกต่างกัน - สิ่งนี้ไม่มีความแตกต่างใด ๆ ที่จะเปลี่ยนแปลง) และจำนวนการกลับรายการจะแตกต่างกันไปตั้งแต่ 0 ถึง 3
โดยทั่วไป เราจะมีคำศัพท์สามคำที่มี "บวก" (โดยที่ $N\left(p \right)$ เป็นเลขคู่) และอีกสามคำที่มี "ลบ" โดยทั่วไป ดีเทอร์มิแนนต์จะคำนวณตามสูตร:
\[\ซ้าย| \begin(เมทริกซ์) ((a)_(11)) & ((a)_(12)) & ((a)_(13)) \\ ((a)_(21)) & ((a) _(22)) & ((a)_(23)) \\ ((a)_(31)) & ((a)_(32)) & ((a)_(33)) \\\end (เมทริกซ์) \right|=\begin(เมทริกซ์) ((a)_(11))((a)_(22))((a)_(33))+((a)_(12))( (a)_(23))((a)_(31))+((a)_(13))((a)_(21))((a)_(32))- \\ -( (ก)_(13))((ก)_(22))((ก)_(31))-((ก)_(12))((ก)_(21))((ก)_ (33))-((a)_(11))((a)_(23))((a)_(32)) \\\end(เมทริกซ์)\]
อย่าเพิ่งนั่งลงแล้วอัดดัชนีเหล่านี้ทั้งหมดอย่างเกรี้ยวกราดตอนนี้! แทนที่จะเป็นตัวเลขที่เข้าใจยาก ควรจำกฎช่วยในการจำต่อไปนี้:
กฎสามเหลี่ยม. ในการค้นหาดีเทอร์มิแนนต์ของเมทริกซ์ 3x3 คุณต้องเพิ่มผลคูณสามขององค์ประกอบที่อยู่บนเส้นทแยงมุมหลักและที่จุดยอดของสามเหลี่ยมหน้าจั่วที่มีด้านขนานกับเส้นทแยงมุมนี้ จากนั้นลบผลคูณทั้งสามที่เหมือนกัน แต่อยู่บนเส้นทแยงมุมรอง . แผนผังมีลักษณะดังนี้:
ปัจจัยกำหนดของเมทริกซ์ 3x3: กฎสามเหลี่ยม
สามเหลี่ยมเหล่านี้ (หรือรูปดาวห้าแฉก แล้วแต่คุณต้องการ) ที่ผู้คนชอบวาดลงในหนังสือเรียนและคู่มือพีชคณิตทุกประเภท อย่างไรก็ตาม อย่าพูดถึงเรื่องน่าเศร้าเลย มาคำนวณปัจจัยที่กำหนดกันดีกว่า - เพื่ออุ่นเครื่องก่อนสิ่งที่ยากจริงๆ :)
งาน. คำนวณปัจจัยกำหนด:
\[\ซ้าย| \begin(เมทริกซ์) 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 1 \\\end(เมทริกซ์) \right|\]
สารละลาย. เราทำงานตามกฎของสามเหลี่ยม ขั้นแรก ลองนับคำศัพท์สามคำที่ประกอบด้วยองค์ประกอบบนเส้นทแยงมุมหลักและขนานไปกับมัน:
\[\begin(จัดตำแหน่ง) & 1\cdot 5\cdot 1+2\cdot 6\cdot 7+3\cdot 4\cdot 8= \\ & =5+84+96=185 \\\end(จัดตำแหน่ง) \]
ทีนี้มาดูเส้นทแยงมุมด้านข้าง:
\[\begin(จัดแนว) & 3\cdot 5\cdot 7+2\cdot 4\cdot 1+1\cdot 6\cdot 8= \\ & =105+8+48=161 \\\end(จัดแนว) \]
สิ่งที่เหลืออยู่คือการลบวินาทีจากตัวเลขแรก - แล้วเราจะได้คำตอบ:
นั่นคือทั้งหมด!
อย่างไรก็ตาม ปัจจัยกำหนดของเมทริกซ์ 3x3 ยังไม่ใช่จุดสุดยอดของทักษะ สิ่งที่น่าสนใจที่สุดรอเราอยู่ต่อไป :)
รูปแบบทั่วไปสำหรับการคำนวณปัจจัยกำหนด
ดังที่เราทราบ เมื่อมิติเมทริกซ์ $n$ เพิ่มขึ้น จำนวนพจน์ในดีเทอร์มิแนนต์จะเป็น $n!$ และจะเพิ่มขึ้นอย่างรวดเร็ว ถึงกระนั้น factorial ก็ไม่ใช่เรื่องไร้สาระ มันเป็นฟังก์ชันที่เติบโตอย่างรวดเร็ว
สำหรับเมทริกซ์ 4x4 แล้ว การนับดีเทอร์มิแนนต์โดยตรง (เช่น ผ่านการเรียงสับเปลี่ยน) จะไม่ค่อยดีนัก โดยทั่วไปฉันจะเงียบประมาณ 5x5 และมากกว่านั้น ดังนั้นคุณสมบัติบางอย่างของดีเทอร์มิแนนต์จึงเข้ามามีบทบาท แต่การทำความเข้าใจคุณสมบัติเหล่านี้จำเป็นต้องมีการเตรียมทางทฤษฎีเล็กน้อย
พร้อม? ไป!
เมทริกซ์ไมเนอร์คืออะไร?
ให้เมทริกซ์ใดๆ $A=\left[ m\times n \right]$ มอบให้ หมายเหตุ: ไม่จำเป็นต้องเป็นรูปสี่เหลี่ยมจัตุรัส ต่างจากดีเทอร์มิแนนต์ตรงที่ผู้เยาว์เป็นสิ่งที่น่ารักซึ่งไม่เพียงมีอยู่ในเมทริกซ์จัตุรัสที่รุนแรงเท่านั้น ให้เราเลือกหลายแถวและคอลัมน์ (เช่น $k$) ในเมทริกซ์นี้ โดยมี $1\le k\le m$ และ $1\le k\le n$ แล้ว:
คำนิยาม. อันดับรอง $k$ คือดีเทอร์มิแนนต์ของเมทริกซ์จตุรัสที่เกิดขึ้นที่จุดตัดของคอลัมน์และแถว $k$ ที่เลือก เราจะเรียกเมทริกซ์ใหม่นี้ว่าเมทริกซ์รองด้วย
ผู้เยาว์ดังกล่าวจะแสดงด้วย $((M)_(k))$ โดยธรรมชาติแล้ว เมทริกซ์ตัวหนึ่งสามารถมีลำดับรอง $k$ ได้ทั้งหมด นี่คือตัวอย่างของลำดับรอง 2 สำหรับเมทริกซ์ $\left[ 5\times 6 \right]$:
การเลือก $k = 2$ คอลัมน์และแถวเพื่อสร้างรายย่อย
ไม่จำเป็นเลยที่แถวและคอลัมน์ที่เลือกจะอยู่ติดกันดังในตัวอย่างที่อธิบายไว้ สิ่งสำคัญคือจำนวนแถวและคอลัมน์ที่เลือกเท่ากัน (นี่คือตัวเลข $k$)
มีอีกคำจำกัดความหนึ่ง บางทีบางคนอาจจะชอบมันมากกว่านี้:
คำนิยาม. ให้เมทริกซ์สี่เหลี่ยม $A=\left[ m\times n \right]$ ถูกกำหนดไว้ หลังจากลบหนึ่งคอลัมน์ขึ้นไปและหนึ่งแถวขึ้นไป ถ้าเมทริกซ์จตุรัสขนาด $\left[ k\times k \right]$ ถูกสร้างขึ้น ดังนั้นดีเทอร์มิแนนต์ของมันคือค่ารอง $((M)_(k)) $ . บางครั้งเราจะเรียกเมทริกซ์นั้นว่าไมเนอร์ - สิ่งนี้จะชัดเจนจากบริบท
อย่างที่แมวของฉันบอก บางครั้งการกลับมาจากชั้น 11 เพื่อกินอาหารยังดีกว่าการนั่งร้องเหมียวอยู่บนระเบียง
ตัวอย่าง. ให้เมทริกซ์ได้รับ
เมื่อเลือกแถว 1 และคอลัมน์ 2 เราจะได้ลำดับรองอันดับหนึ่ง:
\[((M)_(1))=\ซ้าย| 7\ขวา|=7\]
โดยการเลือกแถว 2, 3 และคอลัมน์ 3, 4 เราจะได้ลำดับรองอันดับสอง:
\[((M)_(2))=\ซ้าย| \begin(เมทริกซ์) 5 & 3 \\ 6 & 1 \\\end(เมทริกซ์) \right|=5-18=-13\]
และหากคุณเลือกทั้งสามแถวรวมถึงคอลัมน์ 1, 2, 4 จะมีลำดับรองที่สาม:
\[((M)_(3))=\ซ้าย| \begin(เมทริกซ์) 1 & 7 & 0 \\ 2 & 4 & 3 \\ 3 & 0 & 1 \\\end(เมทริกซ์) \right|\]
ผู้อ่านจะค้นหาผู้เยาว์รายอื่นที่มีคำสั่งซื้อ 1, 2 หรือ 3 ได้ไม่ยาก ดังนั้นเราจึงเดินหน้าต่อไป
การบวกพีชคณิต
“เอาล่ะ มินเนี่ยนตัวน้อยเหล่านี้ให้อะไรเราบ้าง” - คุณอาจจะถาม ด้วยตัวเอง - ไม่มีอะไร แต่ในเมทริกซ์จตุรัส ผู้เยาว์แต่ละคนมี "สหาย" - ผู้เยาว์เพิ่มเติม เช่นเดียวกับส่วนเสริมพีชคณิต และเทคนิคทั้งสองนี้จะทำให้เราสามารถแยกปัจจัยกำหนดได้เหมือนถั่ว
คำนิยาม. ให้เมทริกซ์จัตุรัส $A=\left[ n\times n \right]$ ถูกกำหนด โดยเลือก $((M)_(k))$ รองไว้ จากนั้น ตัวรองเพิ่มเติมสำหรับตัวรอง $((M)_(k))$ เป็นส่วนหนึ่งของเมทริกซ์ดั้งเดิม $A$ ซึ่งจะยังคงอยู่หลังจากลบแถวและคอลัมน์ทั้งหมดที่เกี่ยวข้องกับการเขียนตัวรอง $((M)_ (ฎ))$:
เพิ่มเติมรายย่อยถึงรายย่อย $((M)_(2))$
ขอให้เราชี้แจงประเด็นหนึ่ง: รายย่อยเพิ่มเติมไม่ได้เป็นเพียง "ชิ้นส่วนของเมทริกซ์" แต่เป็นปัจจัยกำหนดของชิ้นส่วนนี้
ผู้เยาว์เพิ่มเติมจะมีเครื่องหมายดอกจันกำกับ: $M_(k)^(*)$:
โดยที่การดำเนินการ $A\nabla ((M)_(k))$ หมายถึง "ลบแถวและคอลัมน์ที่รวมอยู่ใน $(M)_(k))$" ออกจาก $A$ การดำเนินการนี้ไม่เป็นที่ยอมรับโดยทั่วไปในวิชาคณิตศาสตร์ - ฉันเพิ่งคิดค้นมันเองเพื่อความสวยงามของเรื่องราว :)
ผู้เยาว์เพิ่มเติมไม่ค่อยได้ใช้ด้วยตัวเอง เป็นส่วนหนึ่งของโครงสร้างที่ซับซ้อนมากขึ้น - ส่วนเสริมพีชคณิต
คำนิยาม. ส่วนเสริมพีชคณิตของ $((M)_(k))$ รอง $M_(k)^(*)$ เพิ่มเติมคูณด้วยค่า $((\left(-1 \right))^(S ))$ โดยที่ $S$ คือผลรวมของจำนวนแถวและคอลัมน์ทั้งหมดที่เกี่ยวข้องกับตัวรองดั้งเดิม $((M)_(k))$
ตามกฎแล้ว ส่วนเสริมพีชคณิตของ $((M)_(k))$ รองจะเขียนแทนด้วย $((A)_(k))$ นั่นเป็นเหตุผล:
\[((A)_(k))=((\left(-1 \right))^(S))\cdot M_(k)^(*)\]
ยาก? เมื่อมองแวบแรกใช่ แต่มันก็ไม่แน่ เพราะในความเป็นจริงทุกอย่างเป็นเรื่องง่าย ลองดูตัวอย่าง:
ตัวอย่าง. รับเมทริกซ์ 4x4:
มาเลือกลำดับรองรองกัน
\[((M)_(2))=\ซ้าย| \begin(เมทริกซ์) 3 & 4 \\ 15 & 16 \\\end(เมทริกซ์) \right|\]
Captain Obviousness ดูเหมือนจะบอกเป็นนัยกับเราว่าเมื่อรวบรวมผู้เยาว์นี้ บรรทัดที่ 1 และ 4 รวมถึงคอลัมน์ 3 และ 4 เกี่ยวข้อง ขีดฆ่าพวกเขาออกแล้วเราจะได้ผู้เยาว์เพิ่มเติม:
ยังคงต้องหาตัวเลข $S$ และรับส่วนเสริมพีชคณิต เนื่องจากเราทราบจำนวนแถว (1 และ 4) และคอลัมน์ (3 และ 4) ที่เกี่ยวข้อง ทุกอย่างจึงเป็นเรื่องง่าย:
\[\begin(จัดแนว) & S=1+4+3+4=12; \\ & ((A)_(2))=((\left(-1 \right))^(S))\cdot M_(2)^(*)=((\left(-1 \right) )^(12))\cdot \left(-4 \right)=-4\end(align)\]
คำตอบ: $((A)_(2))=-4$
นั่นคือทั้งหมด! ในความเป็นจริงความแตกต่างทั้งหมดระหว่างส่วนเสริมย่อยเพิ่มเติมและส่วนเสริมพีชคณิตนั้นอยู่ที่เครื่องหมายลบที่ด้านหน้าเท่านั้นและก็ไม่เสมอไปด้วยซ้ำ
ทฤษฎีบทของลาปลาซ
แล้วเราก็มาถึงจุดที่ที่จริงแล้ว จริงๆ แล้ว ตัวรองและการบวกพีชคณิตทั้งหมดนี้จำเป็น
ทฤษฎีบทของลาปลาซเรื่องการสลายตัวของดีเทอร์มิแนนต์ ให้ $k$ แถว (คอลัมน์) ถูกเลือกในเมทริกซ์ขนาด $\left[ n\times n \right]$ โดยมี $1\le k\le n-1$ จากนั้นดีเทอร์มิแนนต์ของเมทริกซ์นี้จะเท่ากับผลรวมของผลิตภัณฑ์ทั้งหมดของลำดับรอง $k$ ที่มีอยู่ในแถวที่เลือก (คอลัมน์) และการเสริมพีชคณิต:
\[\ซ้าย| A \right|=\sum(((M)_(k))\cdot ((A)_(k)))\]
ยิ่งไปกว่านั้น จะมี $C_(n)^(k)$ ของข้อกำหนดดังกล่าวทุกประการ
โอเค โอเค: ประมาณ $C_(n)^(k)$ - ฉันได้แสดงไปแล้ว ไม่มีอะไรแบบนั้นในทฤษฎีบทดั้งเดิมของ Laplace แต่ไม่มีใครยกเลิก Combinatorics และการดูเงื่อนไขอย่างรวดเร็วจะช่วยให้คุณเห็นด้วยตัวเองว่าจะมีเงื่อนไขมากมายขนาดนั้น :)
เราจะไม่พิสูจน์มัน แม้ว่าจะไม่ได้นำเสนอความยากลำบากใดๆ ก็ตาม แต่การคำนวณทั้งหมดขึ้นอยู่กับการเรียงสับเปลี่ยนแบบเก่าที่ดี และการกลับเลขคู่/คี่ อย่างไรก็ตาม หลักฐานจะถูกนำเสนอในย่อหน้าแยกต่างหาก และวันนี้ เรามีบทเรียนเชิงปฏิบัติล้วนๆ
ดังนั้นเราจึงไปยังกรณีพิเศษของทฤษฎีบทนี้ เมื่อเซลล์รองคือเซลล์แต่ละเซลล์ของเมทริกซ์
การสลายตัวของดีเทอร์มิแนนต์ในแถวและคอลัมน์
สิ่งที่เราจะพูดถึงตอนนี้คือเครื่องมือหลักในการทำงานกับดีเทอร์มิแนนต์อย่างแม่นยำ เพื่อประโยชน์ของการเริ่มต้นเรื่องไร้สาระทั้งหมดที่มีการเรียงสับเปลี่ยน การรอง และการบวกพีชคณิต
อ่านและสนุก:
ข้อพิสูจน์ของทฤษฎีบทของลาปลาซ (การสลายตัวของดีเทอร์มิแนนต์ในแถว/คอลัมน์) ให้เลือกหนึ่งแถวในเมทริกซ์ขนาด $\left[ n\times n \right]$ ผู้เยาว์ในบรรทัดนี้จะเป็น $n$ แต่ละเซลล์:
\[((M)_(1))=((a)_(ij)),\quad j=1,...,n\]
ตัวรองเพิ่มเติมนั้นง่ายต่อการคำนวณ เพียงใช้เมทริกซ์ดั้งเดิมแล้วขีดฆ่าแถวและคอลัมน์ที่มี $((a)_(ij))$ ลองเรียกผู้เยาว์ดังกล่าวว่า $M_(ij)^(*)$
สำหรับการเสริมพีชคณิต เรายังต้องการตัวเลข $S$ แต่ในกรณีของลำดับรอง 1 มันเป็นเพียงผลรวมของ "พิกัด" ของเซลล์ $((a)_(ij))$:
จากนั้นดีเทอร์มิแนนต์ดั้งเดิมสามารถเขียนได้ในรูปของ $((a)_(ij))$ และ $M_(ij)^(*)$ ตามทฤษฎีบทของ Laplace:
\[\ซ้าย| A \right|=\sum\limits_(j=1)^(n)(((a)_(ij))\cdot ((\left(-1 \right))^(i+j))\cdot ((ม)_(ij)))\]
นั่นคือสิ่งที่มันเป็น สูตรสลายดีเทอร์มิแนนต์เป็นแถว. แต่เช่นเดียวกันกับคอลัมน์
ผลที่ตามมานี้สามารถสรุปได้หลายประการทันที:
- โครงร่างนี้ใช้ได้ดีพอๆ กันสำหรับทั้งแถวและคอลัมน์ ในความเป็นจริง ส่วนใหญ่แล้วการสลายตัวจะเกิดขึ้นอย่างแม่นยำตามคอลัมน์มากกว่าตามแถว
- จำนวนพจน์ในส่วนขยายจะเป็น $n$ ทุกประการเสมอ ซึ่งน้อยกว่า $C_(n)^(k)$ อย่างมาก และยิ่งกว่านั้นอีก $n!$
- แทนที่จะพิจารณาปัจจัยกำหนดเพียงตัวเดียว $\left[ n\times n \right]$ คุณจะต้องพิจารณาปัจจัยกำหนดหลายตัวที่มีขนาดน้อยกว่าหนึ่งตัว: $\left[ \left(n-1 \right)\times \left(n-1 \ ขวา) \right ]$
ข้อเท็จจริงสุดท้ายมีความสำคัญอย่างยิ่ง ตัวอย่างเช่นแทนที่จะเป็นดีเทอร์มิแนนต์ 4x4 ที่โหดร้ายตอนนี้ก็เพียงพอแล้วที่จะนับดีเทอร์มิแนนต์ 3x3 หลายตัว - เราจะจัดการกับพวกมันอย่างไร :)
งาน. ค้นหาปัจจัยกำหนด:
\[\ซ้าย| \begin(เมทริกซ์) 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\\end(เมทริกซ์) \right|\]
สารละลาย. มาขยายดีเทอร์มิแนนต์นี้ตามบรรทัดแรก:
\[\begin(align) \left| A \right|=1\cdot ((\left(-1 \right))^(1+1))\cdot \left| \begin(เมทริกซ์) 5 & 6 \\ 8 & 9 \\\end(เมทริกซ์) \right|+ & \\ 2\cdot ((\left(-1 \right))^(1+2))\cdot \ซ้าย| \begin(เมทริกซ์) 4 & 6 \\ 7 & 9 \\\end(เมทริกซ์) \right|+ & \\ 3\cdot ((\left(-1 \right))^(1+3))\cdot \ซ้าย| \begin(เมทริกซ์) 4 & 5 \\ 7 & 8 \\\end(เมทริกซ์) \right|= & \\\end(align)\]
\[\begin(align) & =1\cdot \left(45-48 \right)-2\cdot \left(36-42 \right)+3\cdot \left(32-35 \right)= \\ & =1\cdot \left(-3 \right)-2\cdot \left(-6 \right)+3\cdot \left(-3 \right)=0 \\\end(จัดแนว)\]
งาน. ค้นหาปัจจัยกำหนด:
\[\ซ้าย| \begin(เมทริกซ์) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\end(เมทริกซ์) \right|\ ]
สารละลาย. เพื่อการเปลี่ยนแปลง คราวนี้เรามาทำงานกับคอลัมน์กัน ตัวอย่างเช่น คอลัมน์สุดท้ายมีศูนย์สองตัวพร้อมกัน ซึ่งแน่นอนว่าจะลดการคำนวณลงอย่างมาก ตอนนี้คุณจะเห็นว่าทำไม
ดังนั้นเราจึงขยายดีเทอร์มิแนนต์ในคอลัมน์ที่สี่:
\[\begin(align) \left| \begin(เมทริกซ์) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\end(เมทริกซ์) \right|= 0\cdot ((\left(-1 \right))^(1+4))\cdot \left| \begin(เมทริกซ์) 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\end(เมทริกซ์) \right|+ & \\ +1\cdot ((\left(-1 \ ขวา))^(2+4))\cdot \left| \begin(เมทริกซ์) 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\end(เมทริกซ์) \right|+ & \\ +1\cdot ((\left(-1 \ ขวา))^(3+4))\cdot \left| \begin(เมทริกซ์) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\end(เมทริกซ์) \right|+ & \\ +0\cdot ((\left(-1 \ ขวา))^(4+4))\cdot \left| \begin(เมทริกซ์) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end(เมทริกซ์) \right| & \\\end(จัดตำแหน่ง)\]
แล้ว - โอ้ ปาฏิหาริย์! - สองเทอมจะหมดไปทันที เนื่องจากมีตัวประกอบเป็น "0" ยังมีปัจจัยกำหนด 3x3 สองตัวเหลืออยู่ ซึ่งเราสามารถจัดการได้อย่างง่ายดาย:
\[\begin(align) & \left| \begin(เมทริกซ์) 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\end(เมทริกซ์) \right|=0+0+1-1-1-0=-1; \\ & \ซ้าย| \begin(เมทริกซ์) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\end(เมทริกซ์) \right|=0+1+1-0-0-1=1 \\\end(จัดแนว)\]
กลับไปที่แหล่งที่มาแล้วค้นหาคำตอบ:
\[\ซ้าย| \begin(เมทริกซ์) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\end(เมทริกซ์) \right|= 1\cdot \left(-1 \right)+\left(-1 \right)\cdot 1=-2\]
โอเค ตอนนี้ทุกอย่างจบลงแล้ว และข้อ 4! = ไม่ต้องนับ 24 เทอม :)
คำตอบ: −2
คุณสมบัติพื้นฐานของดีเทอร์มิแนนต์
ในปัญหาสุดท้าย เราเห็นว่าการมีศูนย์ในแถว (คอลัมน์) ของเมทริกซ์ช่วยลดความยุ่งยากในการสลายตัวของดีเทอร์มิแนนต์และโดยทั่วไปในการคำนวณทั้งหมดได้อย่างไร คำถามธรรมชาติเกิดขึ้น: เป็นไปได้หรือไม่ที่จะทำให้ศูนย์เหล่านี้ปรากฏแม้ในเมทริกซ์ซึ่งไม่ได้อยู่ที่นั่นตั้งแต่แรก?
คำตอบนั้นชัดเจน: สามารถ. และนี่คือคุณสมบัติของดีเทอร์มิแนนต์มาช่วยเรา:
- หากคุณสลับสองแถว (คอลัมน์) ดีเทอร์มิแนนต์จะไม่เปลี่ยนแปลง
- หากแถวหนึ่ง (คอลัมน์) คูณด้วยตัวเลข $k$ ตัวกำหนดทั้งหมดจะถูกคูณด้วยตัวเลข $k$ ด้วย
- หากคุณใช้บรรทัดหนึ่งแล้วบวก (ลบ) จากอีกบรรทัดหนึ่งกี่ครั้งก็ได้ตามที่คุณต้องการ ดีเทอร์มิแนนต์จะไม่เปลี่ยนแปลง
- หากดีเทอร์มิแนนต์สองแถวเท่ากันหรือเป็นสัดส่วน หรือแถวใดแถวหนึ่งเต็มไปด้วยศูนย์ ดีเทอร์มิแนนต์ทั้งหมดจะเท่ากับศูนย์
- คุณสมบัติข้างต้นทั้งหมดเป็นจริงสำหรับคอลัมน์เช่นกัน
- เมื่อย้ายเมทริกซ์ ดีเทอร์มิแนนต์จะไม่เปลี่ยนแปลง
- ดีเทอร์มิแนนต์ของผลคูณของเมทริกซ์ เท่ากับผลคูณของดีเทอร์มิแนนต์
คุณสมบัติประการที่สามมีคุณค่าเป็นพิเศษ: เราทำได้ ลบออกจากแถวหนึ่ง (คอลัมน์) อีกแถวหนึ่งจนกว่าศูนย์จะปรากฏในตำแหน่งที่ถูกต้อง.
โดยส่วนใหญ่ การคำนวณมักจะลงมาที่ "การทำให้คอลัมน์ทั้งหมดเป็นศูนย์" ยกเว้นองค์ประกอบเดียว จากนั้นจึงขยายดีเทอร์มิแนนต์ไปเหนือคอลัมน์นี้ เพื่อให้ได้เมทริกซ์ที่มีขนาดเล็กกว่า 1
มาดูกันว่าวิธีนี้ทำงานอย่างไรในทางปฏิบัติ:
งาน. ค้นหาปัจจัยกำหนด:
\[\ซ้าย| \begin(เมทริกซ์) 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\\end(เมทริกซ์) \right|\ ]
สารละลาย. ดูเหมือนจะไม่มีศูนย์เลยดังนั้นคุณสามารถ "เจาะ" ในแถวหรือคอลัมน์ใดก็ได้ - จำนวนการคำนวณจะใกล้เคียงกัน อย่าเสียเวลาไปกับเรื่องมโนสาเร่และ "ศูนย์ออก" ในคอลัมน์แรก: มันมีเซลล์ที่มีหนึ่งอยู่แล้วดังนั้นเพียงแค่ใช้บรรทัดแรกแล้วลบออก 4 ครั้งจากวินาที 3 ครั้งจากที่สามและ 2 ครั้งจากสุดท้าย
เป็นผลให้เราจะได้รับเมทริกซ์ใหม่ แต่ปัจจัยกำหนดจะเหมือนเดิม:
\[\begin(เมทริกซ์) \left| \begin(เมทริกซ์) 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\\end(เมทริกซ์) \right|\ เริ่มต้น(เมทริกซ์) \downarrow \\ -4 \\ -3 \\ -2 \\\end(เมทริกซ์)= \\ =\left| \begin(เมทริกซ์) 1 & 2 & 3 & 4 \\ 4-4\cdot 1 & 1-4\cdot 2 & 2-4\cdot 3 & 3-4\cdot 4 \\ 3-3\cdot 1 & 4-3\cdot 2 & 1-3\cdot 3 & 2-3\cdot 4 \\ 2-2\cdot 1 & 3-2\cdot 2 & 4-2\cdot 3 & 1-2\cdot 4 \ \\end(เมทริกซ์) \right|= \\ =\left| \begin(เมทริกซ์) 1 & 2 & 3 & 4 \\ 0 & -7 & -10 & -13 \\ 0 & -2 & -8 & -10 \\ 0 & -1 & -2 & -7 \\ \end(เมทริกซ์) \right| \\\end(เมทริกซ์)\]
ตอนนี้ ด้วยความใจเย็นของ Piglet เราจึงวางดีเทอร์มิแนนต์นี้ไว้ในคอลัมน์แรก:
\[\begin(เมทริกซ์) 1\cdot ((\left(-1 \right))^(1+1))\cdot \left| \begin(เมทริกซ์) -7 & -10 & -13 \\ -2 & -8 & -10 \\ -1 & -2 & -7 \\\end(เมทริกซ์) \right|+0\cdot ((\ ซ้าย(-1 \right))^(2+1))\cdot \left| ... \right|+ \\ +0\cdot ((\left(-1 \right))^(3+1))\cdot \left| ... \right|+0\cdot ((\left(-1 \right))^(4+1))\cdot \left| ... \ขวา| \\\end(เมทริกซ์)\]
เห็นได้ชัดว่าเฉพาะเทอมแรกเท่านั้นที่จะ "รอด" - ฉันไม่ได้เขียนปัจจัยที่เหลือด้วยซ้ำเนื่องจากพวกมันยังคงคูณด้วยศูนย์ ค่าสัมประสิทธิ์ที่อยู่ด้านหน้าดีเทอร์มิแนนต์เท่ากับ 1 นั่นคือ คุณไม่จำเป็นต้องเขียนมันลงไป
แต่คุณสามารถเอา "ข้อเสีย" ออกจากดีเทอร์มิแนนต์ทั้งสามบรรทัดได้ โดยพื้นฐานแล้ว เราได้เอาตัวประกอบ (−1) ออกมาสามครั้ง:
\[\ซ้าย| \begin(เมทริกซ์) -7 & -10 & -13 \\ -2 & -8 & -10 \\ -1 & -2 & -7 \\\end(เมทริกซ์) \right|=\cdot \left| \begin(เมทริกซ์) 7 & 10 & 13 \\ 2 & 8 & 10 \\ 1 & 2 & 7 \\\end(เมทริกซ์) \right|\]
เราได้รับดีเทอร์มิแนนต์ขนาดเล็ก 3x3 ซึ่งสามารถคำนวณได้แล้วโดยใช้กฎของสามเหลี่ยม แต่เราจะพยายามแยกย่อยออกเป็นคอลัมน์แรก - โชคดีที่บรรทัดสุดท้ายมีหนึ่งรายการอย่างภาคภูมิใจ:
\[\begin(align) & \left(-1 \right)\cdot \left| \begin(เมทริกซ์) 7 & 10 & 13 \\ 2 & 8 & 10 \\ 1 & 2 & 7 \\\end(เมทริกซ์) \right|\begin(เมทริกซ์) -7 \\ -2 \\ \uparrow \ \\end(เมทริกซ์)=\left(-1 \right)\cdot \left| \begin(เมทริกซ์) 0 & -4 & -36 \\ 0 & 4 & -4 \\ 1 & 2 & 7 \\\end(เมทริกซ์) \right|= \\ & =\cdot \left| \begin(เมทริกซ์) -4 & -36 \\ 4 & -4 \\\end(เมทริกซ์) \right|=\left(-1 \right)\cdot \left| \begin(เมทริกซ์) -4 & -36 \\ 4 & -4 \\\end(เมทริกซ์) \right| \\\end(จัดแนว)\]
แน่นอนว่าคุณยังคงสนุกและขยายเมทริกซ์ 2x2 ไปตามแถว (คอลัมน์) ได้ แต่คุณและฉันก็เพียงพอแล้ว ดังนั้นเราจะคำนวณคำตอบกัน:
\[\left(-1 \right)\cdot \left| \begin(เมทริกซ์) -4 & -36 \\ 4 & -4 \\\end(เมทริกซ์) \right|=\left(-1 \right)\cdot \left(16+144 \right)=-160\ ]
เท่านี้ความฝันก็สลายแล้ว คำตอบมีเพียง −160 เท่านั้น :)
คำตอบ: −160
หมายเหตุสองสามข้อก่อนที่เราจะไปยังงานสุดท้าย:
- เมทริกซ์ดั้งเดิมมีความสมมาตรเทียบกับเส้นทแยงมุมทุติยภูมิ ผู้เยาว์ทั้งหมดในส่วนขยายนั้นมีความสมมาตรด้วยความเคารพต่อเส้นทแยงมุมรองที่เหมือนกัน
- พูดอย่างเคร่งครัด เราไม่สามารถขยายสิ่งใดได้เลย แต่เพียงลดเมทริกซ์ให้อยู่ในรูปสามเหลี่ยมด้านบน เมื่อมีศูนย์ทึบอยู่ใต้เส้นทแยงมุมหลัก จากนั้น (ตามการตีความทางเรขาคณิตอย่างเคร่งครัด) ดีเทอร์มิแนนต์จะเท่ากับผลคูณของ $((a)_(ii))$ - ตัวเลขบนเส้นทแยงมุมหลัก
งาน. ค้นหาปัจจัยกำหนด:
\[\ซ้าย| \begin(เมทริกซ์) 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\\end(เมทริกซ์) \right|\ ]
สารละลาย. บรรทัดแรกตรงนี้ขอให้เป็น "ศูนย์" นำคอลัมน์แรกมาลบออกจากคอลัมน์อื่นๆ ทั้งหมดหนึ่งครั้ง:
\[\begin(align) & \left| \begin(เมทริกซ์) 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\\end(เมทริกซ์) \right|= \\ & =\ซ้าย| \begin(เมทริกซ์) 1 & 1-1 & 1-1 & 1-1 \\ 2 & 4-2 & 8-2 & 16-2 \\ 3 & 9-3 & 27-3 & 81-3 \\ 5 & 25-5 & 125-5 & 625-5 \\\end(เมทริกซ์) \right|= \\ & =\left| \begin(เมทริกซ์) 1 & 0 & 0 & 0 \\ 2 & 2 & 6 & 14 \\ 3 & 6 & 24 & 78 \\ 5 & 20 & 120 & 620 \\\end(เมทริกซ์) \right| \\\end(จัดแนว)\]
เราขยายไปตามแถวแรก จากนั้นนำปัจจัยทั่วไปออกจากแถวที่เหลือ:
\[\cdot \left| \begin(เมทริกซ์) 2 & 6 & 14 \\ 6 & 24 & 78 \\ 20 & 120 & 620 \\\end(เมทริกซ์) \right|=\cdot \left| \begin(เมทริกซ์) 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\\end(เมทริกซ์) \right|\]
เราเห็นตัวเลข "สวยงาม" อีกครั้ง แต่ในคอลัมน์แรก - เราจัดวางดีเทอร์มิแนนต์ตามนั้น:
\[\begin(align) & 240\cdot \left| \begin(เมทริกซ์) 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\\end(เมทริกซ์) \right|\begin(เมทริกซ์) \downarrow \\ -1 \\ -1 \ \\end(เมทริกซ์)=240\cdot \left| \begin(เมทริกซ์) 1 & 3 & 7 \\ 0 & 1 & 6 \\ 0 & 3 & 24 \\\end(เมทริกซ์) \right|= \\ & =240\cdot ((\left(-1 \ ขวา))^(1+1))\cdot \left| \begin(เมทริกซ์) 1 & 6 \\ 3 & 24 \\\end(เมทริกซ์) \right|= \\ & =240\cdot 1\cdot \left(24-18 \right)=1440 \\\end( จัดแนว)\]
คำสั่ง. ปัญหาได้รับการแก้ไขแล้ว
คำตอบ: 1440
สัมมนา 6
การคำนวณดีเทอร์มิแนนต์ของเมทริกซ์ คุณสมบัติของดีเทอร์มิแนนต์
ข้อมูลเบื้องต้น
ดีเทอร์มิแนนต์เมทริกซ์
แนวคิดของดีเทอร์มิแนนต์ของเมทริกซ์ ซึ่งเขียนแทนด้วย หรือ 
เหมาะสมสำหรับเมทริกซ์จตุรัสเท่านั้น ให้เราแนะนำแนวคิดนี้ตามลำดับ โดยเพิ่มมิติของเมทริกซ์
ตัวอย่าง. 
.
ตัวอย่าง.
ปัจจัยกำหนด n -ลำดับที่
คำนิยาม.องค์ประกอบรอง 
-เมทริกซ์ 
เรียกว่าปัจจัยกำหนด 
ลำดับที่สอดคล้องกับเมทริกซ์ที่ได้รับจากเมทริกซ์ 
หลังจากขีดฆ่าออกไปแล้ว 
-บรรทัดที่ และ 
คอลัมน์ที่ องค์ประกอบรอง
เราจะแสดงถึง 
.
ตัวอย่าง.อนุญาต
, แล้ว 
.
คำนิยาม.การบวกพีชคณิตขององค์ประกอบ 
งานนี้เรียกว่า 
ถึงผู้เยาว์ 
และถูกกำหนดไว้ 
, เช่น. 
.
ตัวอย่าง.อนุญาต
, แล้ว 
.
คำนิยาม.ปัจจัยกำหนด 
ลำดับที่ (หรือดีเทอร์มิแนนต์ของเมทริกซ์ 
) เรียกว่าตัวเลข 
, เท่ากัน 
. สูตร 
เรียกว่าการขยายตัวของดีเทอร์มิแนนต์ใน 
-บรรทัดที่
ตัวอย่าง.ลองขยายดีเทอร์มิแนนต์ดู
บนบรรทัดที่สองแล้วคำนวณ
.
สูตรสลายดีเทอร์มิแนนต์ของเมทริกซ์โดย 
- คอลัมน์ที่ 3 มีแบบฟอร์ม 
.
ตัวอย่าง.ลองขยายดีเทอร์มิแนนต์ดู
ตามคอลัมน์ที่สามแล้วคำนวณ
.
คุณสมบัติของดีเทอร์มิแนนต์.
ให้เราแสดงรายการคุณสมบัติหลักของปัจจัยกำหนด
ตัวอย่าง. 
.
8. หากองค์ประกอบทั้งหมดของแถว (คอลัมน์) ของดีเทอร์มิแนนต์มีค่าเท่ากับศูนย์ ดีเทอร์มิแนนต์เองก็จะเท่ากับศูนย์
9. หากองค์ประกอบของสองแถว (คอลัมน์) ของดีเทอร์มิแนนต์โดยคำนึงถึงลำดับของพวกมันนั้นเป็นสัดส่วนซึ่งกันและกัน ดีเทอร์มิแนนต์จะเท่ากับศูนย์
10. หากองค์ประกอบของแถวใดแถวหนึ่ง (คอลัมน์) ของดีเทอร์มิแนนต์เราเพิ่มองค์ประกอบที่สอดคล้องกันของอีกแถวหนึ่ง (คอลัมน์) คูณด้วยตัวเลขใดก็ได้ 
แล้วค่าของดีเทอร์มิแนนต์จะไม่เปลี่ยนแปลง
11. ดีเทอร์มิแนนต์ของเมทริกซ์สามเหลี่ยมเท่ากับผลคูณขององค์ประกอบบนเส้นทแยงมุมหลัก
การคำนวณดีเทอร์มิแนนต์โดยการขยายไปเหนือแถว (คอลัมน์) จะมีประสิทธิภาพเป็นพิเศษเมื่อแถวนี้ (คอลัมน์) มีองค์ประกอบเป็นศูนย์ ดังนั้นเมื่อคำนวณดีเทอร์มิแนนต์ขนาดใหญ่ ขอแนะนำให้สร้างแถว (คอลัมน์) ดังกล่าวโดยใช้คุณสมบัติที่ระบุไว้ของดีเทอร์มิแนนต์ก่อน
ตัวอย่าง. 
/
เพิ่มคอลัมน์ที่สามเข้ากับคอลัมน์ที่สอง/
/
ลบบรรทัดที่สี่ออกจากบรรทัดที่สาม/
/
ขยายดีเทอร์มิแนนต์ในคอลัมน์ที่สอง/ 
/ลบบรรทัดที่สองออกจากบรรทัดแรก/ 
/เพิ่มคอลัมน์ที่สามไปยังคอลัมน์ที่สอง/ 
/ขยายดีเทอร์มิแนนต์ในบรรทัดแรก/ 
/ คูณบรรทัดแรกด้วย 2 แล้วลบออกจากบรรทัดที่สอง / 
/ขยายดีเทอร์มิแนนต์ตามคอลัมน์แรก/
วิธีเกาส์.
ในวิธีเชิงตัวเลขจะใช้เมื่อคำนวณปัจจัยกำหนด วิธีเกาส์เซียน โดยพิจารณาจากการลดดีเทอร์มิแนนต์ให้อยู่ในรูปสามเหลี่ยมโดยใช้การแปลงข้างต้น
ตัวอย่าง.ให้เราคำนวณดีเทอร์มิแนนต์เดียวกันโดยใช้วิธีเกาส์เซียนเหมือนในตัวอย่างที่แล้ว
/
ลบแถวแรกจากแถวที่สองสามและสี่เราสร้างองค์ประกอบที่อยู่ในคอลัมน์แรกเป็นศูนย์ (ก่อนที่จะลบออกจากแถวที่สามให้คูณแถวแรกด้วย 3) /
/
สลับบรรทัดที่สามและสี่/
/
คูณบรรทัดที่สองด้วย
แล้วลบออกจากบรรทัดที่สี่/
/ ลบบรรทัดที่สามออกจากบรรทัดที่สี่ /
/โดยใช้คุณสมบัติของเมทริกซ์สามเหลี่ยม เราคำนวณดีเทอร์มิแนนต์/
วิธีความสัมพันธ์การเกิดซ้ำ.
ถ้าเมทริกซ์ที่เราคำนวณดีเทอร์มิแนนต์มีสมมาตรเพียงพอ เราก็สามารถใช้ได้ วิธีความสัมพันธ์การเกิดซ้ำ .
ตัวอย่าง.ให้เราคำนวณดีเทอร์มิแนนต์โดยใช้วิธีความสัมพันธ์ที่เกิดซ้ำ 
-ลำดับที่
.
มาแบ่งมันออกเป็นคอลัมน์สุดท้ายกัน
/
ตอนนี้เราขยายดีเทอร์มิแนนต์ในเทอมที่สองตามบรรทัดสุดท้าย /
.
เราสังเกตเห็นว่าตอนนี้เรามีปัจจัยกำหนดสามตัวที่มีโครงสร้างเดียวกัน แต่มีมิติต่างกัน ถ้าเราแทนดีเทอร์มิแนนต์ดั้งเดิม 
สั่งซื้อผ่าน 
จากนั้นเราก็สามารถเขียนความสัมพันธ์การเกิดซ้ำได้ 
. หากต้องการใช้ความสัมพันธ์นี้ เรามาคำนวณปัจจัยกำหนดแรกๆ กัน: 
.
สังเกตว่า 
. ดังนั้นเราจึงสามารถเขียนได้ เป็นต้น การคำนวณปัจจัยกำหนดแรกจะให้สูตรทั่วไป 
. เพื่อให้การพิสูจน์สมบูรณ์ เรามาตรวจสอบความถูกต้องของสูตรนี้โดยใช้การอุปนัยทางคณิตศาสตร์ สมมติว่าสูตรนี้ถูกต้องสำหรับดีเทอร์มิแนนต์ 
-ลำดับที่ เราต้องแสดงว่าดีเทอร์มิแนนต์ 
-ลำดับที่เท่ากับ 
. เราพบโดยใช้ความสัมพันธ์การเกิดซ้ำ ผลลัพธ์ที่ได้จะพิสูจน์ความถูกต้องของสูตร 
.
งาน
1. ปัญหาความซับซ้อนในระดับที่น่าพอใจ
คำนวณดีเทอร์มิแนนต์ลำดับที่สอง.
6.1.
.
6.2.
.
6.3.
.
6.4.
.
6.5.
.
6.6.
.
6.7.
.
6.8.
.
6.9.
.
6.10.
.
แก้สมการ
6.11.
.
6.12.
.
6.13.
.
6.14.
.
6.15.
.
6.16.
.
คำนวณปัจจัยกำหนด
6.17.
.
6.18.
.
6.19.
.
6.20.
.
6.21.
.
6.22.
.
6.23.
.
6.24.
.
6.25.
.
6.26.
.
คำนวณปัจจัยกำหนดโดยการขยายแถวหรือคอลัมน์บางคอลัมน์
6.27.
.
6.28.
.
6.29.
.
6.30.
.
6.31.
.
แก้สมการและอสมการ
6.32.
.
6.33.
.
6.34.
.
คำนวณปัจจัยกำหนด
6.35.
.
6.36.
.
6.37.
.
6.38.
.
6.39.
.
6.40.
.
2. งานที่มีระดับความซับซ้อนเพิ่มขึ้น
คำนวณปัจจัยกำหนด
6.41.
.
6.42.
.
6.43.
.
6.44.
.
คำนวณปัจจัยกำหนดโดยใช้วิธีความสัมพันธ์การเกิดซ้ำ
6.45.
.
6.46.
.
6.47.
.
6.48. โดยไม่ต้องคำนวณปัจจัยกำหนด ให้แสดงว่าหารด้วย:
ก) 
; ข) 
.
คำนวณโดยใช้คุณสมบัติของดีเทอร์มิแนนต์
6.49.
.
6.50.
.
การเสริมพีชคณิตและผู้เยาว์
ขอให้เรามีปัจจัยลำดับที่สาม: 
.
ส่วนน้อยสอดคล้องกับองค์ประกอบนี้ ไอจดีเทอร์มิแนนต์ลำดับที่สามเรียกว่าดีเทอร์มิแนนต์ลำดับที่สองที่ได้รับจากอันที่กำหนดโดยการลบแถวและคอลัมน์ที่จุดตัดขององค์ประกอบที่กำหนดนั่นคือ ฉัน-บรรทัดที่ และ เจคอลัมน์ที่ ผู้เยาว์ที่สอดคล้องกับองค์ประกอบที่กำหนด ไอจเราจะแสดงถึง เอ็มจ.
ตัวอย่างเช่น, ส่วนน้อย ม.12ซึ่งสอดคล้องกับองค์ประกอบ 12ก็จะมีปัจจัยกำหนด 
ซึ่งได้มาจากการลบแถวที่ 1 และคอลัมน์ที่ 2 ออกจากดีเทอร์มิแนนต์นี้
ดังนั้น สูตรที่กำหนดดีเทอร์มิแนนต์ลำดับที่สามแสดงให้เห็นว่าดีเทอร์มิแนนต์นี้เท่ากับผลรวมของผลิตภัณฑ์ขององค์ประกอบของแถวที่ 1 โดยผู้เยาว์ที่เกี่ยวข้อง ในกรณีนี้ผู้เยาว์ที่สอดคล้องกับองค์ประกอบ 12, ถูกนำโดยมีเครื่องหมาย “–” เช่น เราสามารถเขียนสิ่งนั้นได้
| . | (1) |
ในทำนองเดียวกัน เราสามารถแนะนำคำจำกัดความของผู้เยาว์สำหรับปัจจัยลำดับที่สองและปัจจัยลำดับที่สูงกว่าได้
ขอแนะนำอีกหนึ่งแนวคิด
ส่วนเสริมพีชคณิตองค์ประกอบ ไอจดีเทอร์มิแนนต์เรียกว่าผู้เยาว์ เอ็มจคูณด้วย (–1) i+j
ส่วนเสริมพีชคณิตขององค์ประกอบ ไอจแสดงโดย อาจ.
จากคำจำกัดความที่เราได้รับว่าการเชื่อมต่อระหว่างส่วนเสริมพีชคณิตขององค์ประกอบกับองค์ประกอบรองนั้นแสดงออกมาด้วยความเท่าเทียมกัน อาจ= (–1) ผม+เจ มิจ.
ตัวอย่างเช่น,
ตัวอย่าง.มีการกำหนดปัจจัยกำหนดไว้ หา เอ 13, เอ 21, เอ 32.
จะเห็นได้ง่ายว่าการใช้การบวกองค์ประกอบเชิงพีชคณิต สูตร (1) สามารถเขียนได้เป็น:
เช่นเดียวกับสูตรนี้ คุณสามารถขยายดีเทอร์มิแนนต์ให้เป็นองค์ประกอบของแถวหรือคอลัมน์ใดก็ได้
ตัวอย่างเช่น การสลายตัวของดีเทอร์มิแนนต์เป็นองค์ประกอบของแถวที่ 2 สามารถรับได้ดังนี้ ตามคุณสมบัติ 2 ของดีเทอร์มิแนนต์ เรามี:
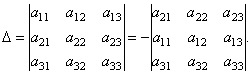
ให้เราขยายปัจจัยผลลัพธ์ให้เป็นองค์ประกอบของแถวที่ 1
 .
| (2) |
จากที่นี่ 
เพราะ ปัจจัยกำหนดลำดับที่สองในสูตร (2) เป็นตัวกำหนดรองขององค์ประกอบ 21 , 22 , 23. ดังนั้นนั่นคือ เราได้การสลายตัวของดีเทอร์มิแนนต์เป็นองค์ประกอบของแถวที่ 2
ในทำนองเดียวกัน เราสามารถหาส่วนขยายของดีเทอร์มิแนนต์ไปเป็นองค์ประกอบของแถวที่สามได้ การใช้คุณสมบัติ 1 ของดีเทอร์มิแนนต์ (เกี่ยวกับการขนย้าย) เราสามารถแสดงว่าส่วนขยายที่คล้ายกันนั้นใช้ได้เช่นกัน เมื่อขยายเหนือองค์ประกอบของคอลัมน์
ดังนั้นทฤษฎีบทต่อไปนี้จึงใช้ได้
ทฤษฎีบท (เกี่ยวกับการขยายตัวของดีเทอร์มิแนนต์เหนือแถวหรือคอลัมน์ที่กำหนด)ดีเทอร์มิแนนต์เท่ากับผลรวมของผลิตภัณฑ์ขององค์ประกอบของแถว (หรือคอลัมน์) ใด ๆ และการเสริมพีชคณิต
สิ่งที่กล่าวมาทั้งหมดเป็นจริงสำหรับปัจจัยกำหนดลำดับที่สูงกว่าด้วย
ตัวอย่าง.
เมทริกซ์ผกผัน
มีการแนะนำแนวคิดของเมทริกซ์ผกผันสำหรับเท่านั้น เมทริกซ์จตุรัส.
ถ้า กเป็นเมทริกซ์จตุรัสแล้ว ย้อนกลับเพราะเมทริกซ์ก็คือเมทริกซ์ซึ่งแสดงแทน เอ-1และเป็นไปตามเงื่อนไข (คำจำกัดความนี้ถูกนำมาใช้โดยการเปรียบเทียบกับการคูณตัวเลข)
