Impulsrespons fra filteret. Digitale filtre med endelig impulsrespons. Datautjevning. Medianfiltrering
48 Digitale filtre med endelig impulsrespons. Beregning av kih-filtre.
Finite Impulse Response Filter (Ikke-rekursivt filter, FIR filter) eller FIR-filter (FIR er forkortet fra finite impulse response - finite impulse response) - en av typene lineære digitale filtre, et karakteristisk trekk ved det er tidsbegrensningen impulsrespons(fra et tidspunkt blir det nøyaktig lik null). Et slikt filter kalles også ikke-rekursivt på grunn av manglende tilbakemelding. Nevneren for overføringsfunksjonen til et slikt filter er en viss konstant.
Differanseligning som beskriver forholdet mellom inngangs- og utgangssignalene til filteret: hvor P- filterrekkefølge, x(n) - inngangssignal, y(n) er utgangssignalet, og b Jeg- filterkoeffisienter. Med andre ord, verdien av en hvilken som helst utgangssignalprøve bestemmes av summen av de skalerte verdiene P tidligere avlesninger. Du kan si det annerledes: verdien av filterutgangen til enhver tid er verdien av responsen til den øyeblikkelige verdien av inngangen og summen av alle gradvis avtagende responser P tidligere signaleksempler som fortsatt påvirker utgangen (etter P-teller, blir pulsovergangsfunksjonen lik null, som allerede nevnt, derfor alle ledd etter P-th vil også bli lik null). La oss skrive den forrige ligningen i en mer romslig form:
For å finne filterkjernen legger vi
x(n) = δ( n)
hvor δ( n) - deltafunksjon. Da kan impulsresponsen til FIR-filteret skrives som:
Z-transformasjonen av impulsresponsen gir oss overføringsfunksjonen til FIR-filteret:
]Egenskaper
FIR-filteret har en rekke nyttige egenskaper som gjør det noen ganger å foretrekke å bruke enn et IIR-filter. Her er noen av dem:
FIR-filtre er robuste.
FIR-filtre krever ikke tilbakemelding når de implementeres.
Fasen til FIR-filtre kan gjøres lineær
Direkte form for FIR-filter
FIR-filtre kan implementeres ved hjelp av tre elementer: en multiplikator, en adderer og en forsinkelsesblokk. Alternativet vist i figuren er en direkte implementering av type 1 FIR-filtre.
Implementering av den direkte formen til FIR-filteret
Eksempel program
Nedenfor er et eksempel på FIR-filterprogram skrevet i C:
/* FIR-filter for 128 trykk */
float fir_filter(float input)
statisk flyte prøve;
acc = 0,0f; /* Batteri */
/* Multipliser og akkumuler */
for (i = 0; i< 128; i++) {
acc += (h[i] * prøve[i]);
/* Exit */
/* Skift det forsinkede signalet */
for (i = 127; i > 0; i--)
sample[i] = sample;
49 Datautjevning. Glidende gjennomsnitt.
50 Datautjevning. Parabolsk utjevning.
51 Datautjevning. Spencer utjevning.
52 Datautjevning. Medianfiltrering.
Glidende gjennomsnitt, parabolsk utjevning, Spencer-utjevning, medianfiltrering
Når man utvikler metoder for å bestemme parametrene til fysiske prosesser som sakte endres over tid, er en viktig oppgave å eliminere påvirkningen av støyeffekter eller tilfeldig interferens som er lagt på det behandlede signalet som mottas ved utgangen til den primære omformeren.
For å eliminere denne effekten kan du bruke datautjevning. En av de enkleste metodene for slik utjevning er aritmetisk gjennomsnittsberegning. Når du bruker den, beregnes hver verdi av en diskret funksjon (behandlet datamatrise) i samsvar med uttrykket:
hvor er antall poeng for aritmetisk gjennomsnittsberegning (oddetall);
Verdien av funksjonen før behandling;
Det er andre ganske effektive metoder for utjevning, for eksempel med paraboler av andre grad på fem, syv, ni og elleve punkter i samsvar med uttrykkene:
eller parabler av fjerde grad på syv, ni, elleve og tretten poeng:
I praktiske applikasjoner gir andre effektive metoder, for eksempel 15-punkts Spencer-utjevning, gode resultater:
Ved å erstatte den komplekse eksponentielle , hvor inn i disse uttrykkene, kan vi bestemme overføringsfunksjonen til den tilsvarende transformasjonen.
For aritmetisk gjennomsnittsberegning
Uttrykket i parentes representerer en geometrisk progresjon med en nevner, derfor kan dette uttrykket representeres som:
.
Denne formelen representerer overføringskarakteristikken til et lavpassfilter, og den viser at jo flere termer som er involvert i gjennomsnitt, desto større undertrykkelse av høyfrekvente støykomponenter i signalet (se figur 6.1).
Imidlertid skiller det semantiske konseptet av frekvens ved behandling av tidstrender seg fra et lignende konsept ved behandling av signaler. Dette forklares med det faktum at når man studerer tidstrender, er det ikke deres frekvenssammensetning som er av interesse, men typen endring (økning, reduksjon, konstans, syklisitet, etc.).
Bruken av såkalte heuristiske algoritmer er også ganske effektiv for å jevne ut data.
En av dem er medianfiltrering. Under implementeringen i et glidende tidsvindu av dimensjon , der heltallet er et oddetall, erstattes det sentrale elementet av det midterste elementet i sekvensen, som er ordnet, i stigende rekkefølge av verdier, elementer i datamatrisen til den glattede signal som faller innenfor tidsvinduet. Fordelen med medianfiltrering er muligheten til å fjerne impulsstøy, hvis varighet ikke overskrider, med praktisk talt ingen forvrengning av jevnt varierende signaler. Denne metoden for støydemping har ikke en streng matematisk begrunnelse, men enkelheten til beregninger og effektiviteten til resultatene har ført til utbredt bruk.
Figur 6.1 - Overføringskarakteristiske grafer
aritmetiske gjennomsnittsoperasjoner for m=5, 7, 9, 11
En annen interessant utjevningsalgoritme er mediangjennomsnitt. Dens essens er som følger. I et glidende tidsvindu av størrelse (-odd heltall), er elementene i datamatrisen ordnet i stigende rekkefølge, og deretter fjernes de første og siste elementene fra den ordnede sekvensen (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
Denne metoden lar deg undertrykke puls- og radiofrekvensinterferens, samt oppnå god signalutjevning.
| " |
La oss vurdere det enkleste av digitale filtre - filtre med konstante parametere.
Inngangssignalet til det digitale filteret leveres i form av en sekvens av numeriske verdier som følger med intervaller (fig. 4.1, a). Når hver neste signalverdi mottas i det digitale filteret, beregnes neste verdi av utgangssignalet.Beregningsalgoritmer kan være svært forskjellige; under beregningsprosessen, i tillegg til den siste verdien av inngangssignalet, kan brukes
tidligere verdier for inngangs- og utgangssignalene: Utgangssignalet til et digitalt filter er også en sekvens av numeriske verdier som følger et intervall på . Dette intervallet er det samme for hele den digitale signalbehandlingsenheten.
Ris. 4.1. Signal ved inngang og utgang til digitalfilteret
Derfor, hvis du bruker det enkleste signalet i form av en enkelt puls til inngangen til et digitalt filter (fig. 4.2, a)
så ved utgangen får vi et signal i form av en diskret sekvens av numeriske verdier, som følger med intervaller
I analogi med konvensjonelle analoge kretser vil vi kalle dette responssignalet for impulsresponsen til filteret (fig. 4.2, b). I motsetning til impulsresponsen til en analog krets, er funksjonen dimensjonsløs.
Ris. 4.2. Enhetsimpuls og impulsrespons for et digitalt filter
La oss bruke et vilkårlig diskret signal til filterinngangen (fig. 4.1, a), som er et sett med diskrete verdier
Under handlingen til det første elementet dannes en sekvens multiplisert med ved utgangen av filteret; under handlingen multipliseres en sekvens med og forskyves til høyre med et beløp, osv. Som et resultat vil utgangen oppnå rekkefølge hvor
Dermed er utgangssignalet definert som den diskrete konvolusjonen av inngangssignalet og impulsresponsen. I denne forbindelse ligner digitale filtre på konvensjonelle kretser, der utgangssignalet er lik konvolusjonen av inngangssignalet og impulsresponsen.
Formel (4.1) er en digital filtreringsalgoritme. Hvis impulsresponsen til et filter er beskrevet av en sekvens med et begrenset antall ledd, kan filteret implementeres i form av en krets vist i fig. 4.3. Her indikerer bokstaven elementene for signalforsinkelse for tid (per celle); -elementer som multipliserer signalet med den tilsvarende koeffisienten.
Diagrammet vist i fig. 4.3 er ikke en elektrisk krets til et digitalt filter; Dette diagrammet er en grafisk representasjon av den digitale filtreringsalgoritmen og viser sekvensen av aritmetiske operasjoner utført under signalbehandling.
Ris. 4.3. Ikke-rekursiv digital filterkrets
For digitale filtre som behandler signaler i form av abstrakte numeriske sekvenser, er ikke konseptet "tidsforsinkelse" helt riktig. Derfor er elementer som forsinker signalet med én celle vanligvis merket på digitale filterkretser med et symbol som indikerer signalforsinkelsen på språket -transformasjoner. I det følgende vil vi holde oss til denne notasjonen.
La oss gå tilbake til den digitale filterkretsen vist i fig. 4.3, Slike filtre, der bare verdiene til inngangssignalet brukes til beregning, kalles enkle eller ikke-rekursive.
Den ikke-rekursive filteralgoritmen er lett å skrive hvis impulsresponsen til filteret er kjent. For den praktiske implementeringen av algoritmen er det nødvendig at impulsresponsen inneholder et begrenset antall ledd. Hvis impulsresponsen inneholder et uendelig antall termer, men de raskt synker i verdi, kan du begrense deg til et begrenset antall termer, og forkaste de som har små verdier. Hvis elementene i impulsresponsen ikke synker i verdi, viser den ikke-rekursive filteralgoritmen seg å være urealiserbar.
Ris. 4.4. -kjede
Som et eksempel kan du vurdere det enkleste digitale filteret, lik -kretsen (fig. 4.4). Impulsresponsen til kretsen har formen
For å skrive impulsresponsen til det tilsvarende digitale filteret, bør uttrykket erstattes av Impulsresponsen til en krets har imidlertid en dimensjon, og impulsresponsen til et digitalt filter må være dimensjonsløs. Derfor utelater vi multiplikatoren i uttrykk (4.2) og skriver impulsresponsen til det digitale filteret på skjemaet
En slik impulsrespons inneholder uendelig mange termer, men deres størrelse avtar i henhold til en eksponentiell lov, og vi kan begrense oss til termer ved å velge slik at
Nå kan vi skrive uttrykket for signalet ved filterutgangen
Dette uttrykket er også en digital filteralgoritme. Diagrammet av dette filteret er vist i fig. 4.5.
Den andre tilnærmingen til å analysere prosesser i digitale filtre ligner på operatørmetoden for å analysere konvensjonelle analoge kretser, bare i stedet for Laplace-transformasjonen, brukes -transformen.
Ris. 4.5. Krets til et ikke-rekursivt digitalt filter som ligner på en -krets
La oss definere en digital filterparameter som ligner på overføringsfunksjonen til en elektrisk krets. For å gjøre dette, bruk en transformasjon til impulsresponsen til et digitalt filter:
Funksjonen kalles systemfilterfunksjonen.
I samsvar med uttrykk (4.1) er signalet ved utgangen til det digitale filteret lik den diskrete konvolusjonen av inngangssignalet og impulsresponsen til filteret. Ved å bruke konvolusjonsteoremet på dette uttrykket får vi at utgangssignaltransformasjonen er lik inngangssignaltransformasjonen multiplisert med systemfilterfunksjonen:
Dermed spiller systemfunksjonen rollen som overføringsfunksjonen til et digitalt filter.
Som et eksempel, la oss finne systemfunksjonen til et førsteordens digitalt filter som ligner på en -krets:
Den tredje metoden for å analysere passasjen av signaler gjennom digitale filtre ligner den klassiske metoden for differensialligninger. La oss vurdere denne metoden ved å bruke ordrekjeder som et eksempel.
Den enkleste analoge kretsen av 1. orden er -kretsen (se fig. 4.4), passasjen av signaler som er beskrevet av differensialligningen
For en diskret krets, i stedet for differensialligningen (4.8), bør en differanseligning skrives, der inngangs- og utgangssignalene er spesifisert for diskrete tidspunkter, og i stedet for den deriverte, bør forskjellen mellom tilstøtende signalverdier vises. For en diskret 1. ordens krets kan differanseligningen skrives i en ganske generell form
La oss bruke transformasjonen på ligningen
hvor vi finner systemfilterfunksjonen
Formel (4.10) er et ganske generelt uttrykk for systemfunksjonen til et 1. ordens digitalt filter. Når det faller sammen med det tidligere oppnådde uttrykket (4.7) for systemfunksjonen til et digitalt filter som tilsvarer en -krets.
La oss finne en digital filtreringsalgoritme som tilsvarer systemfunksjonen (4.10). For å gjøre dette løser vi ligning (4.9) for
Et ekvivalent diagram av denne algoritmen er vist i fig. 4.6. Sammenlignet med et ikke-rekursivt filter (se fig. 4.5) er det lagt til en slags "feedback-krets" her, som betyr at verdiene til utgangssignalet brukes i påfølgende
Ris. 4.6. Krets til et rekursivt digitalt filter som ligner på en -krets
beregninger. Filtre av denne typen kalles rekursive.
Algoritme (4.11) tilsvarer et filter som er fullstendig ekvivalent med det ikke-rekursive filteret vurdert tidligere. Men for å bestemme én verdi av utgangssignalet ved hjelp av den ikke-rekursive filteralgoritmen (4.4), er det nødvendig å utføre operasjoner, og når du bruker den rekursive filteralgoritmen (4.11), kreves det bare to operasjoner. Dette er hovedfordelen med rekursive filtre. I tillegg tillater rekursive filtre signalbehandling med høyere nøyaktighet, siden de tillater en mer korrekt implementering av impulsresponsen uten å forkaste "halen". Rekursive filtre lar deg implementere algoritmer som ikke kan implementeres i det hele tatt ved bruk av ikke-rekursive filtre. For eksempel, med et filter som fungerer i henhold til kretsen i fig. 4.6, er i hovedsak en ideell akkumulator-integrator og har en impulsrespons av formen Et filter med en slik karakteristikk kan ikke implementeres ved bruk av et ikke-rekursivt skjema.
De vurderte eksemplene viser at det ikke er noen vits i å bruke ikke-rekursive algoritmer for å lage digitale filtre med lang impulsrespons. I disse tilfellene er det mer hensiktsmessig å bruke rekursive filtre.
Anvendelsesområdet for ikke-rekursive algoritmer er implementeringen av digitale filtre med en impulsrespons som inneholder et lite antall termer. Et eksempel er den enkleste differensiatoren, hvis utgangssignal er lik økningen av inngangssignalet:
Kretsen til et slikt digitalt filter er vist i fig. 4.7.
Ris. 4.7. Krets av den enkleste digitale differensiatoren
La oss nå vurdere et generelt digitalt filter, som er beskrevet av ligningen
Denne ligningen kan betraktes både som en differanseligning av orden og som en digital filtreringsalgoritme, hvis den skrives om annerledes, nemlig
Ris. 4.8. Rekursiv digital ordensfilterkrets
Algoritmen (4.13) tilsvarer kretsen vist i fig. 4.8. La oss finne systemfunksjonen til et slikt filter. For å gjøre dette, bruk transformasjonen på ligningen:
Uttrykk (4.14) lar oss etablere en sammenheng mellom fluktuasjonene til elementene i filterkretsen og systemfunksjonen. Koeffisientene i telleren til systemfunksjonen bestemmer verdiene til koeffisientene for
(i den ikke-rekursive delen av filteret), og koeffisientene i nevneren bestemmer den rekursive delen av filteret.
Det hele startet da en venn av en venn av en venn trengte hjelp med de samme filtrene. Gjennom Jedi-måtene nådde rykter om dette meg, jeg meldte meg av i kommentarene til innlegget ved lenken. Det så ut til å hjelpe. Vel, håper jeg.
Denne historien vekket minner fra den tredje, eller noe sånt, da jeg selv tok DSP, og fikk meg til å skrive en artikkel for alle de som er interessert i hvordan digitale filtre fungerer, men som naturlig nok er skremt av over -the-top formler og psykedeliske tegninger i (jeg allerede jeg snakker ikke om lærebøker).
Generelt, etter min erfaring, er situasjonen med lærebøker beskrevet av den velkjente setningen at noen ganger kan du ikke se skogen for trærne. Og det vil si at når de umiddelbart begynner å skremme deg med Z-transformen og formler for å dele polynomer, som ofte er lengre enn to brett, tørker interessen for temaet ekstremt raskt opp. Vi starter med en enkel en; heldigvis, for å forstå hva som skjer, er det slett ikke nødvendig å beskrive lange komplekse uttrykk.
Så, først, noen enkle grunnleggende konsepter.
1. Impulsrespons.
La oss si at vi har en boks med fire pinner. Vi aner ikke hva som er inni, men vi vet med sikkerhet at de to venstre terminalene er inngangen, og de to høyre er utgangen. La oss prøve å bruke en veldig kort puls med veldig stor amplitude på den og se hva som skjer ved utgangen. Vel, det er ikke klart hva som er inne i denne firpolen, fordi det ikke er klart hvordan den skal beskrives, men i det minste vil vi se noe.
Her må det sies at en kort (generelt sett, uendelig kort) puls med stor (generelt sett, uendelig) amplitude i teorien kalles en deltafunksjon. Forresten, det morsomme er at integreringen av dette endeløs funksjon er lik en. Dette er normaliseringen.
Så det vi så ved utgangen av firpolnettverket, etter å ha brukt deltafunksjonen på inngangen, kalles impulsrespons denne firpolen. Foreløpig er det imidlertid ikke klart hvordan det vil hjelpe oss, men la oss bare huske resultatet og gå videre til neste interessante konsept.
2. Konvolusjon.
Kort sagt, konvolusjon er en matematisk operasjon som handler om å integrere produktet av funksjoner:
Som du kan se, er det indikert med en stjerne. Du kan også se at under konvolusjon tas den ene funksjonen i sin "fremover" rekkefølge, og vi går gjennom den andre "back to front". Selvfølgelig, i det diskrete tilfellet, som er mer verdifullt for menneskeheten, går konvolusjon, som enhver integral, inn i summering:
Det vil virke som en slags kjedelig matematisk abstraksjon. Men faktisk er en bunt kanskje det mest magiske fenomenet i denne verden, nest bare i utrolighet etter fødselen av en person, med den eneste forskjellen er at de fleste finner ut hvor barn kommer fra i det minste i en alder av atten, mens om hva en konvolusjon er og hvorfor den er nyttig og fantastisk, har en stor del av jordens befolkning absolutt ingen anelse hele livet.
Så kraften til denne operasjonen ligger i det faktum at hvis f er et hvilket som helst vilkårlig inngangssignal, og g er impulsresponsen til et fire-ports nettverk, så vil resultatet av konvolusjonen av disse to funksjonene være lik det vi ville få ved å sende signalet f gjennom dette fire-ports nettverket.
Det vil si at impulsresponsen er en fullstendig cast av alle egenskapene til fireportsnettverket i forhold til inngangseffekten, og konvolusjon av inngangssignalet med det lar deg gjenopprette det tilsvarende utgangssignalet. Etter min mening er dette rett og slett fantastisk!
3. Filtre.
Du kan gjøre mange interessante ting med impulsrespons og konvolusjon. For eksempel, hvis signalet er lyd, kan du organisere romklang, ekko, refreng, flanger og mye, mye mer; du kan differensiere og integrere... Generelt kan du lage hva som helst. For oss nå er det viktigste at filtre selvfølgelig også enkelt kan fås ved hjelp av konvolusjon.
Det digitale filteret i seg selv er konvolusjonen av inngangssignalet med en impulsrespons som tilsvarer det ønskede filteret.
Men selvfølgelig må impulsresponsen oppnås på en eller annen måte. Vi har selvfølgelig allerede funnet ut hvordan vi skal måle det ovenfor, men i en slik oppgave er det liten mening i dette - hvis vi allerede har satt sammen filteret, hvorfor måle noe annet, kan vi bruke det som det er. Og dessuten er den viktigste verdien av digitale filtre at de kan ha egenskaper som er uoppnåelige (eller svært vanskelige å oppnå) i virkeligheten - for eksempel lineær fase. Så det er ingen måte å måle her i det hele tatt, du må bare telle.
4. Oppnå impulsrespons.
På dette tidspunktet, i de fleste publikasjoner om emnet, begynner forfatterne å dumpe fjell av Z-transformasjoner og fraksjoner fra polynomer på leseren, og forvirrer ham fullstendig. Jeg vil ikke gjøre dette, jeg vil bare kort forklare hva alt dette handler om og hvorfor det i praksis ikke er veldig nødvendig for den progressive offentligheten.
La oss si at vi har bestemt oss for hva vi vil ha fra et filter og laget en ligning som beskriver det. Deretter, for å finne impulsresponsen, kan du erstatte deltafunksjonen i den avledede ligningen og få den ønskede. Det eneste problemet er hvordan du gjør dette, fordi deltafunksjonen er i tide O regionen er gitt av et utspekulert system, og generelt er det alle slags uendeligheter. Så på dette stadiet viser alt seg å være fryktelig vanskelig.
Det er her det hender de husker at det er noe slikt som Laplace-transformasjonen. I seg selv er det ikke et halvt kilo rosiner. Den eneste grunnen til at det tolereres i radioteknikk er nettopp det faktum at i rommet av argumentet som denne transformasjonen er en overgang til, blir noen ting faktisk enklere. Spesielt den samme deltafunksjonen som ga oss så mye trøbbel i tidsdomenet er veldig lett å uttrykke - der er det bare en!
Z-transformen (aka Laurent-transformasjonen) er en versjon av Laplace-transformasjonen for diskrete systemer.
Det vil si at ved å bruke Laplace-transformasjonen (eller Z-transformasjonen, etter behov) på funksjonen som beskriver det ønskede filteret, erstatte en til den resulterende og transformere tilbake, får vi impulsresponsen. Det høres enkelt ut, alle kan prøve det. Jeg vil ikke risikere det, for som allerede nevnt er Laplace-transformasjonen en tøff ting, spesielt den omvendte. La oss la det være en siste utvei, og vi vil se etter noen enklere måter å få det vi leter etter. Det er flere av dem.
For det første kan vi huske et annet fantastisk faktum i naturen - amplitude-frekvens- og impulskarakteristikkene er relatert til hverandre av den gode og velkjente Fourier-transformasjonen. Dette betyr at vi kan tegne hvilken som helst frekvensrespons etter vår smak, ta den inverse Fourier-transformasjonen fra den (enten kontinuerlig eller diskret) og få impulsresponsen til systemet som implementerer den. Dette er rett og slett fantastisk!
Dette vil imidlertid ikke være problemfritt. For det første vil impulsresponsen vi får mest sannsynlig være uendelig (jeg vil ikke gå inn på forklaringer på hvorfor; det er slik verden fungerer), så vi må ta en frivillig beslutning om å kutte den av på et tidspunkt (innstilling). den er lik null utover det punktet). Men dette vil ikke skje bare slik - konsekvensen av dette, som man kunne forvente, vil være forvrengning av frekvensresponsen til det beregnede filteret - det vil bli bølget, og frekvensavskjæringen vil bli uskarp.
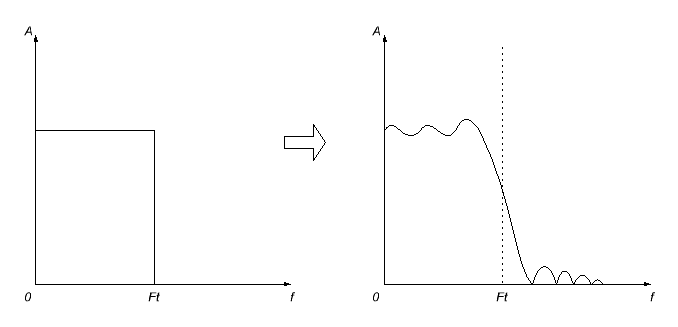
For å minimere disse effektene, brukes forskjellige utjevningsvindusfunksjoner på den forkortede impulsresponsen. Som et resultat blir frekvensresponsen vanligvis enda mer uskarp, men ubehagelige (spesielt i passbåndet) svingninger forsvinner. 
Faktisk, etter en slik prosessering får vi en arbeidsimpulsrespons og kan bygge et digitalt filter.
Den andre beregningsmetoden er enda enklere - impulsresponsene til de mest populære filtrene har lenge vært uttrykt i analytisk form for oss. Alt som gjenstår er å erstatte verdiene dine og bruke vindusfunksjonen på resultatet etter din smak. Så du trenger ikke engang vurdere noen transformasjoner.
Og, selvfølgelig, hvis målet er å etterligne oppførselen til en spesifikk krets, kan du få impulsresponsen i simulatoren:
Her påførte jeg en puls på 100500 volt (ja, 100,5 kV) med en varighet på 1 μs til inngangen til RC-kretsen og fikk dens impulsrespons. Det er klart at dette ikke lar seg gjøre i virkeligheten, men i simulatoren fungerer denne metoden, som du kan se, utmerket.
5. Merknader.
Det som ble sagt ovenfor om å forkorte impulsresponsen gjaldt selvsagt den såkalte. endelige impulsresponsfiltre (FIR/FIR-filtre). De har en haug med verdifulle egenskaper, inkludert lineær fase (under visse forhold for å konstruere impulsresponsen), som sikrer fravær av signalforvrengning under filtrering, samt absolutt stabilitet. Det finnes også uendelige impulsresponsfiltre (IIR/IIR-filtre). De er mindre ressurskrevende når det gjelder beregninger, men har ikke lenger de oppførte fordelene.
I den neste artikkelen håper jeg å se på et enkelt eksempel på praktisk implementering av et digitalt filter.
NOVOSIBIRSK STATTS TEKNISKE UNIVERSITET
FAKULTET FOR AUTOMATISERING OG DATATEKNIKK
Institutt for datainnsamlings- og behandlingssystemer
Disiplin "Teori og signalbehandling"
LABORATORIEARBEID NR.10
DIGITALE FILTRE
MED ENDELIG IMPULS KARAKTERISTIKK
Gruppe: AT-33
Alternativ: 1 Lærer:
Student: Shadrina A.V. Assoc. Shchetinin Yu.I.
Målet med arbeidet: studie av metoder for analyse og syntese av endelige impulsresponsfiltre ved bruk av utjevningsvindusfunksjoner.
Fullføring av arbeidet:
1. Impulsresponsplott av et lavpass FIR-filter med en rektangulær vindusgrensefrekvens for verdier av filterlengde og .
Impulsresponsen til et ideelt diskret FIR-filter har uendelig lengde og er ikke null for negative verdier på:
.
For å oppnå et fysisk gjennomførbart filter, bør man begrense impulsresponsen til et endelig tall, og deretter flytte den avkortede responsen til høyre med et beløp.
Verdien er lengden (størrelsen) på filteret, 
– filterrekkefølge.
Matlab-skript (labrab101.m)
N = input("Skriv inn filterlengde N = ");
h = sin(wc.*(n-(N-1)/2))./(pi.*(n-(N-1)/2));
xlabel("Referansenummer, n")
>> delplott(2,1,1)
>> labrab101
Angi filterlengde N = 15
>> tittel("Impulsrespons av FIR-filter for N=15")
>> delplott(2,1,2)
>> labrab101
Angi filterlengde N = 50
>> tittel("Impulsrespons av FIR-filter for N=50")
Figur 1. Impulsresponsplott av et lavpass FIR-filter med en rektangulær vindusgrensefrekvens for verdier av filterlengde og
En kommentar: Hvis vi ser på frekvensresponsen til et digitalt filter som en Fourier-serie: 
, da vil koeffisientene til denne serien representere verdiene til impulsresponsen til filteret. I dette tilfellet ble Fourier-serien trunkert i det første tilfellet til , og i det andre - til , og deretter ble de avkortede karakteristikkene forskjøvet langs prøveaksen til høyre for å få et årsaksfilter. Når bredden på hovedloben er 2, og når - 1, dvs. Når filterlengden øker, smalner hovedloben til impulsresponsen inn. Hvis vi vurderer nivået på sidelappene (ved å bruke ), så øker det i absolutt verdi med økende fra til . Dermed kan vi konkludere med at når du bruker en tilnærming av den ideelle frekvensresponsen til et filter med et rektangulært vindu, er det umulig å samtidig begrense hovedloben (og dermed redusere overgangsregionen) og redusere nivåene til sidelobene (redusere krusning i passbåndet og stoppbåndet til filteret). Den eneste kontrollerbare parameteren til et rektangulært vindu er størrelsen, som du kan påvirke bredden på hovedloben med, men det har ikke mye effekt på sidelobene.
2. Beregning av DVFT for impulskarakteristikkene fra trinn 1 ved hjelp av funksjonen. Grafer over deres frekvensrespons på en lineær skala og i desibel for 512 frekvensprøver. Passbånd, overgangsbånd og stoppbånd for filteret. Påvirkningen av filterrekkefølgen på bredden av overgangsbåndet og nivået av frekvensresponsrippel i pass- og stoppbåndene.
Matlab-funksjon (DTFT.m)
funksjon = DTFT(x,M)
N = maks(M, lengde(x));
% Reduserer FFT til størrelse 2^m
N = 2^(tak(log(N)/log(2)));
% Beregn fft
% Frekvensvektor
w = 2*pi*((0:(N-1))/N);
w = w - 2*pi*(w>=pi);
% Skift FFT for å gå fra -pi til +pi
X = fftshift(X);
w = fftshift(w);
Matlab Script (labrab102.m)
h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));
h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));
DTFT(h1,512);
DTFT(h2,512);
plot(w./(2*pi),abs(H1)./max(abs(H1)),,"r")
xlabel("f, Hz"), ylabel("|H1|/max(|H1|)"), rutenett
plot(w./(2*pi),abs(H2)./max(abs(H2)),,"b")
xlabel("f, Hz"), ylabel("|H2|/max(|H2|)"), rutenett
plot(w./(2*pi),20*log10(abs(H1)),,"r")
title("Frekvensrespons for et lavpass FIR-filter med et rektangulært vindu for N = 15")
xlabel("f, Hz"), ylabel("20lg(|H1|), dB"), rutenett
plot(w./(2*pi),20*log10(abs(H2)),"b")
title("Frekvensrespons for et lavpass FIR-filter med et rektangulært vindu for N = 50")
xlabel("f, Hz"), ylabel("20lg(|H2|), dB"), rutenett
Fig.2. Frekvensresponsplott av et lavpass FIR-filter med en rektangulær vindusgrensefrekvens for filterlengdeverdier og på en lineær skala
Fig.3. Frekvensresponsplott av et lavpass FIR-filter med en rektangulær vindusgrensefrekvens for filterlengdeverdier og på en logaritmisk skala
En kommentar:
Tabell 1. Rekkevidde for passbånd, overgangsområde og stoppbånd for filterlengde og
|
Filterlengde |
Båndbredde, Hz |
Overgangsregion, Hz |
Stoppbånd, Hz |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Forelesning nr. 10 "Digitale filtre med endelig impulsrespons" Overføringsfunksjonen til et fysisk realiserbart digitalt endelig impulsresponsfilter (FIR-filter) kan representeres som (10.1). Ved erstatning i uttrykk (10.1) får vi frekvensresponsen til FIR-filteret i formen Hvor Faseforsinkelse filter er definert som Gruppeforsinkelse filter er definert som Et særtrekk ved FIR-filtre er muligheten til å implementere konstante fase- og gruppeforsinkelser, dvs. lineær faserespons (10.5), hvor en - konstant. Hvis denne betingelsen er oppfylt, vil ikke signalet som passerer gjennom filteret forvrenger formen. For å utlede betingelsene som sikrer en lineær faserespons, skriver vi frekvensresponsen til FIR-filteret under hensyntagen til (10.5) Ved å sette likhetstegn mellom de virkelige og imaginære delene av denne likheten får vi Dividere den andre ligningen med den første, får vi Endelig kan vi skrive Denne ligningen har to løsninger. Først når en =0 tilsvarer ligningen Denne ligningen har en unik løsning som tilsvarer en vilkårlig h (0) (sin (0)=0), og h (n)=0 for n >0. Denne løsningen tilsvarer et filter hvis impulsrespons har en enkelt prøve som ikke er null ved det første tidspunktet. Et slikt filter er ikke av praktisk interesse. Vi finner en annen løsning for . I dette tilfellet får vi kryssmultiplikering av tellerne og nevnerne i (10.8) (10.11). Herfra har vi Siden denne ligningen har form av en Fourier-serie, er løsningen, hvis den eksisterer, unik. Det er lett å se at løsningen på denne ligningen må tilfredsstille betingelsene (10.13), (10.14). Fra betingelse (10.13) følger det at for hver filterordre N det er bare én faseforsinkelse en , hvor streng linearitet av faseresponsen kan oppnås. Av betingelse (10.14) følger det at impulsresponsen til filteret må være symmetrisk om punktet for oddetall N , og i forhold til midtpunktet av intervallet (fig. 10.1).
Frekvensresponsen til et slikt filter (for odd N ) kan skrives i skjemaet (10.15). Foreta en erstatning i det andre beløpet m = N -1- n , får vi (10.16). Siden h (n)= h (N -1- n ), så kan de to summene kombineres Bytter, får vi (10.18). Hvis vi utpeker så kan vi endelig skrive For et filter med en lineær faserespons har vi altså For tilfelle av selv N tilsvarende vil vi ha Å gjøre et bytte i den andre summen, får vi Å gjøre byttet, får vi (10.24). Etter å ha utpekt vi skal endelig ha Altså for et FIR-filter med lineær faserespons og jevn rekkefølge N kan skrives I det følgende vil vi for enkelhets skyld kun vurdere filtre med en merkelig rekkefølge. Ved syntetisering av filteroverføringsfunksjonen er de første parametrene som regel kravene til frekvensresponsen. Det er mange teknikker for å syntetisere FIR-filtre. La oss se på noen av dem. Siden frekvensresponsen til ethvert digitalt filter er en periodisk funksjon av frekvens, kan den representeres som en Fourier-serie hvor koeffisientene til Fourier-serien er like Det kan sees at koeffisientene til Fourier-serien h(n ) faller sammen med impulsrespons-koeffisientene til filteret. Derfor, hvis den analytiske beskrivelsen av den nødvendige frekvensresponsen til filteret er kjent, er det mulig å enkelt bestemme koeffisientene til impulsresponsen, og fra dem filterets overføringsfunksjon. Imidlertid er dette i praksis ikke gjennomførbart, siden impulsresponsen til et slikt filter har en uendelig lengde. I tillegg er et slikt filter ikke fysisk realiserbart siden impulsresponsen begynner kl.¥ , og ingen begrenset forsinkelse vil gjøre dette filteret fysisk realiserbart. En mulig metode for å oppnå et FIR-filter som tilnærmer en gitt frekvensrespons er å avkorte den uendelige Fourier-serien og impulsresponsen til filteret, forutsatt at h (n)=0 ved . Deretter Fysisk realiserbarhet av overføringsfunksjonen H(z ) kan oppnås ved å multiplisere H(z) på. Hvor (10.32). Med en slik modifikasjon av overføringsfunksjonen endres ikke amplitudekarakteristikken til filteret, og gruppeforsinkelsen øker med en konstant mengde. Som et eksempel, la oss beregne et lavpass FIR-filter med en frekvensrespons på skjemaet I samsvar med (10.29) er fbeskrevet av uttrykket Nå fra (10.31) kan vi få et uttrykk for overføringsfunksjonen Hvor (10.36). Amplitudekarakteristikker til det beregnede filteret for ulike N er presentert i fig. 10.2.
Fig.10.2 Rippling i passbåndet og stoppbåndet oppstår på grunn av den langsomme konvergensen av Fourier-serien, som igjen er forårsaket av tilstedeværelsen av en diskontinuitet i funksjonen ved grensefrekvensen til passbåndet. Disse pulseringene er kjent som Gibbs krusning. Fra fig. 10.2 er det tydelig at med økende N pulseringsfrekvensen øker og amplituden avtar ved både lavere og høyere frekvenser. Imidlertid forblir amplituden til den siste krusningen i passbåndet og den første krusningen i stoppbåndet praktisk talt uendret. I praksis er slike effekter ofte uønskede, noe som krever å finne måter å redusere Gibbs-pulseringer på. Trunkert impulsrespons h(n ) kan representeres som produktet av den nødvendige uendelige impulsresponsen og noen vindusfunksjoner w (n) av lengde n (fig. 10.3).
I det betraktede tilfellet med enkel trunkering av Fourier-serien, bruker vi rektangulært vindu I dette tilfellet kan frekvensresponsen til filteret representeres som en kompleks konvolusjon Dette betyr at det vil være en "uskarp" versjon av den nødvendige egenskapen. Problemet kommer ned til å finne vindusfunksjoner som gjør det mulig å redusere Gibbs rippel med samme filterselektivitet. For å gjøre dette må du først studere egenskapene til vindusfunksjonen ved å bruke eksemplet med et rektangulært vindu. Spekteret til den rektangulære vindusfunksjonen kan skrives som Spekteret til den rektangulære vindusfunksjonen er presentert i fig. 10.4.
Fig.10.4 Siden ved , viser bredden på hovedloben av spekteret seg å være lik . Tilstedeværelsen av sidelober i spekteret til vindusfunksjonen fører til en økning i Gibbs-rippel i frekvensresponsen til filteret. For å oppnå lav rippel i passbåndet og høy dempning i stoppbåndet, er det nødvendig at arealet begrenset av sidelobene er en liten brøkdel av arealet begrenset av hovedloben. På sin side bestemmer bredden på hovedloben bredden på overgangssonen til det resulterende filteret. For høy filterselektivitet bør bredden på hovedloben være så liten som mulig. Som det fremgår av ovenstående, avtar bredden på hovedloben med økende filterrekkefølge. Dermed kan egenskapene til passende vindusfunksjoner formuleres som følger: - vindusfunksjonen må være begrenset i tid; - spekteret til vindusfunksjonen bør best tilnærme den frekvensbegrensede funksjonen, dvs. ha et minimum av energi utenfor hovedlappen; - Bredden på hovedloben til vindusfunksjonsspekteret bør være så liten som mulig. De mest brukte vindusfunksjonene er: 1. Rektangulært vindu. Diskutert ovenfor. 2. Hammervindu. Hvor . Dette vinduet kalles Hann-vinduet ( hanning). 3. Blackman-vindu. 4. Bartletts vindu. Indikatorene for filtre bygget ved hjelp av de spesifiserte vindusfunksjonene er oppsummert i Tabell 10.1.
Rippelfaktoren er definert som forholdet mellom den maksimale amplituden til sideloben og amplituden til hovedloben i spekteret til vindusfunksjonen. For å velge ønsket filterrekkefølge og den mest hensiktsmessige vindusfunksjonen ved beregning av reelle filtre, kan du bruke dataene i Tabell 10.2.
Som det fremgår av tabell 10.1 er det en viss sammenheng mellom krusningskoeffisienten og bredden på hovedloben i spekteret til vindusfunksjonen. Jo mindre pulsasjonskoeffisienten er, desto større er bredden på hovedloben, og derfor overgangssonen i frekvensresponsen til filteret. For å sikre lav krusning i passbåndet, er det nødvendig å velge et vindu med en passende krusningskoeffisient, og gi den nødvendige bredden på overgangssonen med en økt filterrekkefølge N. Dette problemet kan løses ved å bruke vinduet foreslått av Kaiser. Kaiser-vindusfunksjonen har formen
hvor a er en uavhengig parameter,
En attraktiv egenskap ved Kaiser-vinduet er muligheten til å jevnt endre pulsasjonskoeffisienten fra små til store verdier, mens du bare endrer én parameter a. I dette tilfellet, som for andre vindusfunksjoner, kan bredden på hovedloben justeres med filterrekkefølgen N. De viktigste parameterne som er satt når du utvikler et ekte filter er: Båndbredde - w p; Hinderstripe - w a ; Den maksimale tillatte krusningen i passbåndet er A p ; Minimum stoppbånddempning – A a ; -Prøvetakingsfrekvens - ws. Disse parameterne er illustrert i fig. 10.5. I dette tilfellet bestemmes den maksimale krusningen i passbåndet som
og minimumsdempingen i stoppbåndet er som Den relativt enkle prosedyren for å beregne et filter med et Kaiser-vindu inkluderer følgende trinn: 1. Impulsresponsen til filteret h (n) bestemmes, forutsatt at frekvensresponsen er ideell
hvor (10.49). 2. Parameter d er valgt som
Hvor 3. Den sanne verdien av A a og Ap beregnes ved å bruke formler (10.46), (10.47). 4.Parameter a er valgt som
5.Parameter D er valgt som
6. Velg den minste oddeverdien for filterrekkefølgen fra betingelsen
følger det Siden samplene av impulsresponsen til filteret er koeffisientene til overføringsfunksjonen, betyr betingelse (10.59) at kodene til alle filterkoeffisienter bare inneholder brøkdelen og fortegnsbiten og ikke inneholder heltallsdelen. Antallet sifre i brøkdelen av filterkoeffisientene bestemmes ut fra betingelsen om å tilfredsstille filteroverføringsfunksjonen med kvantiserte koeffisienter, de spesifiserte kravene for å nærme seg referanseoverføringsfunksjonen med eksakte verdier av koeffisientene. De absolutte verdiene til filterinngangssignalsamplene er vanligvis normalisert slik at Hvis analysen utføres for et FIR-filter med en lineær faserespons, kan algoritmen for å beregne utgangssignalet være som følger hvor er filterkoeffisientene avrundet til s k. Denne algoritmen tilsvarer filterblokkdiagrammet vist i fig. 10.5.
Det er to måter å implementere denne algoritmen på. I det første tilfellet utføres alle multiplikasjonsoperasjoner nøyaktig og det er ingen avrunding av produkter. I dette tilfellet er bitdybden til produktene lik s i +s k, der s in er bitdybden til inngangssignalet, og s k er bitdybden til filterkoeffisientene. I dette tilfellet tilsvarer blokkskjemaet til filteret vist i fig. 10.5 nøyaktig det virkelige filteret. I den andre metoden for å implementere algoritmen (10.61) blir hvert resultat av multiplikasjonsoperasjonen avrundet, dvs. produkter er beregnet med noen feil. I dette tilfellet er det nødvendig å endre algoritmen (10.61) for å ta hensyn til feilen introdusert ved å avrunde produktene Hvis prøveverdiene til filterutgangssignalet beregnes ved hjelp av den første metoden (med eksakte verdier av produktene), bestemmes spredningen av utgangsstøyen som
de. avhenger av variansen til avrundingsstøyen til inngangssignalet og verdiene til filterkoeffisientene. Herfra kan du finne det nødvendige antallet biter av inngangssignalet som
Ved å bruke de kjente verdiene for s in og s k, kan man bestemme antall biter som kreves for brøkdelen av utgangssignalkoden som Hvis verdiene til utgangssignalprøvene beregnes ved hjelp av den andre metoden, når hvert produkt er avrundet til s d sifre, kan spredningen av avrundingsstøyen som skapes av hver av multiplikatorene uttrykkes i form av sifferkapasiteten til produkt som DR inn og signal-til-støy-forhold ved filterutgangen SNR ut. Det dynamiske området til inngangssignalet i desibel er definert som
hvor A max og A min er maksimums- og minimumsamplitudene til filterinngangssignalet. Signal-til-støy-forholdet ved filterutgangen, uttrykt i desibel, er definert som
bestemmer rotmiddelverdien til kraften til utgangssinusformet signal fra filteret med amplitude A min, og (10.77) bestemmer støyeffekten ved filterutgangen. Fra (10.75) og (10.76) med A max =1 får vi et uttrykk for spredningen av filterutgangsstøyen Denne filterutgangsstøyspredningsverdien kan brukes til å beregne bitdybden til filterets inngangs- og utgangssignaler.  En verden av gratis programmer og nyttige tips 2024 whatsappss.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(10.2),
- amplitude-frekvensrespons (AFC) filter,
- fase-frekvensrespons (PFC) filter.
(10.3).
(10.4).
(10.6).
(10.7).
(10.8).
(10.9).
(10.10).
(10.12).
(10.17).
(10.19),
(10.20).
(10.21).
(10.22).
(10.23).
(10.25),
(10.26).
(10.27).
(10.28),
(10.29).
(10.30).
(10.31),
(10.33).
(10.34).
(10.35),
(10.37).
(10.38).
(10.39).
(10.40).
(10.41),
(10.42).
(10.43).
(10.44),
, I 0 – Bessel-funksjon av den første typen nullorden, definert av uttrykket
(10.45).
(10.46),
(10.50),
(10.51).
(10.52).
(10.53).
(10.54),
(10.57)
(10.66),
(10.67).
(10.74),
(10.75),
(10.78).