การตอบสนองแบบอิมพัลส์ของตัวกรอง ฟิลเตอร์ดิจิตอลพร้อมการตอบสนองอิมพัลส์จำกัด การปรับข้อมูลให้เรียบ การกรองค่ามัธยฐาน
ฟิลเตอร์ดิจิตอล 48 ตัวพร้อมการตอบสนองอิมพัลส์จำกัด การคำนวณตัวกรอง kih
ตัวกรองการตอบสนองแรงกระตุ้นจำกัด (ตัวกรองแบบไม่เรียกซ้ำ, ตัวกรองเฟอร์) หรือตัวกรอง FIR (FIR ย่อมาจาก การตอบสนองแรงกระตุ้นอัน จำกัด - การตอบสนองแรงกระตุ้นอัน จำกัด ) - หนึ่งในประเภทของตัวกรองดิจิทัลเชิงเส้นซึ่งเป็นคุณลักษณะเฉพาะที่มีการ จำกัด เวลา การตอบสนองแรงกระตุ้น(จากจุดหนึ่ง มันจะเท่ากับศูนย์ทุกประการ) ตัวกรองดังกล่าวเรียกอีกอย่างว่าไม่เรียกซ้ำเนื่องจากขาดคำติชม ตัวหารของฟังก์ชันการถ่ายโอนของตัวกรองดังกล่าวคือค่าคงที่ที่แน่นอน
สมการผลต่างที่อธิบายความสัมพันธ์ระหว่างสัญญาณอินพุตและเอาต์พุตของตัวกรอง: โดยที่ ป- ลำดับการกรอง x(n) - สัญญาณอินพุต ย(n) คือสัญญาณเอาท์พุต และ ข ฉัน- ค่าสัมประสิทธิ์การกรอง กล่าวอีกนัยหนึ่ง ค่าของตัวอย่างสัญญาณเอาท์พุตใดๆ จะถูกกำหนดโดยผลรวมของค่าที่ปรับขนาดได้ ปการอ่านครั้งก่อน คุณสามารถพูดได้แตกต่างออกไป: ค่าของเอาต์พุตตัวกรอง ณ เวลาใดก็ได้คือค่าของการตอบสนองต่อค่าทันทีของอินพุตและผลรวมของการตอบสนองที่ค่อยๆ ลดลงทั้งหมด ปตัวอย่างสัญญาณก่อนหน้าที่ยังคงส่งผลต่อเอาท์พุต (หลัง ป-นับ ฟังก์ชั่นการเปลี่ยนพัลส์จะเท่ากับศูนย์ดังที่ได้กล่าวไปแล้ว ดังนั้นเงื่อนไขทั้งหมดหลังจากนั้น ป-th ก็จะเท่ากับศูนย์ด้วย) มาเขียนสมการก่อนหน้าในรูปแบบที่มีความจุมากขึ้น:
เพื่อค้นหาเคอร์เนลตัวกรองที่เราใส่
x(n) = δ( n)
โดยที่ δ( n) - ฟังก์ชันเดลต้า จากนั้นการตอบสนองแบบอิมพัลส์ของตัวกรอง FIR สามารถเขียนได้เป็น:
การแปลงรูป Z ของการตอบสนองแบบอิมพัลส์ทำให้เรามีฟังก์ชันการถ่ายโอนของตัวกรอง FIR:
]คุณสมบัติ
ตัวกรอง FIR มีคุณสมบัติที่เป็นประโยชน์หลายประการ ซึ่งทำให้บางครั้งควรใช้ตัวกรองมากกว่าตัวกรอง IIR นี่คือบางส่วนของพวกเขา:
ตัวกรอง FIR มีความทนทาน
ตัวกรอง FIR ไม่ต้องการผลตอบรับเมื่อนำไปใช้งาน
เฟสของตัวกรอง FIR สามารถทำให้เป็นเส้นตรงได้
รูปแบบตรงของตัวกรอง FIR
ตัวกรอง FIR สามารถนำมาใช้ได้โดยใช้องค์ประกอบสามประการ ได้แก่ ตัวคูณ ตัวบวก และบล็อกการหน่วงเวลา ตัวเลือกที่แสดงในรูปคือการใช้งานตัวกรอง FIR ประเภท 1 โดยตรง
การใช้รูปแบบโดยตรงของตัวกรอง FIR
ตัวอย่างโปรแกรม
ด้านล่างนี้เป็นตัวอย่างโปรแกรมกรอง FIR ที่เขียนด้วยภาษา C:
/* ฟิลเตอร์ FIR 128 ก๊อก */
float fir_filter (อินพุตลอย)
ตัวอย่างลอยคงที่
ตามมาตรฐาน = 0.0f; /* แบตเตอรี่ */
/* คูณและสะสม */
สำหรับ (i = 0; i< 128; i++) {
ตามมาตรฐาน += (h[i] * ตัวอย่าง[i]);
/* ออก */
/* เลื่อนสัญญาณดีเลย์ */
สำหรับ (i = 127; i > 0; i--)
ตัวอย่าง[i] = ตัวอย่าง;
49 การปรับข้อมูลให้เรียบ ค่าเฉลี่ยเคลื่อนที่
50 การปรับข้อมูลให้เรียบ การปรับให้เรียบแบบพาราโบลา
51 การปรับข้อมูลให้เรียบ สเปนเซอร์ ปรับให้เรียบ
52 การปรับข้อมูลให้เรียบ การกรองค่ามัธยฐาน
ค่าเฉลี่ยเคลื่อนที่, การปรับให้เรียบแบบพาราโบลา, การปรับให้เรียบของสเปนเซอร์, การกรองค่ามัธยฐาน
เมื่อพัฒนาวิธีการกำหนดพารามิเตอร์ของกระบวนการทางกายภาพที่เปลี่ยนแปลงอย่างช้าๆ เมื่อเวลาผ่านไป งานสำคัญคือการขจัดอิทธิพลของเสียงรบกวนหรือการรบกวนแบบสุ่มที่ทับบนสัญญาณประมวลผลที่ได้รับที่เอาต์พุตของตัวแปลงหลัก
หากต้องการกำจัดผลกระทบนี้ คุณสามารถใช้การปรับข้อมูลให้เรียบได้ วิธีที่ง่ายที่สุดวิธีหนึ่งในการปรับให้เรียบคือการหาค่าเฉลี่ยเลขคณิต เมื่อใช้งาน แต่ละค่าของฟังก์ชันแยก (อาร์เรย์ข้อมูลที่ประมวลผล) จะถูกคำนวณตามนิพจน์:
โดยที่จำนวนคะแนนสำหรับการหาค่าเฉลี่ยเลขคณิต (จำนวนเต็มคี่)
ค่าของฟังก์ชันก่อนการประมวลผล
มีวิธีการอื่น ๆ ที่ค่อนข้างมีประสิทธิภาพในการปรับให้เรียบ ตัวอย่างเช่น ด้วยพาราโบลาของระดับที่สองที่ห้า, เจ็ด, เก้าและสิบเอ็ดจุดตามนิพจน์:
หรือพาราโบลาระดับที่สี่ที่เจ็ด เก้า สิบเอ็ด และสิบสามจุด:
ในการใช้งานจริง วิธีการที่มีประสิทธิภาพอื่นๆ เช่น การปรับให้เรียบ Spencer 15 จุด ให้ผลลัพธ์ที่ดี:
โดยการแทนที่เลขชี้กำลังเชิงซ้อน ซึ่งในนิพจน์เหล่านี้ เราสามารถกำหนดฟังก์ชันถ่ายโอนของการแปลงที่สอดคล้องกันได้
สำหรับการหาค่าเฉลี่ยเลขคณิต
นิพจน์ในวงเล็บแสดงถึงความก้าวหน้าทางเรขาคณิตที่มีตัวส่วน ดังนั้นนิพจน์นี้สามารถแสดงได้เป็น:
.
สูตรนี้แสดงถึงคุณลักษณะการถ่ายโอนของตัวกรองความถี่ต่ำผ่าน และแสดงให้เห็นว่า ยิ่งมีเงื่อนไขที่เกี่ยวข้องกับการหาค่าเฉลี่ยมากเท่าใด การปราบปรามส่วนประกอบสัญญาณรบกวนความถี่สูงในสัญญาณก็จะยิ่งมากขึ้นเท่านั้น (ดูรูปที่ 6.1)
อย่างไรก็ตาม แนวคิดเชิงความหมายของความถี่เมื่อประมวลผลแนวโน้มเวลาแตกต่างจากแนวคิดที่คล้ายกันเมื่อประมวลผลสัญญาณ สิ่งนี้อธิบายได้จากข้อเท็จจริงที่ว่าเมื่อศึกษาแนวโน้มของเวลา ไม่ใช่องค์ประกอบความถี่ที่น่าสนใจ แต่เป็นประเภทของการเปลี่ยนแปลง (เพิ่มขึ้น ลดลง ความคงที่ วงจร ฯลฯ )
การใช้สิ่งที่เรียกว่าอัลกอริธึมฮิวริสติกยังค่อนข้างมีประสิทธิภาพในการปรับข้อมูลให้เรียบ
หนึ่งในนั้นคือการกรองค่ามัธยฐาน ในระหว่างการนำไปใช้ในหน้าต่างเวลาเลื่อนของมิติ โดยที่จำนวนเต็มเป็นเลขคี่ องค์ประกอบกลางจะถูกแทนที่ด้วยองค์ประกอบตรงกลางของลำดับ ซึ่งเรียงลำดับจากน้อยไปมากของค่า องค์ประกอบของอาร์เรย์ข้อมูลของการเรียบ สัญญาณตกภายในกรอบเวลา ข้อดีของการกรองค่ามัธยฐานคือความสามารถในการกำจัดสัญญาณรบกวนแบบอิมพัลส์ ซึ่งมีระยะเวลาไม่เกิน โดยแทบไม่มีการบิดเบือนของสัญญาณที่เปลี่ยนแปลงอย่างราบรื่น วิธีการลดเสียงรบกวนนี้ไม่มีเหตุผลทางคณิตศาสตร์ที่เข้มงวด แต่ความเรียบง่ายของการคำนวณและประสิทธิผลของผลลัพธ์ที่ได้นำไปสู่การใช้อย่างแพร่หลาย
รูปที่ 6.1 - กราฟคุณลักษณะการถ่ายโอน
การดำเนินการหาค่าเฉลี่ยเลขคณิตสำหรับ m=5, 7, 9, 11
อัลกอริธึมการปรับให้เรียบที่น่าสนใจอีกประการหนึ่งคือค่ามัธยฐานเฉลี่ย สาระสำคัญของมันมีดังนี้ ในหน้าต่างเวลาเลื่อนที่มีขนาด (-จำนวนเต็มคี่) องค์ประกอบของอาร์เรย์ข้อมูลจะถูกเรียงลำดับจากน้อยไปมาก จากนั้นองค์ประกอบแรกและสุดท้ายจะถูกลบออกจากลำดับการสั่งซื้อ (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
วิธีนี้ช่วยให้คุณระงับการรบกวนของพัลส์และความถี่วิทยุ รวมถึงการปรับสัญญาณให้ราบรื่นดี
| " |
พิจารณาตัวกรองดิจิทัลที่ง่ายที่สุด - ตัวกรองที่มีพารามิเตอร์คงที่
สัญญาณอินพุตของตัวกรองดิจิทัลจะถูกป้อนในรูปแบบของลำดับค่าตัวเลขตามช่วงเวลา (รูปที่ 4.1, a) เมื่อได้รับค่าสัญญาณถัดไปแต่ละค่าในตัวกรองดิจิทัล ค่าถัดไปของสัญญาณเอาต์พุตจะถูกคำนวณ อัลกอริธึมการคำนวณสามารถมีความหลากหลายมาก ในระหว่างขั้นตอนการคำนวณ สามารถใช้ค่าสุดท้ายของสัญญาณอินพุตได้
ค่าก่อนหน้าของสัญญาณอินพุตและเอาต์พุต: สัญญาณเอาท์พุตของตัวกรองดิจิทัลยังเป็นลำดับของค่าตัวเลขตามช่วงเวลาของ ช่วงเวลานี้จะเท่ากันสำหรับอุปกรณ์ประมวลผลสัญญาณดิจิทัลทั้งหมด
ข้าว. 4.1. สัญญาณที่อินพุตและเอาต์พุตของตัวกรองดิจิทัล
ดังนั้นหากคุณใช้สัญญาณที่ง่ายที่สุดในรูปของพัลส์เดี่ยวกับอินพุตของตัวกรองดิจิทัล (รูปที่ 4.2, a)
จากนั้นที่เอาต์พุตเราจะได้สัญญาณในรูปแบบของลำดับค่าตัวเลขที่ไม่ต่อเนื่องตามช่วงเวลา
โดยการเปรียบเทียบกับวงจรแอนะล็อกทั่วไป เราจะเรียกสัญญาณตอบสนองนี้ว่าการตอบสนองแบบอิมพัลส์ของตัวกรอง (รูปที่ 4.2, b) ต่างจากการตอบสนองแบบอิมพัลส์ของวงจรแอนะล็อก ฟังก์ชันนี้ไม่มีมิติ
ข้าว. 4.2. หน่วยการตอบสนองแรงกระตุ้นและแรงกระตุ้นของตัวกรองดิจิทัล
ให้เราใช้สัญญาณแยกตามอำเภอใจกับอินพุตตัวกรอง (รูปที่. 4.1,a) ซึ่งเป็นชุดของค่าที่ไม่ต่อเนื่องกัน
ภายใต้การกระทำขององค์ประกอบแรก ลำดับคูณด้วยจะเกิดขึ้นที่เอาท์พุตของตัวกรอง ภายใต้การกระทำ ลำดับจะถูกคูณด้วยและเลื่อนไปทางขวาด้วยจำนวน ฯลฯ ด้วยเหตุนี้ ผลลัพธ์ที่ได้จะได้รับ ลำดับที่ไหน
ดังนั้นสัญญาณเอาท์พุตจึงถูกกำหนดให้เป็นการบิดแยกของสัญญาณอินพุตและการตอบสนองแบบอิมพัลส์ ในส่วนนี้ ตัวกรองดิจิทัลจะคล้ายกับวงจรทั่วไป โดยที่สัญญาณเอาท์พุตจะเท่ากับการบิดของสัญญาณอินพุตและการตอบสนองแบบอิมพัลส์
สูตร (4.1) เป็นอัลกอริธึมการกรองแบบดิจิทัล หากการตอบสนองแบบอิมพัลส์ของตัวกรองถูกอธิบายตามลำดับที่มีเงื่อนไขจำนวนจำกัด ตัวกรองนั้นสามารถนำไปใช้ในรูปแบบของวงจรที่แสดงในรูปที่ 1 4.3. ในที่นี้ตัวอักษรจะระบุองค์ประกอบของการหน่วงเวลาของสัญญาณ (ต่อเซลล์) - องค์ประกอบที่คูณสัญญาณด้วยค่าสัมประสิทธิ์ที่สอดคล้องกัน
แผนภาพที่แสดงในรูปที่. 4.3 ไม่ใช่วงจรไฟฟ้าของตัวกรองดิจิทัล แผนภาพนี้เป็นการแสดงภาพกราฟิกของอัลกอริธึมการกรองดิจิทัล และแสดงลำดับการดำเนินการทางคณิตศาสตร์ที่ดำเนินการระหว่างการประมวลผลสัญญาณ
ข้าว. 4.3. วงจรกรองดิจิตอลแบบไม่เรียกซ้ำ
สำหรับตัวกรองดิจิทัลที่ประมวลผลสัญญาณในรูปแบบของลำดับตัวเลขเชิงนามธรรม แนวคิดเรื่อง "การหน่วงเวลา" นั้นไม่ถูกต้องทั้งหมด ดังนั้นองค์ประกอบที่หน่วงเวลาสัญญาณหนึ่งเซลล์มักจะถูกทำเครื่องหมายบนวงจรตัวกรองดิจิทัลพร้อมสัญลักษณ์ที่บ่งบอกถึงการหน่วงเวลาของสัญญาณในภาษาของ -การเปลี่ยนแปลง ต่อไปนี้เราจะยึดตามสัญกรณ์นี้
กลับไปที่วงจรกรองดิจิตอลดังแสดงในรูปที่ 1 4.3 ตัวกรองดังกล่าวซึ่งใช้เฉพาะค่าของสัญญาณอินพุตในการคำนวณเรียกว่าแบบง่ายหรือแบบไม่เรียกซ้ำ
อัลกอริธึมตัวกรองแบบไม่เรียกซ้ำนั้นง่ายต่อการเขียนหากทราบการตอบสนองแบบอิมพัลส์ของตัวกรอง สำหรับการใช้งานอัลกอริธึมในทางปฏิบัติ การตอบสนองแบบอิมพัลส์จำเป็นต้องมีคำศัพท์จำนวนจำกัด หากการตอบสนองแบบอิมพัลส์มีจำนวนคำศัพท์ไม่ จำกัด แต่ค่าจะลดลงอย่างรวดเร็วคุณสามารถ จำกัด ตัวเองให้อยู่ในจำนวนที่ จำกัด โดยละทิ้งคำศัพท์ที่มีค่าน้อย หากองค์ประกอบของการตอบสนองแบบอิมพัลส์ไม่ลดค่าลง อัลกอริธึมตัวกรองแบบไม่เรียกซ้ำจะกลายเป็นไม่สามารถรับรู้ได้
ข้าว. 4.4. -โซ่
ตัวอย่างเช่นให้พิจารณาตัวกรองดิจิทัลที่ง่ายที่สุดซึ่งคล้ายกับวงจร (รูปที่ 4.4) การตอบสนองแบบอิมพัลส์ของวงจรมีรูปแบบ
ในการเขียนการตอบสนองแบบอิมพัลส์ของตัวกรองดิจิทัลที่สอดคล้องกัน ควรแทนที่นิพจน์ด้วย อย่างไรก็ตาม การตอบสนองแบบอิมพัลส์ของวงจรจะมีมิติ และการตอบสนองแบบอิมพัลส์ของตัวกรองดิจิทัลจะต้องไม่มีมิติ ดังนั้นเราจึงละเว้นตัวคูณในนิพจน์ (4.2) และเขียนการตอบสนองแบบอิมพัลส์ของตัวกรองดิจิทัลในรูปแบบ
การตอบสนองแบบกระตุ้นนั้นประกอบด้วยพจน์มากมายนับไม่ถ้วน แต่ขนาดของพวกมันจะลดลงตามกฎเลขเอ็กซ์โพเนนเชียล และเราสามารถจำกัดตัวเองอยู่แค่เงื่อนไข โดยเลือกเช่นนั้น
ตอนนี้เราสามารถเขียนนิพจน์สำหรับสัญญาณที่เอาต์พุตตัวกรองได้
นิพจน์นี้เป็นอัลกอริธึมตัวกรองดิจิทัลด้วย แผนภาพของตัวกรองนี้แสดงในรูปที่ 1 4.5.
วิธีที่สองในการวิเคราะห์กระบวนการในตัวกรองดิจิทัลนั้นคล้ายคลึงกับวิธีดำเนินการในการวิเคราะห์วงจรแอนะล็อกทั่วไป แทนที่จะใช้การแปลง Laplace เท่านั้น จะใช้ -transform แทน
ข้าว. 4.5. วงจรของตัวกรองดิจิทัลแบบไม่เรียกซ้ำคล้ายกับวงจร
เรามากำหนดพารามิเตอร์ตัวกรองดิจิทัลที่คล้ายกับฟังก์ชันการถ่ายโอนของวงจรไฟฟ้า เมื่อต้องการทำเช่นนี้ ให้ใช้การแปลงกับการตอบสนองแบบอิมพัลส์ของตัวกรองดิจิทัล:
ฟังก์ชันนี้เรียกว่าฟังก์ชันตัวกรองระบบ
ตามนิพจน์ (4.1) สัญญาณที่เอาต์พุตของตัวกรองดิจิทัลจะเท่ากับการบิดแยกของสัญญาณอินพุตและการตอบสนองแบบอิมพัลส์ของตัวกรอง เมื่อใช้ทฤษฎีบทการบิดกับนิพจน์นี้ เราได้มาว่าการแปลงสัญญาณเอาท์พุตเท่ากับการแปลงสัญญาณอินพุตคูณด้วยฟังก์ชันตัวกรองระบบ:
ดังนั้นฟังก์ชันระบบจึงมีบทบาทเป็นฟังก์ชันถ่ายโอนข้อมูลของตัวกรองดิจิทัล
ตัวอย่างเช่น ลองค้นหาฟังก์ชันระบบของตัวกรองดิจิทัลลำดับที่หนึ่งที่คล้ายกับ -circuit:
วิธีที่สามในการวิเคราะห์การส่งผ่านสัญญาณผ่านตัวกรองดิจิทัลนั้นคล้ายคลึงกับวิธีดั้งเดิมของสมการเชิงอนุพันธ์ ลองพิจารณาวิธีนี้โดยใช้กลุ่มการสั่งซื้อเป็นตัวอย่าง
วงจรแอนะล็อกที่ง่ายที่สุดลำดับที่ 1 คือ -วงจร (ดูรูปที่ 4.4) ซึ่งเป็นเส้นทางผ่านของสัญญาณซึ่งอธิบายโดยสมการเชิงอนุพันธ์
สำหรับวงจรแยกแทนที่จะเป็นสมการเชิงอนุพันธ์ (4.8) ควรเขียนสมการความแตกต่างโดยระบุสัญญาณอินพุตและเอาต์พุตสำหรับช่วงเวลาที่ไม่ต่อเนื่องและแทนที่จะเป็นอนุพันธ์ควรใช้ความแตกต่างของค่าสัญญาณที่อยู่ติดกัน ปรากฏ. สำหรับวงจรลำดับที่ 1 แบบแยก สมการผลต่างสามารถเขียนได้ในรูปแบบทั่วไป
ลองใช้การแปลงกับสมการกัน
โดยที่เราพบฟังก์ชันตัวกรองระบบ
สูตร (4.10) เป็นนิพจน์ทั่วไปสำหรับฟังก์ชันระบบของตัวกรองดิจิทัลลำดับที่ 1 เมื่อมันเกิดขึ้นพร้อมกับนิพจน์ที่ได้รับก่อนหน้านี้ (4.7) สำหรับฟังก์ชันระบบของตัวกรองดิจิทัลที่เทียบเท่ากับ -วงจร
ให้เราค้นหาอัลกอริธึมการกรองดิจิทัลที่สอดคล้องกับฟังก์ชันระบบ (4.10) เมื่อต้องการทำเช่นนี้ เราจะแก้สมการ (4.9) เพื่อ
แผนภาพที่เทียบเท่าของอัลกอริธึมนี้แสดงไว้ในรูปที่ 1 4.6. เมื่อเปรียบเทียบกับตัวกรองแบบไม่เรียกซ้ำ (ดูรูปที่ 4.5) มีการเพิ่ม "วงจรป้อนกลับ" ชนิดหนึ่งซึ่งหมายความว่าค่าของสัญญาณเอาท์พุตจะถูกใช้ในภายหลัง
ข้าว. 4.6. วงจรของตัวกรองดิจิทัลแบบเรียกซ้ำคล้ายกับวงจร
การคำนวณ ตัวกรองประเภทนี้เรียกว่าแบบเรียกซ้ำ
อัลกอริทึม (4.11) สอดคล้องกับตัวกรองที่เทียบเท่ากับตัวกรองแบบไม่เรียกซ้ำที่พิจารณาก่อนหน้านี้โดยสมบูรณ์ แต่ในการกำหนดค่าหนึ่งค่าของสัญญาณเอาท์พุตโดยใช้อัลกอริธึมตัวกรองแบบไม่เรียกซ้ำ (4.4) จำเป็นต้องดำเนินการและเมื่อใช้อัลกอริธึมตัวกรองแบบเรียกซ้ำ (4.11) จำเป็นต้องมีการดำเนินการเพียงสองครั้งเท่านั้น นี่คือข้อได้เปรียบหลักของตัวกรองแบบเรียกซ้ำ นอกจากนี้ ตัวกรองแบบเรียกซ้ำยังช่วยให้การประมวลผลสัญญาณมีความแม่นยำสูงขึ้น เนื่องจากตัวกรองเหล่านี้ช่วยให้การดำเนินการตอบสนองอิมพัลส์ถูกต้องมากขึ้นโดยไม่ต้องละทิ้ง "ส่วนท้าย" ตัวกรองแบบเรียกซ้ำช่วยให้คุณสามารถใช้อัลกอริทึมที่ไม่สามารถนำมาใช้ได้เลยโดยใช้ตัวกรองที่ไม่เรียกซ้ำ ตัวอย่างเช่น ตัวกรองทำงานตามวงจรในรูป 4.6 โดยพื้นฐานแล้วเป็นตัวสะสม-รวมระบบในอุดมคติและมีการตอบสนองแบบอิมพัลส์ของตัวกรองรูปแบบ A ที่มีคุณสมบัติดังกล่าวไม่สามารถนำมาใช้ได้โดยใช้รูปแบบที่ไม่เกิดซ้ำ
ตัวอย่างที่พิจารณาแสดงให้เห็นว่าไม่มีประโยชน์ในการใช้อัลกอริธึมที่ไม่เรียกซ้ำเพื่อสร้างตัวกรองดิจิทัลที่มีการตอบสนองแบบอิมพัลส์ที่ยาว ในกรณีเหล่านี้ การใช้ตัวกรองแบบเรียกซ้ำจะเหมาะสมกว่า
ขอบเขตการใช้งานของอัลกอริธึมแบบไม่เรียกซ้ำคือการใช้ตัวกรองดิจิทัลพร้อมการตอบสนองแบบอิมพัลส์ที่มีคำศัพท์จำนวนน้อย ตัวอย่างคือตัวสร้างความแตกต่างที่ง่ายที่สุด โดยสัญญาณเอาท์พุตจะเท่ากับการเพิ่มขึ้นของสัญญาณอินพุต:
วงจรของตัวกรองดิจิทัลดังกล่าวจะแสดงในรูปที่ 1 4.7.
ข้าว. 4.7. วงจรของตัวสร้างความแตกต่างทางดิจิทัลที่ง่ายที่สุด
ให้เราพิจารณาตัวกรองดิจิทัลทั่วไปซึ่งอธิบายโดยสมการ
สมการนี้ถือได้ว่าเป็นสมการผลต่างของลำดับและเป็นอัลกอริธึมการกรองแบบดิจิทัลหากเขียนใหม่ต่างกัน กล่าวคือ
ข้าว. 4.8. วงจรกรองลำดับดิจิทัลแบบเรียกซ้ำ
อัลกอริทึม (4.13) สอดคล้องกับวงจรที่แสดงในรูปที่ 1 4.8. ให้เราค้นหาฟังก์ชั่นระบบของตัวกรองดังกล่าว เมื่อต้องการทำเช่นนี้ ให้ใช้การแปลงกับสมการ:
นิพจน์ (4.14) ช่วยให้เราสามารถสร้างการเชื่อมต่อระหว่างความผันผวนขององค์ประกอบของวงจรตัวกรองและฟังก์ชันของระบบได้ ค่าสัมประสิทธิ์ในตัวเศษของฟังก์ชันระบบจะกำหนดค่าของสัมประสิทธิ์สำหรับ
(ในส่วนที่ไม่เกิดซ้ำของตัวกรอง) และค่าสัมประสิทธิ์ในตัวส่วนจะกำหนดส่วนที่เกิดซ้ำของตัวกรอง
ทุกอย่างเริ่มต้นเมื่อเพื่อนของเพื่อนของเพื่อนต้องการความช่วยเหลือเกี่ยวกับตัวกรองเดียวกันนี้ ตามแนวทางของเจได ข่าวลือเกี่ยวกับเรื่องนี้มาถึงฉัน ฉันยกเลิกการสมัครรับความคิดเห็นในโพสต์ที่ลิงก์ ดูเหมือนว่าจะช่วยได้ ฉันหวังว่า
เรื่องราวนี้ปลุกเร้าความทรงจำเกี่ยวกับเรื่องที่สามหรือบางอย่างในทำนองนั้น เมื่อฉันรับ DSP ด้วยตัวเอง และกระตุ้นให้ฉันเขียนบทความสำหรับทุกคนที่สนใจวิธีการทำงานของตัวกรองดิจิทัล แต่โดยธรรมชาติแล้วกลับรู้สึกหวาดกลัวกับตัวกรองดิจิทัล - สุดยอดสูตรและภาพวาดหลอนๆ (ฉันไม่ได้พูดถึงตำราเรียนอยู่แล้ว)
โดยทั่วไปจากประสบการณ์ของฉัน สถานการณ์ในหนังสือเรียนอธิบายได้ด้วยวลีที่รู้จักกันดีว่าบางครั้งคุณไม่สามารถมองเห็นป่าสำหรับต้นไม้ได้ และกล่าวคือ เมื่อพวกเขาเริ่มทำให้คุณกลัวทันทีด้วยการแปลงรูป Z และสูตรสำหรับการหารพหุนาม ซึ่งมักจะยาวกว่าสองกระดาน ความสนใจในหัวข้อนี้ก็จะหมดไปอย่างรวดเร็วมาก เราจะเริ่มต้นด้วยสิ่งง่ายๆ โชคดีที่เพื่อที่จะเข้าใจสิ่งที่เกิดขึ้น ไม่จำเป็นต้องอธิบายสำนวนที่ซับซ้อนยาวๆ เลย
ก่อนอื่น แนวคิดพื้นฐานง่ายๆ บางประการ
1. การตอบสนองแบบแรงกระตุ้น
สมมติว่าเรามีกล่องที่มีสี่พิน เราไม่รู้ว่ามีอะไรอยู่ข้างใน แต่เรารู้แน่ว่าอาคารผู้โดยสารด้านซ้ายสองแห่งคือทางเข้า และอีกสองแห่งทางด้านขวาคือทางออก ลองใช้พัลส์สั้นมากที่มีแอมพลิจูดขนาดใหญ่มากกับมันแล้วดูว่าเกิดอะไรขึ้นที่เอาท์พุต ยังไม่ชัดเจนว่ามีอะไรอยู่ในจตุรัสนี้ เพราะไม่รู้จะอธิบายอย่างไร แต่อย่างน้อยเราก็จะได้เห็นอะไรบางอย่าง
ในที่นี้ต้องบอกว่าพัลส์ขนาดสั้น (โดยทั่วไปคือสั้นอนันต์) ที่มีแอมพลิจูดขนาดใหญ่ (โดยทั่วไปคืออนันต์) ในทางทฤษฎีเรียกว่าฟังก์ชันเดลต้า อย่างไรก็ตาม สิ่งที่ตลกก็คืออินทิกรัลของสิ่งนี้ ไม่มีที่สิ้นสุดฟังก์ชั่นมีค่าเท่ากับหนึ่ง นี่คือการทำให้เป็นมาตรฐาน
ดังนั้นสิ่งที่เราเห็นที่เอาต์พุตของเครือข่ายควอดริโพลซึ่งใช้ฟังก์ชันเดลต้ากับอินพุตเรียกว่า การตอบสนองแรงกระตุ้นสี่เหลี่ยมนี้ อย่างไรก็ตาม ในตอนนี้ยังไม่ชัดเจนว่าจะช่วยเราได้อย่างไร แต่ให้เราจำผลลัพธ์ที่ได้รับและไปยังแนวคิดที่น่าสนใจถัดไป
2. การบิดตัว
กล่าวโดยสรุป การบิดเป็นการดำเนินการทางคณิตศาสตร์ที่มาจากการรวมผลคูณของฟังก์ชัน:
อย่างที่คุณเห็นมีเครื่องหมายดอกจันกำกับไว้ นอกจากนี้คุณยังสามารถเห็นได้ว่าในระหว่างการบิด ฟังก์ชันหนึ่งจะเรียงลำดับ "ไปข้างหน้า" และเราจะดำเนินการฟังก์ชันที่สอง "กลับไปด้านหน้า" แน่นอน ในกรณีที่ไม่ต่อเนื่องซึ่งมีคุณค่ามากกว่าสำหรับมนุษยชาติ การบิดงอก็เหมือนกับอินทิกรัลอื่นๆ ที่จะเข้าสู่การสรุป:
ดูเหมือนเป็นนามธรรมทางคณิตศาสตร์ที่น่าเบื่อ อย่างไรก็ตาม ในความเป็นจริง มัดอาจเป็นปรากฏการณ์ที่มหัศจรรย์ที่สุดในโลกนี้ รองลงมาคือความอัศจรรย์ต่อการเกิดของบุคคล สิ่งเดียวที่แตกต่างคือคนส่วนใหญ่จะรู้ว่าเด็กมาจากไหนอย่างน้อยที่สุดเมื่ออายุมากขึ้น สิบแปด ในขณะที่เกี่ยวกับสิ่งที่บิดเบี้ยวคืออะไรและเหตุใดมันจึงมีประโยชน์และน่าทึ่ง แต่ประชากรส่วนใหญ่ของโลกไม่มีความคิดเลยตลอดชีวิต
ดังนั้นพลังของการดำเนินการนี้อยู่ที่ว่าถ้า f เป็นสัญญาณอินพุตใด ๆ โดยพลการและ g คือการตอบสนองแบบอิมพัลส์ของเครือข่ายสี่พอร์ตผลลัพธ์ของการบิดของฟังก์ชันทั้งสองนี้จะคล้ายกับสิ่งที่เราจะทำ ได้รับโดยการส่งสัญญาณ f ผ่านเครือข่ายสี่พอร์ตนี้
นั่นคือการตอบสนองแบบอิมพัลส์นั้นเป็นคุณสมบัติที่สมบูรณ์ของเครือข่ายสี่พอร์ตที่เกี่ยวข้องกับเอฟเฟกต์อินพุตและการบิดสัญญาณอินพุตทำให้สามารถกู้คืนสัญญาณเอาต์พุตที่สอดคล้องกันได้ ในความคิดของฉัน นี่มันน่าทึ่งมาก!
3. ตัวกรอง
คุณสามารถทำสิ่งที่น่าสนใจมากมายด้วยการตอบสนองแบบกระตุ้นและการบิดตัว ตัวอย่างเช่น หากสัญญาณเป็นเสียง คุณสามารถจัดระเบียบเสียงก้อง เสียงสะท้อน คอรัส แฟลงเจอร์ และอื่นๆ อีกมากมาย คุณสามารถแยกแยะและบูรณาการ... โดยทั่วไป คุณสามารถสร้างอะไรก็ได้ สำหรับเราตอนนี้ สิ่งที่สำคัญที่สุดคือ แน่นอนว่า ตัวกรองสามารถหาได้อย่างง่ายดายโดยใช้การบิด
ตัวกรองดิจิทัลนั้นเป็นการบิดของสัญญาณอินพุตพร้อมการตอบสนองแบบอิมพัลส์ที่สอดคล้องกับตัวกรองที่ต้องการ
แต่แน่นอนว่าต้องได้รับการตอบสนองแบบกระตุ้น แน่นอนว่าเราได้คิดวิธีการวัดค่าข้างต้นแล้ว แต่ในงานดังกล่าวไม่มีเหตุผลในเรื่องนี้ - ถ้าเราประกอบตัวกรองแล้วทำไมต้องวัดอย่างอื่นเราสามารถใช้มันตามที่เป็นอยู่ได้ นอกจากนี้ ค่าที่สำคัญที่สุดของตัวกรองดิจิทัลก็คือ ตัวกรองสามารถมีลักษณะเฉพาะที่ไม่สามารถบรรลุได้ (หรือบรรลุได้ยาก) ในความเป็นจริง เช่น เฟสเชิงเส้น ตรงนี้ไม่มีวิธีวัดเลย คุณแค่ต้องนับ
4. การได้รับการตอบสนองแบบแรงกระตุ้น
เมื่อมาถึงจุดนี้ ในสิ่งพิมพ์ส่วนใหญ่ในหัวข้อนี้ ผู้เขียนเริ่มทิ้งการแปลงรูป Z และเศษส่วนจากพหุนามจำนวนมากลงบนผู้อ่าน ทำให้เขาสับสนอย่างสิ้นเชิง ฉันจะไม่ทำเช่นนี้ ฉันจะอธิบายสั้น ๆ ว่าทั้งหมดนี้เกี่ยวกับอะไร และเหตุใดในทางปฏิบัติจึงไม่จำเป็นสำหรับสาธารณชนที่ก้าวหน้ามากนัก
สมมติว่าเราได้ตัดสินใจว่าเราต้องการอะไรจากตัวกรองและสร้างสมการที่อธิบายตัวกรองนั้น ถัดไป เพื่อค้นหาการตอบสนองแบบอิมพัลส์ คุณสามารถแทนที่ฟังก์ชันเดลต้าลงในสมการที่ได้รับแล้วได้ค่าที่ต้องการ ปัญหาเดียวคือต้องทำอย่างไร เนื่องจากฟังก์ชันเดลต้าตรงเวลา โอภูมิภาคนี้มอบให้โดยระบบอันชาญฉลาด และโดยทั่วไปแล้วจะมีอนันต์ทุกประเภท ดังนั้นในขั้นตอนนี้ทุกอย่างจึงกลายเป็นเรื่องยากลำบากมาก
นี่คือที่ที่พวกเขาจำได้ว่ามีสิ่งที่เรียกว่าการแปลงลาปลาซ โดยตัวมันเองมันไม่ใช่ลูกเกดหนึ่งปอนด์ เหตุผลเดียวที่ยอมรับได้ในวิศวกรรมวิทยุก็คือความจริงที่ว่าในพื้นที่ของการโต้แย้งว่าการเปลี่ยนแปลงนี้เป็นการเปลี่ยนแปลง บางสิ่งจะง่ายขึ้นจริงๆ โดยเฉพาะอย่างยิ่ง ฟังก์ชันเดลต้าแบบเดียวกันที่ทำให้เรามีปัญหาอย่างมากในโดเมนเวลานั้นสามารถแสดงออกมาได้อย่างง่ายดายมาก - มีเพียงฟังก์ชันเดียวเท่านั้น!
การแปลงรูป Z (หรือที่เรียกว่าการแปลงรูป Laurent) เป็นเวอร์ชันหนึ่งของการแปลงรูป Laplace สำหรับระบบแยก
นั่นคือโดยการใช้การแปลงลาปลาซ (หรือการแปลง Z ตามความจำเป็น) กับฟังก์ชันที่อธิบายตัวกรองที่ต้องการ โดยแทนที่ตัวกรองหนึ่งเป็นผลลัพธ์แล้วเปลี่ยนกลับ เราจะได้การตอบสนองแบบอิมพัลส์ ฟังดูง่ายใครๆ ก็ลองดูได้ ฉันจะไม่เสี่ยงเพราะดังที่ได้กล่าวไปแล้ว การแปลงลาปลาซเป็นสิ่งที่รุนแรง โดยเฉพาะอย่างยิ่งในทางกลับกัน ปล่อยให้เป็นทางเลือกสุดท้าย แล้วเราจะมองหาวิธีที่ง่ายกว่านี้เพื่อให้ได้สิ่งที่เรากำลังมองหา มีหลายคน
ประการแรก เราสามารถนึกถึงข้อเท็จจริงที่น่าทึ่งอีกประการหนึ่งของธรรมชาติได้ - คุณลักษณะของแอมพลิจูด-ความถี่และแรงกระตุ้นมีความสัมพันธ์ซึ่งกันและกันโดยการแปลงฟูริเยร์ที่ดีและคุ้นเคย ซึ่งหมายความว่าเราสามารถดึงการตอบสนองความถี่ใดๆ มาใช้กับรสนิยมของเรา นำการแปลงฟูริเยร์ผกผันจากนั้น (ไม่ว่าจะต่อเนื่องหรือแยกกัน) และรับการตอบสนองแบบอิมพัลส์ของระบบที่นำไปใช้ นี่มันน่าทึ่งมาก!
อย่างไรก็ตามเรื่องนี้จะไม่มีปัญหา ประการแรก การตอบสนองแบบกระตุ้นที่เราได้รับนั้นน่าจะไม่มีที่สิ้นสุด (ฉันจะไม่อธิบายว่าเหตุใด นั่นคือวิธีการทำงานของโลก) ดังนั้นเราจะต้องตัดสินใจโดยสมัครใจที่จะตัดมันทิ้งไป ณ จุดใดจุดหนึ่ง (การตั้งค่า มันเท่ากับศูนย์เลยจุดนั้น) แต่สิ่งนี้จะไม่เกิดขึ้นเช่นนั้น - ผลที่ตามมาจากสิ่งนี้อย่างที่คาดไว้คือการบิดเบือนการตอบสนองความถี่ของตัวกรองที่คำนวณได้ - มันจะกลายเป็นคลื่นและจุดตัดความถี่จะเบลอ
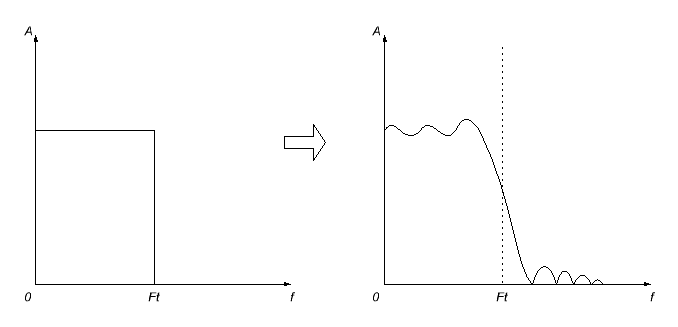
เพื่อลดผลกระทบเหล่านี้ ฟังก์ชันหน้าต่างการปรับให้เรียบต่างๆ จะถูกนำไปใช้กับการตอบสนองของอิมพัลส์ที่สั้นลง เป็นผลให้การตอบสนองความถี่มักจะเบลอมากยิ่งขึ้น แต่การสั่นที่ไม่พึงประสงค์ (โดยเฉพาะในพาสแบนด์) จะหายไป 
จริงๆ แล้ว หลังจากการประมวลผลดังกล่าว เราได้รับการตอบสนองแบบอิมพัลส์ที่ใช้งานได้ และสามารถสร้างตัวกรองดิจิทัลได้
วิธีการคำนวณที่สองนั้นง่ายกว่า - การตอบสนองแบบกระตุ้นของตัวกรองยอดนิยมนั้นแสดงออกมาในรูปแบบการวิเคราะห์มานานแล้วสำหรับเรา สิ่งที่เหลืออยู่คือการทดแทนค่าของคุณและใช้ฟังก์ชันหน้าต่างกับผลลัพธ์ตามที่คุณต้องการ คุณจึงไม่ต้องพิจารณาการแปลงใดๆ ด้วยซ้ำ
และแน่นอนว่า หากเป้าหมายคือการจำลองพฤติกรรมของวงจรใดวงจรหนึ่ง คุณสามารถรับการตอบสนองแบบอิมพัลส์ได้ในเครื่องจำลอง:
ที่นี่ฉันใช้พัลส์ 1,00500 โวลต์ (ใช่ 100.5 kV) ด้วยระยะเวลา 1 μs กับอินพุตของวงจร RC และได้รับการตอบสนองแบบอิมพัลส์ เป็นที่ชัดเจนว่าสิ่งนี้ไม่สามารถทำได้ในความเป็นจริง แต่ในเครื่องจำลองวิธีนี้อย่างที่คุณเห็นว่าใช้งานได้ดี
5. หมายเหตุ
สิ่งที่กล่าวไว้ข้างต้นเกี่ยวกับการลดการตอบสนองแรงกระตุ้นที่ใช้กับสิ่งที่เรียกว่าแน่นอน ตัวกรองการตอบสนองแรงกระตุ้นจำกัด (ตัวกรอง FIR/FIR) พวกมันมีคุณสมบัติที่มีคุณค่ามากมาย รวมถึงเฟสเชิงเส้น (ภายใต้เงื่อนไขบางประการสำหรับการสร้างการตอบสนองแบบอิมพัลส์) ซึ่งช่วยให้มั่นใจว่าไม่มีการบิดเบือนสัญญาณในระหว่างการกรอง รวมถึงความเสถียรที่สมบูรณ์ นอกจากนี้ยังมีตัวกรองการตอบสนองแบบอิมพัลส์ที่ไม่มีที่สิ้นสุด (ตัวกรอง IIR/IIR) มีการใช้ทรัพยากรน้อยกว่าในแง่ของการคำนวณ แต่ไม่มีข้อได้เปรียบที่ระบุไว้อีกต่อไป
ในบทความถัดไป ฉันหวังว่าจะดูตัวอย่างง่ายๆ ของการใช้งานตัวกรองดิจิทัลในทางปฏิบัติ
มหาวิทยาลัยเทคนิคแห่งรัฐโนโวซีบีร์สค์
คณะอัตโนมัติและวิศวกรรมคอมพิวเตอร์
กรมระบบรวบรวมและประมวลผลข้อมูล
วินัย "ทฤษฎีและการประมวลผลสัญญาณ"
งานห้องปฏิบัติการเลขที่10
ฟิลเตอร์ดิจิตอล
ด้วยลักษณะเฉพาะของแรงกระตุ้นอันจำกัด
กลุ่ม:เอที-33
ตัวเลือก: 1 ครู:
นักเรียน: Shadrina A.V. รศ. Shchetinin Yu.I.
เป้าหมายของงาน: ศึกษาวิธีการวิเคราะห์และการสังเคราะห์ตัวกรองการตอบสนองแบบไฟไนต์อิมพัลส์โดยใช้ฟังก์ชันหน้าต่างปรับให้เรียบ
เสร็จสิ้นการทำงาน:
1. แผนการตอบสนองแบบอิมพัลส์ของตัวกรอง FIR แบบ low-pass พร้อมความถี่ตัดหน้าต่างสี่เหลี่ยมสำหรับค่าความยาวตัวกรองและ
การตอบสนองแบบอิมพัลส์ของตัวกรอง FIR แบบแยกส่วนในอุดมคติมีความยาวไม่สิ้นสุดและไม่เป็นศูนย์สำหรับค่าลบของ :
.
เพื่อให้ได้ตัวกรองที่เป็นไปได้ทางกายภาพ ควรจำกัดการตอบสนองแบบอิมพัลส์ให้เป็นจำนวนจำกัด จากนั้นจึงเลื่อนการตอบสนองแบบตัดทอนไปทางขวาตามจำนวน
ค่าคือความยาว (ขนาด) ของตัวกรอง 
– ลำดับการกรอง
สคริปต์ Matlab (labrab101.m)
N = input("ป้อนความยาวตัวกรอง N = ");
h = บาป(wc.*(n-(N-1)/2))./(pi.*(n-(N-1)/2));
xlabel("หมายเลขอ้างอิง, n")
>> โครงเรื่องย่อย (2,1,1)
>> ลาบราบ101
ป้อนความยาวตัวกรอง N = 15
>> title("การตอบสนองแบบอิมพัลส์ของตัวกรอง FIR สำหรับ N=15")
>> โครงเรื่องย่อย (2,1,2)
>> ลาบราบ101
ป้อนความยาวตัวกรอง N = 50
>> title("การตอบสนองแบบอิมพัลส์ของตัวกรอง FIR สำหรับ N=50")
รูปที่ 1. แผนการตอบสนองแบบอิมพัลส์ของตัวกรอง FIR แบบ low-pass พร้อมความถี่ตัดหน้าต่างสี่เหลี่ยมสำหรับค่าความยาวตัวกรองและ
ความคิดเห็น:หากเราพิจารณาการตอบสนองความถี่ของตัวกรองดิจิทัลเป็นอนุกรมฟูเรียร์: 
จากนั้นค่าสัมประสิทธิ์ของซีรีย์นี้จะแสดงค่าของการตอบสนองแบบอิมพัลส์ของตัวกรอง ในกรณีนี้ อนุกรมฟูริเยร์ถูกตัดทอนในกรณีแรกเป็น และในกรณีที่สอง - ถึง จากนั้นคุณลักษณะที่ถูกตัดทอนจะถูกเลื่อนไปตามแกนตัวอย่างไปทางขวาเพื่อให้ได้ตัวกรองเชิงสาเหตุ เมื่อความกว้างของกลีบหลักคือ 2 และเมื่อ - 1 นั่นคือ เมื่อความยาวของตัวกรองเพิ่มขึ้น กลีบหลักของการตอบสนองแบบอิมพัลส์จะแคบลง หากเราพิจารณาระดับของกลีบด้านข้าง (โดยใช้ ) เมื่อเพิ่มขึ้นก็จะเพิ่มค่าสัมบูรณ์จาก เป็น . ดังนั้น เราสามารถสรุปได้ว่าเมื่อใช้การประมาณการตอบสนองความถี่ในอุดมคติของตัวกรองที่มีหน้าต่างสี่เหลี่ยม มันเป็นไปไม่ได้ที่จะจำกัดกลีบหลักให้แคบลงพร้อมกัน (และลดขอบเขตการเปลี่ยนแปลง) และลดระดับของกลีบด้านข้าง (ลด ระลอกคลื่นใน passband และ stopband ของตัวกรอง) พารามิเตอร์ที่ควบคุมได้เพียงอย่างเดียวของหน้าต่างสี่เหลี่ยมคือขนาดของมัน ซึ่งคุณสามารถกำหนดความกว้างของกลีบหลักได้ อย่างไรก็ตาม ไม่มีผลกระทบต่อกลีบด้านข้างมากนัก
2. การคำนวณ DVFT ของคุณลักษณะอิมพัลส์จากขั้นตอนที่ 1 โดยใช้ฟังก์ชัน กราฟการตอบสนองความถี่ในระดับเชิงเส้นและเป็นเดซิเบลสำหรับ 512 ตัวอย่างความถี่ Passband, แถบเปลี่ยนผ่าน และแถบหยุดของตัวกรอง อิทธิพลของลำดับตัวกรองต่อความกว้างของแถบการเปลี่ยนผ่านและระดับระลอกคลื่นตอบสนองความถี่ในแถบผ่านและหยุด
ฟังก์ชัน Matlab (DTFT.m)
ฟังก์ชัน = DTFT(x,M)
N = สูงสุด(M, ความยาว(x));
% ลด FFT เหลือขนาด 2^m
N = 2^(ceil(บันทึก(N)/log(2)));
% คำนวณ fft
% เวกเตอร์ความถี่
w = 2*pi*((0:(N-1))/N);
w = w - 2*pi*(w>=pi);
% Shift FFT เป็นช่วงจาก -pi ถึง +pi
X = fftshift(X);
w = fftshift(w);
สคริปต์ Matlab (labrab102.m)
h1 = บาป(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));
h2 = บาป(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));
DTFT(h1,512);
DTFT(h2,512);
พล็อต(w./(2*pi),abs(H1)./max(abs(H1)),,"r")
xlabel("f, Hz"), ylabel("|H1|/max(|H1|)"), ตาราง
พล็อต(w./(2*pi),abs(H2)./max(abs(H2)),,"b")
xlabel("f, Hz"), ylabel("|H2|/max(|H2|)"), ตาราง
พล็อต(w./(2*pi),20*log10(abs(H1)),,"r")
title("การตอบสนองความถี่ของตัวกรอง FIR แบบ low-pass พร้อมหน้าต่างสี่เหลี่ยมสำหรับ N = 15")
xlabel("f, Hz"), ylabel("20lg(|H1|), dB"), ตาราง
พล็อต(w./(2*pi),20*log10(abs(H2)),"b")
title("การตอบสนองความถี่ของตัวกรอง FIR แบบ low-pass พร้อมหน้าต่างสี่เหลี่ยมสำหรับ N = 50")
xlabel("f, Hz"), ylabel("20lg(|H2|), dB"), ตาราง
รูปที่ 2. แผนการตอบสนองความถี่ของตัวกรอง FIR แบบ low-pass พร้อมความถี่ตัดหน้าต่างสี่เหลี่ยมสำหรับค่าความยาวตัวกรองและในระดับเชิงเส้น
รูปที่ 3 แผนการตอบสนองความถี่ของตัวกรอง FIR แบบ low-pass พร้อมความถี่ตัดหน้าต่างสี่เหลี่ยมสำหรับค่าความยาวตัวกรองและในระดับลอการิทึม
ความคิดเห็น:
ตารางที่ 1. ช่วงของพาสแบนด์ ขอบเขตการเปลี่ยน และแถบหยุดสำหรับความยาวตัวกรองและ
|
ความยาวตัวกรอง |
แบนด์วิดท์, เฮิรตซ์ |
ภูมิภาคการเปลี่ยนผ่าน, Hz |
แถบหยุด, Hz |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
การบรรยายครั้งที่ 10 "ฟิลเตอร์ดิจิตอลที่มีการตอบสนองอิมพัลส์จำกัด" ฟังก์ชันถ่ายโอนของตัวกรองการตอบสนองอิมพัลส์จำกัดแบบดิจิทัลที่รับรู้ได้ทางกายภาพ (ตัวกรอง FIR) สามารถแสดงเป็นได้ (10.1). เมื่อแทนที่ในนิพจน์ (10.1) เราจะได้การตอบสนองความถี่ของตัวกรอง FIR ในรูปแบบ ที่ไหน เฟสล่าช้าตัวกรองถูกกำหนดให้เป็น ความล่าช้าของกลุ่มตัวกรองถูกกำหนดให้เป็น คุณลักษณะที่โดดเด่นของตัวกรอง FIR คือความสามารถในการใช้เฟสคงที่และความล่าช้าของกลุ่ม เช่น การตอบสนองเฟสเชิงเส้น (10.5), ที่ไหน - คงที่. หากตรงตามเงื่อนไขนี้ สัญญาณที่ผ่านตัวกรองจะไม่บิดเบือนรูปร่าง เพื่อให้ได้มาซึ่งเงื่อนไขที่รับประกันการตอบสนองเฟสเชิงเส้น เราเขียนการตอบสนองความถี่ของตัวกรอง FIR โดยคำนึงถึง (10.5) เราได้รับความเท่าเทียมระหว่างส่วนจริงและจินตภาพของความเท่าเทียมกันนี้ เราได้หารสมการที่สองด้วยสมการแรก ในที่สุดเราก็สามารถเขียนได้ สมการนี้มีสองคำตอบ ครั้งแรกเมื่อไรก =0 สอดคล้องกับสมการ สมการนี้มีคำตอบเฉพาะที่สอดคล้องกับข้อใดข้อหนึ่ง h (0) (sin (0)=0) และ h (n)=0 สำหรับ n >0. โซลูชันนี้สอดคล้องกับตัวกรองที่การตอบสนองแบบอิมพัลส์มีตัวอย่างที่ไม่เป็นศูนย์เพียงตัวเดียวในครั้งแรก ตัวกรองดังกล่าวไม่เป็นประโยชน์ในทางปฏิบัติ เราจะหาวิธีแก้ปัญหาอื่นสำหรับ. ในกรณีนี้ การคูณข้ามตัวเศษและส่วนใน (10.8) เราจะได้ (10.11). จากที่นี่เรามี เนื่องจากสมการนี้มีรูปแบบของอนุกรมฟูริเยร์ ดังนั้น คำตอบของสมการนี้ (หากมี) จึงไม่ซ้ำกัน จะเห็นได้ง่ายว่าการแก้สมการนี้ต้องเป็นไปตามเงื่อนไข (10.13), (10.14). จากเงื่อนไข (10.13) เป็นไปตามนั้นสำหรับลำดับตัวกรองแต่ละรายการเอ็น มีความล่าช้าเฟสเดียวเท่านั้นก ซึ่งสามารถบรรลุความเป็นเส้นตรงที่เข้มงวดของการตอบสนองเฟสได้ จากเงื่อนไข (10.14) เป็นไปตามว่าการตอบสนองอิมพัลส์ของตัวกรองจะต้องสมมาตรเกี่ยวกับจุดสำหรับคี่เอ็น และสัมพันธ์กับจุดกึ่งกลางของช่วงเวลา (รูปที่ 10.1)
การตอบสนองความถี่ของตัวกรองดังกล่าว (สำหรับคี่เอ็น ) สามารถเขียนได้ในรูป (10.15). ทำการทดแทนในจำนวนที่สองม. = N -1- n เราได้ (10.16). เนื่องจาก ชั่วโมง (n)= ชั่วโมง (N -1- n ) จากนั้นจึงนำผลรวมทั้งสองมารวมกันได้ แทนที่เราได้ (10.18). หากเรากำหนด ในที่สุดเราก็สามารถเขียนได้ ดังนั้นสำหรับตัวกรองที่มีการตอบสนองเฟสเชิงเส้นเรามี สำหรับกรณีคู่เอ็น เราจะมีเช่นเดียวกัน เราได้การทดแทนด้วยผลรวมที่สอง ทำการทดแทนเราได้รับ (10.24). กำหนดแล้ว ในที่สุดเราก็จะได้ ดังนั้นสำหรับตัวกรอง FIR ที่มีการตอบสนองเฟสเชิงเส้นและลำดับคู่ N สามารถเขียนได้ ต่อไปนี้ เพื่อความง่าย เราจะพิจารณาเฉพาะตัวกรองที่มีลำดับคี่เท่านั้น เมื่อทำการสังเคราะห์ฟังก์ชันถ่ายโอนตัวกรอง ตามกฎแล้วพารามิเตอร์เริ่มต้นจะเป็นข้อกำหนดสำหรับการตอบสนองความถี่ มีเทคนิคมากมายในการสังเคราะห์ตัวกรอง FIR ลองดูบางส่วนของพวกเขา เนื่องจากการตอบสนองความถี่ของตัวกรองดิจิทัลใดๆ เป็นฟังก์ชันคาบของความถี่ จึงสามารถแสดงเป็นอนุกรมฟูริเยร์ได้ โดยที่ค่าสัมประสิทธิ์ของอนุกรมฟูริเยร์เท่ากัน จะเห็นได้ว่าค่าสัมประสิทธิ์ของอนุกรมฟูริเยร์ชั่วโมง(น ) ตรงกับค่าสัมประสิทธิ์การตอบสนองแรงกระตุ้นของตัวกรอง ดังนั้นหากทราบคำอธิบายเชิงวิเคราะห์ของการตอบสนองความถี่ที่ต้องการของตัวกรองก็เป็นไปได้ที่จะกำหนดค่าสัมประสิทธิ์ของการตอบสนองแบบอิมพัลส์ได้อย่างง่ายดายและจากฟังก์ชันการถ่ายโอนของตัวกรอง อย่างไรก็ตาม ในทางปฏิบัติสิ่งนี้ไม่สามารถทำได้ เนื่องจากการตอบสนองแบบอิมพัลส์ของตัวกรองดังกล่าวมีความยาวไม่สิ้นสุด นอกจากนี้ ตัวกรองดังกล่าวไม่สามารถเกิดขึ้นได้ทางกายภาพเนื่องจากการตอบสนองแบบกระตุ้นเริ่มต้นที่ -¥ และไม่มีความล่าช้าอันจำกัดจะทำให้ตัวกรองนี้สามารถใช้งานได้จริง วิธีหนึ่งที่เป็นไปได้ในการได้รับตัวกรอง FIR ที่ประมาณการตอบสนองความถี่ที่กำหนดคือการตัดทอนอนุกรมฟูริเยร์ที่ไม่มีที่สิ้นสุดและการตอบสนองแบบอิมพัลส์ของตัวกรอง โดยสมมติว่าชั่วโมง (n)=0 ที่ . แล้ว ความสามารถในการรับรู้ทางกายภาพของฟังก์ชันการถ่ายโอนซ(ซ ) สามารถทำได้โดยการคูณ H(z) บน ที่ไหน (10.32). ด้วยการปรับเปลี่ยนฟังก์ชันถ่ายโอน ลักษณะแอมพลิจูดของตัวกรองจะไม่เปลี่ยนแปลง และความล่าช้าของกลุ่มจะเพิ่มขึ้นตามจำนวนคงที่ ตามตัวอย่าง ลองคำนวณตัวกรอง FIR ความถี่ต่ำผ่านที่มีการตอบสนองความถี่ของแบบฟอร์ม ตามข้อ (10.29) สัมประสิทธิ์การตอบสนองแรงกระตุ้นของตัวกรองอธิบายไว้ในนิพจน์ ตอนนี้จาก (10.31) เราสามารถรับนิพจน์สำหรับฟังก์ชันถ่ายโอนได้ ที่ไหน (10.36). ลักษณะแอมพลิจูดของตัวกรองที่คำนวณได้ต่างๆเอ็น แสดงในรูปที่ 10.2
รูปที่ 10.2 การกระเพื่อมในพาสแบนด์และสต็อปแบนด์เกิดขึ้นเนื่องจากการบรรจบกันอย่างช้าๆ ของอนุกรมฟูริเยร์ ซึ่งในทางกลับกัน ก็เกิดจากการที่ฟังก์ชันไม่ต่อเนื่องที่ความถี่คัตออฟของพาสแบนด์ การเต้นเป็นจังหวะเหล่านี้เรียกว่า ระลอกคลื่นกิ๊บส์. จากรูปที่ 10.2 จะเห็นได้ชัดเจนว่าเพิ่มขึ้นเอ็น ความถี่ของการเต้นเป็นจังหวะจะเพิ่มขึ้น และแอมพลิจูดจะลดลงทั้งที่ความถี่ต่ำและสูง อย่างไรก็ตาม แอมพลิจูดของระลอกสุดท้ายในพาสแบนด์และระลอกแรกในแถบหยุดยังคงไม่เปลี่ยนแปลงในทางปฏิบัติ ในทางปฏิบัติ ผลกระทบดังกล่าวมักไม่เป็นที่พึงปรารถนา ซึ่งต้องหาวิธีลดการเต้นเป็นจังหวะของกิ๊บส์ การตอบสนองแรงกระตุ้นที่ถูกตัดทอนชั่วโมง(น ) สามารถแสดงเป็นผลคูณของการตอบสนองแรงกระตุ้นอนันต์ที่ต้องการและบางส่วน ฟังก์ชั่นหน้าต่าง w (n) ความยาว n (รูปที่ 10.3)
ในกรณีที่พิจารณาถึงการตัดทอนอนุกรมฟูริเยร์อย่างง่าย เราจะใช้ หน้าต่างสี่เหลี่ยม ในกรณีนี้ การตอบสนองความถี่ของตัวกรองสามารถแสดงเป็นการบิดที่ซับซ้อนได้ ซึ่งหมายความว่าจะเป็นเวอร์ชัน "เบลอ" ของคุณลักษณะที่ต้องการ ปัญหาเกิดขึ้นที่การค้นหาฟังก์ชันหน้าต่างที่ทำให้สามารถลดการกระเพื่อมของ Gibbs ด้วยการเลือกตัวกรองแบบเดียวกัน เมื่อต้องการทำเช่นนี้ คุณต้องศึกษาคุณสมบัติของฟังก์ชันหน้าต่างโดยใช้ตัวอย่างของหน้าต่างสี่เหลี่ยมก่อน สเปกตรัมของฟังก์ชันหน้าต่างสี่เหลี่ยมสามารถเขียนได้เป็น สเปกตรัมของฟังก์ชันหน้าต่างสี่เหลี่ยมแสดงไว้ในรูปที่ 10.4
รูปที่ 10.4 เนื่องจาก ที่ ความกว้างของกลีบหลักของสเปกตรัมจะเท่ากับ การมีอยู่ของกลีบด้านข้างในสเปกตรัมของฟังก์ชันหน้าต่างทำให้การกระเพื่อมของ Gibbs เพิ่มขึ้นในการตอบสนองความถี่ของตัวกรอง เพื่อให้เกิดการกระเพื่อมต่ำในพาสแบนด์และการลดทอนสูงในแถบหยุด จำเป็นที่พื้นที่ที่ถูกจำกัดโดยกลีบด้านข้างจะเป็นเพียงส่วนเล็กๆ ของพื้นที่ที่ถูกจำกัดโดยกลีบหลัก ในทางกลับกัน ความกว้างของกลีบหลักจะกำหนดความกว้างของโซนการเปลี่ยนแปลงของตัวกรองผลลัพธ์ เพื่อให้สามารถเลือกตัวกรองได้สูง ความกว้างของกลีบหลักควรมีขนาดเล็กที่สุดเท่าที่จะเป็นไปได้ ดังที่เห็นจากด้านบน ความกว้างของกลีบหลักจะลดลงตามลำดับตัวกรองที่เพิ่มขึ้น ดังนั้นจึงสามารถกำหนดคุณสมบัติของฟังก์ชันหน้าต่างที่เหมาะสมได้ดังนี้ - ฟังก์ชั่นหน้าต่างต้องถูกจำกัดเวลา - สเปกตรัมของฟังก์ชันหน้าต่างควรใกล้เคียงกับฟังก์ชันที่จำกัดความถี่ได้ดีที่สุด เช่น มีพลังงานขั้นต่ำอยู่นอกกลีบหลัก - ความกว้างของกลีบหลักของสเปกตรัมฟังก์ชันหน้าต่างควรมีขนาดเล็กที่สุดเท่าที่จะเป็นไปได้ ฟังก์ชั่นหน้าต่างที่ใช้บ่อยที่สุดคือ: 1. หน้าต่างสี่เหลี่ยม. กล่าวถึงข้างต้น 2. ทุบหน้าต่าง ที่ไหน . หน้าต่างนี้เรียกว่าหน้าต่างฮันน์ (ฮันนิ่ง) 3. หน้าต่างแบล็คแมน 4. หน้าต่างของบาร์ตเลตต์ ตัวบ่งชี้ตัวกรองที่สร้างขึ้นโดยใช้ฟังก์ชันหน้าต่างที่ระบุสรุปไว้ในตาราง 10.1
ปัจจัยระลอกคลื่นถูกกำหนดให้เป็นอัตราส่วนของความกว้างสูงสุดของกลีบด้านข้างต่อความกว้างของกลีบหลักในสเปกตรัมของฟังก์ชันหน้าต่าง ในการเลือกลำดับตัวกรองที่ต้องการและฟังก์ชันหน้าต่างที่เหมาะสมที่สุดเมื่อคำนวณตัวกรองจริง คุณสามารถใช้ข้อมูลในตาราง 10.2
ดังที่เห็นได้จากตาราง 10.1 มีความสัมพันธ์บางอย่างระหว่างค่าสัมประสิทธิ์การกระเพื่อมและความกว้างของกลีบหลักในสเปกตรัมของฟังก์ชันหน้าต่าง ยิ่งค่าสัมประสิทธิ์การเต้นของชีพจรน้อยลง ความกว้างของกลีบหลักก็จะมากขึ้น และโซนการเปลี่ยนแปลงในการตอบสนองความถี่ของตัวกรองก็จะมากขึ้นด้วย เพื่อให้แน่ใจว่ามีการกระเพื่อมต่ำในพาสแบนด์ จำเป็นต้องเลือกหน้าต่างที่มีค่าสัมประสิทธิ์การกระเพื่อมที่เหมาะสม และจัดเตรียมความกว้างที่ต้องการของโซนการเปลี่ยนแปลงด้วยลำดับตัวกรองที่เพิ่มขึ้น N ปัญหานี้สามารถแก้ไขได้โดยใช้หน้าต่างที่ Kaiser เสนอ ฟังก์ชันหน้าต่าง Kaiser มีรูปแบบ
โดยที่ a เป็นพารามิเตอร์อิสระ
คุณสมบัติที่น่าสนใจของหน้าต่าง Kaiser คือความสามารถในการเปลี่ยนค่าสัมประสิทธิ์การเต้นของจังหวะจากค่าเล็กไปเป็นค่าขนาดใหญ่ได้อย่างราบรื่นในขณะที่เปลี่ยนพารามิเตอร์ a เพียงตัวเดียว ในกรณีนี้ สำหรับฟังก์ชันหน้าต่างอื่นๆ ความกว้างของกลีบหลักสามารถปรับได้ตามลำดับตัวกรอง N พารามิเตอร์หลักที่กำหนดเมื่อพัฒนาตัวกรองจริงคือ: แบนด์วิธ - wp ; แถบอุปสรรค - w a ; ระลอกคลื่นสูงสุดที่อนุญาตในพาสแบนด์คือ A p ; การลดทอนแถบหยุดขั้นต่ำ – A a ; -ความถี่ในการสุ่มตัวอย่าง -ส. พารามิเตอร์เหล่านี้แสดงไว้ในรูปที่ 10.5 ในกรณีนี้ ระลอกสูงสุดในพาสแบนด์จะถูกกำหนดเป็น
และการลดทอนขั้นต่ำในแถบหยุดจะเป็นดังนี้ ขั้นตอนที่ค่อนข้างง่ายในการคำนวณตัวกรองด้วยหน้าต่าง Kaiser มีขั้นตอนต่อไปนี้: 1. พิจารณาการตอบสนองแบบอิมพัลส์ของตัวกรอง h (n) โดยมีเงื่อนไขว่าการตอบสนองความถี่เหมาะสมที่สุด
โดยที่ (10.49) 2. เลือกพารามิเตอร์ d เป็น
ที่ไหน 3. ค่าที่แท้จริงของ A a และ A p คำนวณโดยใช้สูตร (10.46), (10.47) 4.พารามิเตอร์ a ถูกเลือกเป็น
5.พารามิเตอร์ D ถูกเลือกเป็น
6. เลือกค่าคี่ที่น้อยที่สุดของลำดับตัวกรองจากเงื่อนไข
ตามนั้น เนื่องจากตัวอย่างของการตอบสนองอิมพัลส์ของตัวกรองคือค่าสัมประสิทธิ์ของฟังก์ชันการถ่ายโอน เงื่อนไข (10.59) หมายความว่ารหัสของค่าสัมประสิทธิ์ตัวกรองทั้งหมดมีเพียงส่วนเศษส่วนและบิตเครื่องหมายเท่านั้น และไม่มีส่วนจำนวนเต็ม จำนวนหลักของส่วนเศษส่วนของค่าสัมประสิทธิ์ตัวกรองถูกกำหนดจากเงื่อนไขของการตอบสนองฟังก์ชันการถ่ายโอนตัวกรองด้วยค่าสัมประสิทธิ์เชิงปริมาณซึ่งเป็นข้อกำหนดที่ระบุสำหรับการเข้าใกล้ฟังก์ชันการถ่ายโอนอ้างอิงด้วยค่าสัมประสิทธิ์ที่แน่นอน ค่าสัมบูรณ์ของตัวอย่างสัญญาณอินพุตตัวกรองมักจะถูกทำให้เป็นมาตรฐานเช่นนั้น หากทำการวิเคราะห์สำหรับตัวกรอง FIR ที่มีการตอบสนองเฟสเชิงเส้นอัลกอริทึมสำหรับการคำนวณสัญญาณเอาท์พุตอาจเป็นดังนี้ โดยที่ค่าสัมประสิทธิ์ตัวกรองถูกปัดเศษเป็น sk อัลกอริทึมนี้สอดคล้องกับแผนภาพบล็อกตัวกรองที่แสดงในรูปที่ 10.5
มีสองวิธีในการใช้อัลกอริทึมนี้ ในกรณีแรก การดำเนินการคูณทั้งหมดจะดำเนินการทุกประการและไม่มีการปัดเศษผลคูณ ในกรณีนี้ ความลึกบิตของผลิตภัณฑ์จะเท่ากับ s ใน +s k โดยที่ s in คือความลึกบิตของสัญญาณอินพุต และ sk คือความลึกบิตของสัมประสิทธิ์ตัวกรอง ในกรณีนี้ บล็อกไดอะแกรมของตัวกรองที่แสดงในรูปที่ 10.5 สอดคล้องกับตัวกรองจริงทุกประการ ในวิธีที่สองของการใช้อัลกอริทึม (10.61) แต่ละผลลัพธ์ของการดำเนินการคูณจะถูกปัดเศษ นั่นคือ สินค้าถูกคำนวณโดยมีข้อผิดพลาดบางประการ ในกรณีนี้จำเป็นต้องเปลี่ยนอัลกอริธึม (10.61) เพื่อคำนึงถึงข้อผิดพลาดที่เกิดจากการปัดเศษผลิตภัณฑ์ หากค่าตัวอย่างของสัญญาณเอาต์พุตตัวกรองคำนวณโดยใช้วิธีแรก (ด้วยค่าที่แน่นอนของผลิตภัณฑ์) การกระจายตัวของสัญญาณรบกวนเอาต์พุตจะถูกกำหนดเป็น
เหล่านั้น. ขึ้นอยู่กับความแปรปรวนของสัญญาณรบกวนการปัดเศษของสัญญาณอินพุตและค่าของค่าสัมประสิทธิ์ตัวกรอง จากที่นี่คุณจะพบจำนวนบิตที่ต้องการของสัญญาณอินพุตเป็น
การใช้ค่าที่ทราบของ s in และ sk เราสามารถกำหนดจำนวนบิตที่จำเป็นสำหรับส่วนที่เป็นเศษส่วนของรหัสสัญญาณเอาท์พุตได้ดังนี้ หากค่าของตัวอย่างสัญญาณเอาท์พุตคำนวณโดยใช้วิธีที่สองเมื่อแต่ละผลิตภัณฑ์ถูกปัดเศษเป็นตัวเลข d การกระจายตัวของสัญญาณรบกวนการปัดเศษที่สร้างขึ้นโดยตัวคูณแต่ละตัวสามารถแสดงในรูปของความจุหลักของ สินค้าเป็น DR เข้าและอัตราส่วนสัญญาณต่อเสียงรบกวนที่เอาต์พุตตัวกรอง SNR ออก ช่วงไดนามิกของสัญญาณอินพุตในหน่วยเดซิเบลถูกกำหนดเป็น
โดยที่ค่าสูงสุดและค่าต่ำสุดคือแอมพลิจูดสูงสุดและต่ำสุดของสัญญาณอินพุตตัวกรอง อัตราส่วนสัญญาณต่อเสียงรบกวนที่เอาต์พุตตัวกรอง ซึ่งแสดงเป็นเดซิเบล ถูกกำหนดเป็น
กำหนดค่ารากกำลังสองเฉลี่ยของกำลังของสัญญาณไซน์ซอยด์เอาต์พุตของตัวกรองด้วยแอมพลิจูด A min และ (10.77) กำหนดกำลังเสียงที่เอาต์พุตตัวกรอง จาก (10.75) และ (10.76) ด้วย A max =1 เราได้รับนิพจน์สำหรับการกระจายตัวของสัญญาณรบกวนเอาต์พุตของตัวกรอง ค่าการกระจายสัญญาณรบกวนเอาต์พุตของตัวกรองนี้สามารถใช้เพื่อคำนวณความลึกบิตของสัญญาณอินพุตและเอาต์พุตของตัวกรอง  โลกแห่งโปรแกรมฟรีและเคล็ดลับที่เป็นประโยชน์ 2024 whatsappss.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(10.2),
- การตอบสนองความถี่แอมพลิจูด (AFC)กรอง,
- การตอบสนองความถี่เฟส (PFC)กรอง.
(10.3).
(10.4).
(10.6).
(10.7).
(10.8).
(10.9).
(10.10).
(10.12).
(10.17).
(10.19),
(10.20).
(10.21).
(10.22).
(10.23).
(10.25),
(10.26).
(10.27).
(10.28),
(10.29).
(10.30).
(10.31),
(10.33).
(10.34).
(10.35),
(10.37).
(10.38).
(10.39).
(10.40).
(10.41),
(10.42).
(10.43).
(10.44),
, I 0 – ฟังก์ชัน Bessel ของลำดับศูนย์ชนิดแรก ซึ่งกำหนดโดยนิพจน์
(10.45).
(10.46),
(10.50),
(10.51).
(10.52).
(10.53).
(10.54),
(10.57)
(10.66),
(10.67).
(10.74),
(10.75),
(10.78).