Impulzni odziv filtra. Digitalni filtri s končnim impulznim odzivom. Glajenje podatkov. Srednje filtriranje
48 Digitalni filtri s končnim impulznim odzivom. Izračun kih filtrov.
Filter s končnim impulznim odzivom (Nerekurzivni filter, FIR filter) ali FIR filter (FIR je okrajšava od končni impulzni odziv - končni impulzni odziv) - ena od vrst linearnih digitalnih filtrov, katerih značilnost je časovna omejitev impulzni odziv(od neke točke v času postane natanko enak nič). Tak filter zaradi pomanjkanja povratne informacije imenujemo tudi nerekurziven. Imenovalec prenosne funkcije takega filtra je določena konstanta.
Diferenčna enačba, ki opisuje razmerje med vhodnimi in izhodnimi signali filtra: kjer p- vrstni red filtrov, x(n) - vhodni signal, l(n) je izhodni signal in b jaz- koeficienti filtra. Z drugimi besedami, vrednost katerega koli vzorca izhodnega signala je določena z vsoto skaliranih vrednosti p prejšnja branja. Lahko rečemo drugače: vrednost izhoda filtra v katerem koli trenutku je vrednost odziva na trenutno vrednost vhoda in vsota vseh postopoma upadajočih odzivov p prejšnji vzorci signala, ki še vedno vplivajo na izhod (po p-šteje, postane prehodna funkcija impulza enaka nič, kot je bilo že omenjeno, torej vsi členi za p-th bo prav tako postalo enako nič). Zapišimo prejšnjo enačbo v bolj zmogljivi obliki:
Če želite najti jedro filtra, ki smo ga postavili
x(n) = δ( n)
kjer je δ( n) - delta funkcija. Potem lahko impulzni odziv FIR filtra zapišemo kot:
Z-transformacija impulznega odziva nam da prenosno funkcijo filtra FIR:
]Lastnosti
Filter FIR ima številne uporabne lastnosti, zaradi katerih je včasih bolje uporabiti kot filter IIR. Tukaj je nekaj izmed njih:
FIR filtri so robustni.
Filtri FIR ne potrebujejo povratne informacije, ko so implementirani.
Fazo FIR filtrov lahko naredimo linearno
Neposredna oblika FIR filtra
FIR filtre je mogoče implementirati z uporabo treh elementov: množitelja, seštevalnika in bloka zakasnitve. Možnost, prikazana na sliki, je neposredna izvedba FIR filtrov tipa 1.
Izvedba direktne oblike FIR filtra
Primer programa
Spodaj je primer FIR filtrskega programa, napisanega v C:
/* FIR filter za 128 pip */
float fir_filter (plavajoči vnos)
statični plovni vzorec;
acc = 0,0f; /* Baterija */
/* Množi in kopiči */
za (i = 0; i< 128; i++) {
acc += (h[i] * vzorec[i]);
/* Izhod */
/* Premakni zakasnjeni signal */
za (i = 127; i > 0; i--)
vzorec [i] = vzorec;
49 Glajenje podatkov. Drseče povprečje.
50 Glajenje podatkov. Parabolično glajenje.
51 Glajenje podatkov. Spencerjevo glajenje.
52 Glajenje podatkov. Srednje filtriranje.
Drseče povprečje, parabolično glajenje, Spencerjevo glajenje, mediansko filtriranje
Pri razvoju metod za določanje parametrov fizičnih procesov, ki se skozi čas počasi spreminjajo, je pomembna naloga odpraviti vpliv šumnih učinkov ali naključnih motenj, ki se prekrivajo z obdelanim signalom, prejetim na izhodu primarnega pretvornika.
Če želite odpraviti ta učinek, lahko uporabite glajenje podatkov. Eden najpreprostejših načinov takšnega glajenja je aritmetično povprečje. Pri uporabi se vsaka vrednost diskretne funkcije (matrika obdelanih podatkov) izračuna v skladu z izrazom:
kjer je število točk za aritmetično povprečje (liho celo število);
Vrednost funkcije pred obdelavo;
Obstajajo tudi druge precej učinkovite metode glajenja, na primer s parabolami druge stopnje na petih, sedmih, devetih in enajstih točkah v skladu z izrazi:
ali parabole četrte stopnje na sedmih, devetih, enajstih in trinajstih točkah:
V praktičnih aplikacijah druge učinkovite metode, na primer 15-točkovno Spencerjevo glajenje, dajejo dobre rezultate:
Z zamenjavo kompleksne eksponente , kjer v te izraze, lahko določimo prenosno funkcijo ustrezne transformacije.
Za aritmetično povprečje
Izraz v oklepaju predstavlja geometrijsko napredovanje z imenovalcem, zato lahko ta izraz predstavimo kot:
.
Ta formula predstavlja karakteristiko prenosa nizkopasovnega filtra in kaže, da več kot je členov vključenih v povprečenje, večja je potlačitev visokofrekvenčnih šumnih komponent v signalu (glej sliko 6.1).
Vendar se semantični koncept frekvence pri obdelavi časovnih trendov razlikuje od podobnega koncepta pri obdelavi signalov. To je razloženo z dejstvom, da pri preučevanju časovnih trendov ni zanimiva njihova frekvenčna sestava, temveč vrsta spremembe (povečanje, zmanjšanje, konstantnost, cikličnost itd.).
Za glajenje podatkov je zelo učinkovita tudi uporaba tako imenovanih hevrističnih algoritmov.
Eden od njih je mediansko filtriranje. Med izvajanjem v drsečem časovnem oknu dimenzije , kjer je celo število liho število, se osrednji element nadomesti s srednjim elementom zaporedja, ki so v naraščajočem vrstnem redu vrednosti razvrščeni elementi podatkovnega niza zglajenega signal, ki spada v časovno okno. Prednost medianega filtriranja je zmožnost odstranjevanja impulznega šuma, katerega trajanje ne presega, skoraj brez popačenja gladko spremenljivih signalov. Ta metoda zatiranja hrupa nima stroge matematične utemeljitve, vendar sta preprostost izračunov in učinkovitost dobljenih rezultatov privedli do njegove široke uporabe.
Slika 6.1 - Grafi prenosnih karakteristik
aritmetične operacije povprečenja za m=5, 7, 9, 11
Drug zanimiv algoritem za glajenje je povprečje mediane. Njegovo bistvo je naslednje. V drsečem časovnem oknu velikosti (-liho celo število) so elementi podatkovne matrike razvrščeni v naraščajočem vrstnem redu, nato pa sta prvi in zadnji element odstranjena iz urejenega zaporedja (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
Ta metoda vam omogoča zatiranje pulznih in radiofrekvenčnih motenj ter doseganje dobrega glajenja signala.
| " |
Razmislimo o najpreprostejših digitalnih filtrih - filtrih s konstantnimi parametri.
Vhodni signal digitalnega filtra je dobavljen v obliki zaporedja številskih vrednosti, ki si sledijo v intervalih (slika 4.1, a). Ko digitalni filter prejme vsako naslednjo vrednost signala, se izračuna naslednja vrednost izhodnega signala.Algoritmi za izračun so lahko zelo različni; med postopkom izračuna, poleg zadnje vrednosti vhodnega signala, lahko uporabite
prejšnje vrednosti vhodnih in izhodnih signalov: Izhodni signal digitalnega filtra je tudi zaporedje numeričnih vrednosti, ki sledijo intervalu . Ta interval je enak za celotno napravo za digitalno obdelavo signalov.
riž. 4.1. Signal na vhodu in izhodu digitalnega filtra
Torej, če na vhod digitalnega filtra uporabite najpreprostejši signal v obliki enega samega impulza (slika 4.2, a)
potem na izhodu dobimo signal v obliki diskretnega zaporedja številskih vrednosti, ki si sledijo v intervalih
Po analogiji z običajnimi analognimi vezji bomo ta odzivni signal imenovali impulzni odziv filtra (slika 4.2, b). Za razliko od impulznega odziva analognega vezja je funkcija brezdimenzijska.
riž. 4.2. Enotni impulz in impulzni odziv digitalnega filtra
Uporabimo poljuben diskretni signal na vhod filtra (sl. 4.1, a), ki je niz diskretnih vrednosti
Pod delovanjem prvega elementa se na izhodu filtra oblikuje zaporedje, pomnoženo s, pod delovanjem se zaporedje pomnoži z in premakne v desno za količino itd. Posledično bo izhod dobil zaporedje kje
Tako je izhodni signal definiran kot diskretna konvolucija vhodnega signala in impulznega odziva. V tem pogledu so digitalni filtri podobni običajnim vezjem, kjer je izhodni signal enak konvoluciji vhodnega signala in impulznega odziva.
Formula (4.1) je algoritem digitalnega filtriranja. Če je impulzni odziv filtra opisan z zaporedjem s končnim številom členov, potem je filter mogoče izvesti v obliki vezja, prikazanega na sl. 4.3. Tukaj črka označuje elemente zakasnitve signala za čas (na celico); -elementi, ki pomnožijo signal z ustreznim koeficientom.
Diagram, prikazan na sl. 4.3 ni električni tokokrog digitalnega filtra; Ta diagram je grafična predstavitev algoritma digitalnega filtriranja in prikazuje zaporedje aritmetičnih operacij, izvedenih med obdelavo signala.
riž. 4.3. Nerekurzivno digitalno filtrsko vezje
Za digitalne filtre, ki obdelujejo signale v obliki abstraktnih numeričnih zaporedij, koncept "časovne zakasnitve" ni povsem pravilen. Zato so elementi, ki zakasnijo signal za eno celico, običajno označeni na vezjih digitalnih filtrov s simbolom, ki označuje zakasnitev signala v jeziku -transformacij. V nadaljevanju se bomo tega zapisa držali.
Vrnimo se k vezju digitalnega filtra, prikazanemu na sl. 4.3 Takšni filtri, kjer se za izračun uporabljajo samo vrednosti vhodnega signala, se imenujejo preprosti ali nerekurzivni.
Algoritem nerekurzivnega filtra je enostavno napisati, če je impulzni odziv filtra znan. Za praktično izvedbo algoritma je potrebno, da impulzni odziv vsebuje končno število členov. Če impulzni odziv vsebuje neskončno število pogojev, vendar se njihova vrednost hitro zmanjša, se lahko omejite na končno število izrazov in zavržete tiste, katerih vrednosti so majhne. Če se vrednost elementov impulznega odziva ne zmanjša, se algoritem nerekurzivnega filtra izkaže za neuresničljivega.
riž. 4.4. - veriga
Kot primer razmislite o najpreprostejšem digitalnem filtru, podobnem -vezju (slika 4.4). Impulzni odziv vezja ima obliko
Za zapis impulznega odziva ustreznega digitalnega filtra je treba izraz nadomestiti z Vendar pa ima impulzni odziv vezja dimenzijo in mora biti impulzni odziv digitalnega filtra brezdimenzijsko. Zato v izrazu (4.2) izpustimo množitelj in zapišemo impulzni odziv digitalnega filtra v obliki
Takšen impulzni odziv vsebuje neskončno veliko členov, vendar njihova velikost pada po eksponentnem zakonu in se lahko omejimo na člene, pri čemer izberemo tako, da
Zdaj lahko zapišemo izraz za signal na izhodu filtra
Ta izraz je tudi algoritem digitalnega filtra. Diagram tega filtra je prikazan na sl. 4.5.
Drugi pristop k analizi procesov v digitalnih filtrih je podoben operaterski metodi analize običajnih analognih vezij, le da se namesto Laplaceove transformacije uporablja -transformacija.
riž. 4.5. Vezje nerekurzivnega digitalnega filtra, podobno -vezju
Določimo parameter digitalnega filtra, podoben prenosni funkciji električnega vezja. Če želite to narediti, uporabite transformacijo za impulzni odziv digitalnega filtra:
Funkcija se imenuje funkcija sistemskega filtra.
V skladu z izrazom (4.1) je signal na izhodu digitalnega filtra enak diskretni konvoluciji vhodnega signala in impulznega odziva filtra. Če za ta izraz uporabimo konvolucijski izrek, dobimo, da je transformacija izhodnega signala enaka transformaciji vhodnega signala, pomnoženi s funkcijo sistemskega filtra:
Tako sistemska funkcija igra vlogo prenosne funkcije digitalnega filtra.
Kot primer poiščimo sistemsko funkcijo digitalnega filtra prvega reda, podobnega -vezju:
Tretja metoda analize prehoda signalov skozi digitalne filtre je podobna klasični metodi diferencialnih enačb. Oglejmo si to metodo na primeru verig naročil.
Najenostavnejše analogno vezje 1. reda je -vezje (glej sliko 4.4), prehod signalov skozi katerega opisuje diferencialna enačba
Za diskretno vezje je treba namesto diferencialne enačbe (4.8) zapisati diferencialno enačbo, kjer sta vhodni in izhodni signal podana za diskretne časovne trenutke, namesto odvoda pa razlika sosednjih vrednosti signala. pojavijo. Za diskretno vezje 1. reda lahko diferenčno enačbo zapišemo v precej splošni obliki
Uporabimo transformacijo za enačbo
kjer najdemo funkcijo sistemskega filtra
Formula (4.10) je precej splošen izraz za sistemsko funkcijo digitalnega filtra 1. reda. Ko sovpada s predhodno dobljenim izrazom (4.7) za sistemsko funkcijo digitalnega filtra, ki je enakovreden -vezju.
Poiščimo algoritem digitalnega filtriranja, ki ustreza sistemski funkciji (4.10). Da bi to naredili, rešimo enačbo (4.9) za
Enakovreden diagram tega algoritma je prikazan na sl. 4.6. V primerjavi z nerekurzivnim filtrom (glej sliko 4.5) je tukaj dodana vrsta "povratnega vezja", kar pomeni, da se vrednosti izhodnega signala uporabijo v naslednjih
riž. 4.6. Vezje rekurzivnega digitalnega filtra, podobno -vezju
izračuni. Filtri te vrste se imenujejo rekurzivni.
Algoritem (4.11) ustreza filtru, ki je popolnoma enakovreden prej obravnavanemu nerekurzivnemu filtru. Toda za določitev ene vrednosti izhodnega signala z algoritmom nerekurzivnega filtra (4.4) je potrebno izvesti operacije, pri uporabi algoritma rekurzivnega filtra (4.11) pa sta potrebni le dve operaciji. To je glavna prednost rekurzivnih filtrov. Poleg tega rekurzivni filtri omogočajo obdelavo signala z večjo natančnostjo, saj omogočajo pravilnejšo izvedbo impulznega odziva brez zavrženja njegovega "repa". Rekurzivni filtri vam omogočajo implementacijo algoritmov, ki jih z nerekurzivnimi filtri sploh ni mogoče implementirati. Na primer, s filtrom, ki deluje v skladu z vezjem na sl. 4.6, je v bistvu idealen akumulator-integrator in ima impulzni odziv oblike. Filtra s takšno karakteristiko ni mogoče izvesti z uporabo nerekurzivne sheme.
Obravnavani primeri kažejo, da za ustvarjanje digitalnih filtrov z dolgim impulznim odzivom nima smisla uporabljati nerekurzivnih algoritmov. V teh primerih je bolj primerna uporaba rekurzivnih filtrov.
Področje uporabe nerekurzivnih algoritmov je izvedba digitalnih filtrov z impulznim odzivom, ki vsebuje majhno število členov. Primer je najpreprostejši diferenciator, katerega izhodni signal je enak prirastku vhodnega signala:
Vezje takšnega digitalnega filtra je prikazano na sl. 4.7.
riž. 4.7. Vezje najpreprostejšega digitalnega diferenciatorja
Oglejmo si zdaj splošni digitalni filter, ki ga opisuje enačba
To enačbo lahko obravnavamo kot diferenčno enačbo reda in kot algoritem digitalnega filtriranja, če jo prepišemo drugače, namreč
riž. 4.8. Vezje filtra rekurzivnega digitalnega reda
Algoritem (4.13) ustreza vezju, prikazanemu na sl. 4.8. Poiščimo sistemsko funkcijo takega filtra. Če želite to narediti, uporabite transformacijo za enačbo:
Izraz (4.14) nam omogoča vzpostavitev povezave med nihanji elementov filtrskega kroga in funkcijo sistema. Koeficienti v števcu sistemske funkcije določajo vrednosti koeficientov za
(v nerekurzivnem delu filtra), koeficienti v imenovalcu pa določajo rekurzivni del filtra.
Vse se je začelo, ko je prijatelj prijatelja potreboval pomoč s temi istimi filtri. Po jedijskih poteh so govorice o tem prišle do mene, odjavil sem se v komentarjih na objavo na povezavi. Zdelo se je, da pomaga. No, upam.
Ta zgodba mi je obudila spomine na tretji ali nekaj podobnega tečaju, ko sem sam opravljal DSP, in me spodbudila, da napišem članek za vse tiste, ki jih zanima delovanje digitalnih filtrov, a jih je seveda strah pred -najboljše formule in psihedelične risbe v (že ne govorim o učbenikih).
Na splošno po mojih izkušnjah stanje z učbeniki opisuje znana fraza, da včasih za drevesi ne vidiš gozda. In ko te začnejo takoj strašiti z Z-transformacijo in formulami za deljenje polinomov, ki so pogosto daljši od dveh plošč, zanimanje za temo zelo hitro usahne. Začeli bomo s preprostim; na srečo, da bi razumeli, kaj se dogaja, sploh ni potrebno opisovati dolgih zapletenih izrazov.
Torej, najprej nekaj preprostih osnovnih pojmov.
1. Impulzni odziv.
Recimo, da imamo škatlo s štirimi zatiči. Nimamo pojma, kaj je notri, vendar zagotovo vemo, da sta leva terminala vhod, desna pa izhod. Poskusimo nanj uporabiti zelo kratek impulz zelo velike amplitude in poglejmo, kaj se zgodi na izhodu. No, ni jasno, kaj je znotraj tega kvadripola, ker ni jasno, kako ga opisati, a bomo vsaj videli nekaj.
Pri tem je treba povedati, da se kratek (na splošno neskončno kratek) impulz velike (na splošno neskončne) amplitude v teoriji imenuje delta funkcija. Mimogrede, smešno je, da je integral tega neskončno funkcija je enaka ena. To je normalizacija.
Torej, kar smo videli na izhodu kvadripolnega omrežja, potem ko smo uporabili delta funkcijo za vhod, se imenuje impulzni odziv ta kvadripol. Zaenkrat sicer ni jasno, kako nam bo pomagal, a spomnimo se le dobljenega rezultata in pojdimo k naslednjemu zanimivemu konceptu.
2. Konvolucija.
Na kratko, konvolucija je matematična operacija, ki se zmanjša na integracijo produkta funkcij:
Kot lahko vidite, je označen z zvezdico. Vidite lahko tudi, da se med konvolucijo ena funkcija prevzame v svojem vrstnem redu "naprej", skozi drugo pa gremo "zadaj naprej". Seveda gre v diskretnem primeru, ki je za človeštvo bolj dragocen, konvolucija, tako kot vsak integral, v seštevek:
Zdelo bi se kot nekakšna dolgočasna matematična abstrakcija. Vendar je v resnici snop morda najbolj čaroben pojav tega sveta, po neverjetnosti je takoj za rojstvom človeka, s to razliko, da večina ljudi vsaj do leta starosti izve, od kod prihajajo otroci. osemnajst, medtem ko o tem, kaj je konvolucija in zakaj je uporabna in neverjetna, ogromen del zemeljske populacije vse življenje nima prav nič pojma.
Moč te operacije je torej v tem, da če je f poljuben vhodni signal in je g impulzni odziv štiriportnega omrežja, bo rezultat konvolucije teh dveh funkcij podoben tistemu, kar bi dobite s prenosom signala f skozi to omrežje s štirimi vrati.
To pomeni, da je impulzni odziv popolna kombinacija vseh lastnosti štiriportnega omrežja glede na vhodni učinek, konvolucija vhodnega signala z njim pa vam omogoča obnovitev ustreznega izhodnega signala. Po mojem mnenju je to preprosto neverjetno!
3. Filtri.
Z impulznim odzivom in konvolucijo lahko naredite veliko zanimivih stvari. Na primer, če je signal zvok, lahko organizirate reverb, echo, chorus, flanger in še veliko, veliko več; lahko razlikujete in integrirate ... Na splošno lahko ustvarite karkoli. Za nas je zdaj najbolj pomembno, da seveda filtre enostavno dobimo tudi s konvolucijo.
Sam digitalni filter je konvolucija vhodnega signala z impulznim odzivom, ki ustreza želenemu filtru.
Seveda je treba impulzni odziv nekako doseči. Seveda smo že ugotovili, kako ga izmeriti zgoraj, vendar je pri taki nalogi malo smisla - če smo filter že sestavili, zakaj bi merili karkoli drugega, lahko ga uporabimo, kot je. In poleg tega je najpomembnejša vrednost digitalnih filtrov ta, da imajo lahko lastnosti, ki so v resnici nedosegljive (ali zelo težko dosegljive) - na primer linearna faza. Tukaj torej sploh ni mogoče meriti, samo šteti je treba.
4. Pridobivanje impulznega odziva.
Na tej točki v večini publikacij na to temo začnejo avtorji bralca zlagati gore Z-transformacij in ulomkov iz polinomov in ga popolnoma zmedejo. Tega ne bom, le na kratko bom razložil, za kaj gre in zakaj v praksi napredni javnosti to ni preveč potrebno.
Recimo, da smo se odločili, kaj želimo od filtra, in ustvarili enačbo, ki ga opisuje. Nato lahko za iskanje impulznega odziva nadomestite delta funkcijo v izpeljano enačbo in dobite želeno. Edina težava je, kako to narediti, ker je delta funkcija v času O regija je podana z zvitim sistemom in na splošno obstajajo vse vrste neskončnosti. Tako se na tej stopnji vse izkaže za strašno težko.
Tu se zgodi, da se spomnijo, da obstaja nekaj takega, kot je Laplaceova transformacija. Sama po sebi ni funt rozin. Edini razlog, da je v radiotehniki toleriran, je ravno dejstvo, da se v prostoru argumenta, v katerega je ta transformacija prehod, nekatere stvari dejansko poenostavijo. Zlasti ista delta funkcija, ki nam je povzročala toliko težav v časovni domeni, je zelo enostavno izražena - tam je samo ena!
Z-transformacija (tudi Laurentova transformacija) je različica Laplaceove transformacije za diskretne sisteme.
To pomeni, da z uporabo Laplaceove transformacije (ali Z-transformacije, kot je potrebno) za funkcijo, ki opisuje želeni filter, zamenjavo enega v nastalega in transformacijo nazaj, dobimo impulzni odziv. Sliši se enostavno, vsak lahko poskusi. Ne bom tvegal, saj je, kot že omenjeno, Laplaceova transformacija huda stvar, sploh obratna. Pustimo to kot zadnjo možnost in poiščimo enostavnejše načine, da dobimo tisto, kar iščemo. Več jih je.
Najprej se lahko spomnimo še enega neverjetnega dejstva narave - amplitudno-frekvenčne in impulzne značilnosti so med seboj povezane z dobro in znano Fourierjevo transformacijo. To pomeni, da lahko narišemo poljuben frekvenčni odziv po svojem okusu, iz njega vzamemo inverzno Fourierjevo transformacijo (zvezno ali diskretno) in dobimo impulzni odziv sistema, ki jo izvaja. To je preprosto neverjetno!
To pa ne bo brez težav. Prvič, impulzni odziv, ki ga dobimo, bo najverjetneje neskončen (ne bom se spuščal v razlage, zakaj; tako deluje svet), zato se bomo morali prostovoljno odločiti, da ga na neki točki prekinemo (nastavitev za to točko je enako nič). A to se ne bo zgodilo kar tako - posledica tega bo, kot bi pričakovali, popačenje frekvenčnega odziva izračunanega filtra - postal bo valovit, frekvenčna meja pa zamegljena.
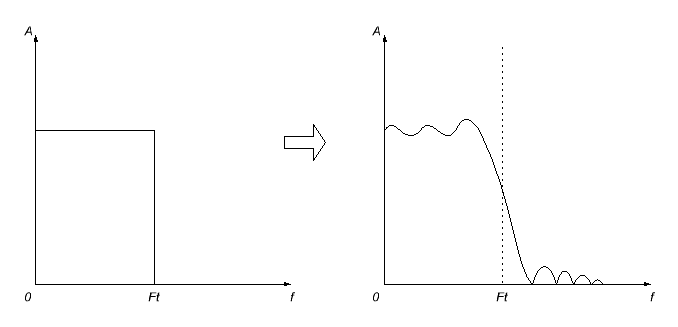
Za zmanjšanje teh učinkov se za skrajšan impulzni odziv uporabijo različne funkcije gladilnega okna. Zaradi tega je frekvenčni odziv navadno še bolj zamegljen, a neprijetna (predvsem v pasovnem pasu) nihanja izginejo. 
Pravzaprav po taki obdelavi dobimo delujoč impulzni odziv in lahko zgradimo digitalni filter.
Druga metoda izračuna je še preprostejša - impulzni odzivi najbolj priljubljenih filtrov so za nas že dolgo izraženi v analitični obliki. Vse, kar ostane, je, da nadomestite svoje vrednosti in uporabite funkcijo okna za rezultat po svojih željah. Tako vam sploh ni treba razmišljati o kakršnih koli preobrazbah.
In seveda, če je cilj posnemati vedenje določenega vezja, lahko dobite njegov impulzni odziv v simulatorju:
Tukaj sem uporabil impulz 100500 voltov (da, 100,5 kV) s trajanjem 1 μs na vhod vezja RC in dobil njegov impulzni odziv. Jasno je, da tega v resnici ni mogoče storiti, toda v simulatorju ta metoda, kot lahko vidite, deluje odlično.
5. Opombe.
Kar je bilo povedano zgoraj o skrajšanju impulznega odziva, je veljalo seveda za ti. filtri s končnim impulznim odzivom (FIR/FIR filtri). Imajo kup dragocenih lastnosti, vključno z linearno fazo (pod določenimi pogoji za konstrukcijo impulznega odziva), ki zagotavlja odsotnost popačenja signala med filtriranjem, pa tudi absolutno stabilnost. Obstajajo tudi filtri z neskončnim impulznim odzivom (IIR/IIR filtri). Z vidika izračunov so manj intenzivni, vendar nimajo več naštetih prednosti.
Upam, da bom v naslednjem članku pogledal preprost primer praktične izvedbe digitalnega filtra.
NOVOSIBIRSKA DRŽAVNA TEHNIČNA UNIVERZA
FAKULTETA ZA AVTOMATIKO IN RAČUNALNIŠTVO
Oddelek za sisteme zbiranja in obdelave podatkov
Disciplina "Teorija in obdelava signalov"
LABORATORIJSKO DELO ŠT.10
DIGITALNI FILTRI
S KARAKTERISTIKO KONČNEGA IMPULZA
Skupina: AT-33
možnost: 1 učiteljica:
Študent:Šadrina A.V. Izr. Ščetinin Ju.I.
Cilj dela: študij metod za analizo in sintezo filtrov s končnim impulznim odzivom z uporabo gladilnih okenskih funkcij.
Dokončanje dela:
1. Grafi impulznega odziva nizkopasovnega FIR filtra z mejno frekvenco pravokotnega okna za vrednosti dolžine filtra in .
Impulzni odziv idealnega diskretnega filtra FIR ima neskončno dolžino in je različen od nič za negativne vrednosti:
.
Da bi dobili fizično izvedljiv filter, bi morali omejiti impulzni odziv na končno število in nato za določeno količino premakniti okrnjeni odziv v desno.
Vrednost je dolžina (velikost) filtra, 
– vrstni red filtrov.
Skript Matlab (labrab101.m)
N = input("Vnesite dolžino filtra N = ");
h = sin(wc.*(n-(N-1)/2))./(pi.*(n-(N-1)/2));
xlabel("Referenčna številka, n")
>> podzaplet (2,1,1)
>> labrab101
Vnesite dolžino filtra N = 15
>> title("Impulzni odziv FIR filtra za N=15")
>> podzaplet (2,1,2)
>> labrab101
Vnesite dolžino filtra N = 50
>> title("Impulzni odziv FIR filtra za N=50")
Slika 1. Grafi impulznega odziva nizkopasovnega FIR filtra z mejno frekvenco pravokotnega okna za vrednosti dolžine filtra in
komentar:Če frekvenčni odziv digitalnega filtra obravnavamo kot Fourierjev niz: 
, potem bodo koeficienti te serije predstavljali vrednosti impulznega odziva filtra. V tem primeru je bila Fourierjeva serija v prvem primeru okrnjena na , v drugem pa na , nato pa so bile okrnjene karakteristike premaknjene vzdolž osi vzorca v desno, da bi dobili vzročni filter. Ko je širina glavnega režnja 2 in ko - 1, tj. Ko se dolžina filtra poveča, se glavni reženj impulznega odziva zoži. Če upoštevamo raven stranskih režnjev (z uporabo), se z naraščanjem povečuje v absolutni vrednosti od do . Tako lahko sklepamo, da je pri uporabi približka idealnega frekvenčnega odziva filtra s pravokotnim oknom nemogoče hkrati zožiti glavni reženj (in s tem zmanjšati prehodno območje) in zmanjšati nivoje stranskih reženj (zmanjšati valovanje v prepustnem in zaustavitvenem pasu filtra). Edini nadzirani parameter pravokotnega okna je njegova velikost, s katero lahko vplivamo na širino glavnega režnja, na stranska režnja pa nima velikega vpliva.
2. Izračun DVFT impulznih karakteristik iz koraka 1 z uporabo funkcije. Grafi njihovega frekvenčnega odziva na linearni skali in v decibelih za 512 frekvenčnih vzorcev. Prepustni pas, prehodni pas in zaporni pas filtra. Vpliv vrstnega reda filtra na širino prehodnega pasu in stopnjo valovanja frekvenčnega odziva v pasovih prehoda in zaustavitve.
Funkcija Matlab (DTFT.m)
funkcija = DTFT(x,M)
N = max(M, dolžina(x));
% Zmanjšanje FFT na velikost 2^m
N = 2^(ceil(log(N)/log(2)));
% Izračunaj ft
% Frekvenčni vektor
w = 2*pi*((0:(N-1))/N);
w = w - 2*pi*(w>=pi);
% Shift FFT za obseg od -pi do +pi
X = fftshift(X);
w = fftshift(w);
Skript Matlab (labrab102.m)
h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));
h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));
DTFT(h1,512);
DTFT(h2,512);
plot(w./(2*pi),abs(H1)./max(abs(H1)),,"r")
xlabel("f, Hz"), ylabel("|H1|/max(|H1|)"), mreža
plot(w./(2*pi),abs(H2)./max(abs(H2)),,"b")
xlabel("f, Hz"), ylabel("|H2|/max(|H2|)"), mreža
graf(w./(2*pi),20*log10(abs(H1)),,"r")
title("Frekvenčni odziv nizkopasovnega FIR filtra s pravokotnim oknom za N = 15")
xlabel("f, Hz"), ylabel("20lg(|H1|), dB"), mreža
graf(w./(2*pi),20*log10(abs(H2)),"b")
title("Frekvenčni odziv nizkopasovnega FIR filtra s pravokotnim oknom za N = 50")
xlabel("f, Hz"), ylabel("20lg(|H2|), dB"), mreža
Slika 2. Grafi frekvenčnega odziva nizkopasovnega FIR filtra z mejno frekvenco pravokotnega okna za vrednosti dolžine filtra in na linearni lestvici
Slika 3. Grafi frekvenčnega odziva nizkopasovnega FIR filtra z mejno frekvenco pravokotnega okna za vrednosti dolžine filtra in na logaritemskem merilu
komentar:
Tabela 1. Razpon prepustnega pasu, prehodnega območja in zaustavitvenega pasu za dolžino filtra in
|
Dolžina filtra |
Pasovna širina, Hz |
Območje prehoda, Hz |
Zaustavni pas, Hz |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Predavanje št. 10 "Digitalni filtri s končnim impulznim odzivom" Prenosno funkcijo fizično uresničljivega digitalnega filtra s končnim impulznim odzivom (FIR filter) lahko predstavimo kot (10.1). Pri zamenjavi v izrazu (10.1) dobimo frekvenčni odziv FIR filtra v obliki Kje Fazni zamik filter je opredeljen kot Skupinska zamuda filter je opredeljen kot Posebna značilnost filtrov FIR je zmožnost izvajanja konstantnih faznih in skupinskih zakasnitev, tj. linearni fazni odziv (10.5), kje - konstantno. Če je ta pogoj izpolnjen, signal, ki gre skozi filter, ne popači njegove oblike. Za izpeljavo pogojev, ki zagotavljajo linearni fazni odziv, zapišemo frekvenčni odziv FIR filtra ob upoštevanju (10.5) Z enačenjem realnega in namišljenega dela te enakosti dobimo Če drugo enačbo delimo s prvo, dobimo Končno lahko pišemo Ta enačba ima dve rešitvi. Prvič, ko a =0 ustreza enačbi Ta enačba ima edinstveno rešitev, ki ustreza poljubnemu h (0) (sin (0)=0) in h (n)=0 za n >0. Ta rešitev ustreza filtru, katerega impulzni odziv ima v začetnem času en sam vzorec, ki ni nič. Tak filter ni praktičnega pomena. Za to bomo našli drugo rešitev. V tem primeru z navzkrižnim množenjem števcev in imenovalcev v (10.8) dobimo (10.11). Od tu imamo Ker ima ta enačba obliko Fourierove vrste, je njena rešitev, če obstaja, edinstvena. Zlahka je videti, da mora rešitev te enačbe izpolnjevati pogoje (10.13), (10.14). Iz pogoja (10.13) sledi, da je za vsak red filtrov n obstaja samo ena fazna zamuda a , pri kateri je mogoče doseči strogo linearnost faznega odziva. Iz pogoja (10.14) sledi, da mora biti impulzni odziv filtra simetričen glede na točko za liho n , in glede na sredino intervala (slika 10.1).
Frekvenčni odziv takega filtra (za liho n ) lahko zapišemo v obliki (10.15). Izvedba zamenjave v drugem znesku m = N -1- n, dobimo (10.16). Ker je h (n) = h (N -1- n ), potem lahko obe vsoti združimo Zamenjamo, dobimo (10.18). Če določimo potem lahko končno pišemo Tako imamo za filter z linearnim faznim odzivom Za primer celo n podobno bomo imeli Če zamenjamo drugo vsoto, dobimo Izdelava zamenjave, dobimo (10.24). Po določitvi bomo končno imeli Tako za filter FIR z linearnim faznim odzivom in enakomernim vrstnim redom N lahko zapišemo V nadaljevanju bomo zaradi enostavnosti upoštevali samo filtre z lihim vrstnim redom. Pri sintezi prenosne funkcije filtra so začetni parametri praviloma zahteve za frekvenčni odziv. Obstaja veliko tehnik za sintezo FIR filtrov. Poglejmo jih nekaj. Ker je frekvenčni odziv katerega koli digitalnega filtra periodična funkcija frekvence, ga lahko predstavimo kot Fourierjev niz kjer sta koeficienta Fourierove vrste enaka Vidimo lahko, da so koeficienti Fourierove vrste h(n ) sovpadajo s koeficienti impulznega odziva filtra. Če je torej znan analitični opis zahtevanega frekvenčnega odziva filtra, potem je mogoče enostavno določiti koeficiente impulznega odziva in iz njih prenosno funkcijo filtra. Vendar v praksi to ni izvedljivo, saj je impulzni odziv takega filtra neskončno dolg. Poleg tega tak filter ni fizično izvedljiv, saj se impulzni odziv začne pri -¥ in nobena končna zamuda ne bo naredila tega filtra fizično izvedljivega. Ena od možnih metod za pridobitev filtra FIR, ki se približa danemu frekvenčnemu odzivu, je skrajšanje neskončnega Fourierovega niza in impulznega odziva filtra ob predpostavki, da h (n)=0 pri . Potem Fizična izvedljivost prenosne funkcije H(z ) lahko dosežete z množenjem H(z) na . Kje (10.32). S takšno spremembo prenosne funkcije se amplitudna karakteristika filtra ne spremeni, skupinska zakasnitev pa se poveča za konstantno količino. Kot primer izračunajmo nizkopasovni FIR filter s frekvenčnim odzivom oblike V skladu z (10.29) so koeficienti impulznega odziva filtra opisani z izrazom Zdaj lahko iz (10.31) dobimo izraz za prenosno funkcijo Kje (10.36). Amplitudne karakteristike izračunanega filtra za različne n so prikazani na sliki 10.2.
Slika 10.2 Valovanje v prepustnem in zaustavitvenem pasu se pojavi zaradi počasne konvergence Fourierjevega niza, ki je posledično posledica prisotnosti diskontinuitete v funkciji na mejni frekvenci prepustnega pasu. Te pulzacije so znane kot Gibbsovo valovanje. Iz slike 10.2 je jasno, da z naraščanjem n frekvenca pulziranja se poveča, amplituda pa zmanjša tako pri nižjih kot višjih frekvencah. Vendar amplituda zadnjega valovanja v prepustnem pasu in prvega valovanja v zavornem pasu ostane praktično nespremenjena. V praksi so takšni učinki pogosto nezaželeni, kar zahteva iskanje načinov za zmanjšanje Gibbsovih pulzacij. Okrajšan impulzni odziv h(n ) lahko predstavimo kot produkt zahtevanega neskončnega impulznega odziva in nekaj okenske funkcije w (n) dolžine n (slika 10.3).
V obravnavanem primeru enostavnega skrajšanja Fourierovega niza uporabimo pravokotno okno V tem primeru lahko frekvenčni odziv filtra predstavimo kot kompleksno konvolucijo To pomeni, da bo šlo za "zamegljeno" različico zahtevane lastnosti. Težava se zmanjša na iskanje okenskih funkcij, ki omogočajo zmanjšanje Gibbsovega valovanja z enako selektivnostjo filtra. Če želite to narediti, morate najprej preučiti lastnosti okenske funkcije na primeru pravokotnega okna. Spekter pravokotne okenske funkcije lahko zapišemo kot Spekter pravokotne okenske funkcije je prikazan na sliki 10.4.
Slika 10.4 Ker je pri , se izkaže, da je širina glavnega režnja spektra enaka . Prisotnost stranskih režnjev v spektru okenske funkcije povzroči povečanje Gibbsovega valovanja v frekvenčnem odzivu filtra. Da bi dosegli nizko valovanje v prepustnem pasu in veliko dušenje v zavornem pasu, je potrebno, da je območje, omejeno s stranskimi režnji, le majhen delež območja, omejenega z glavnim režnjem. Po drugi strani pa širina glavnega režnja določa širino prehodnega območja nastalega filtra. Za visoko selektivnost filtra mora biti širina glavnega režnja čim manjša. Kot je razvidno iz zgornjega, se širina glavnega režnja zmanjšuje z naraščajočim vrstnim redom filtra. Tako lahko lastnosti ustreznih okenskih funkcij formuliramo na naslednji način: - funkcija okna mora biti časovno omejena; - spekter okenske funkcije bi se moral najbolje približati frekvenčno omejeni funkciji, tj. imajo minimalno energijo zunaj glavnega režnja; - Širina glavnega režnja spektra okenskih funkcij mora biti čim manjša. Najpogosteje uporabljene okenske funkcije so: 1. Pravokotno okno. Omenjeno zgoraj. 2. Hammingovo okno. Kje . To okno se imenuje Hannovo okno ( hanning). 3. Blackmanovo okno. 4. Bartlettovo okno. Indikatorji filtrov, zgrajenih z uporabo določenih okenskih funkcij, so povzeti v tabeli 10.1.
Faktor valovanja je definiran kot razmerje med največjo amplitudo stranskega režnja in amplitudo glavnega režnja v spektru okenske funkcije. Za izbiro zahtevanega vrstnega reda filtrov in najprimernejše okenske funkcije pri izračunu realnih filtrov lahko uporabite podatke v tabeli 10.2.
Kot je razvidno iz tabele 10.1, obstaja določeno razmerje med koeficientom valovanja in širino glavnega režnja v spektru okenske funkcije. Manjši kot je pulzacijski koeficient, večja je širina glavnega režnja in s tem prehodno območje v frekvenčnem odzivu filtra. Za zagotovitev nizke valovitosti v prepustnem pasu je treba izbrati okno z ustreznim koeficientom valovanja in zagotoviti zahtevano širino prehodnega območja s povečanim filtrskim redom N. To težavo je mogoče rešiti z oknom, ki ga predlaga Kaiser. Funkcija Kaiserjevega okna ima obliko
kjer je a neodvisen parameter,
Privlačna lastnost Kaiserjevega okna je zmožnost gladkega spreminjanja koeficienta pulziranja od majhnih do velikih vrednosti, pri čemer se spremeni samo en parameter a. V tem primeru, tako kot pri drugih okenskih funkcijah, lahko širino glavnega režnja prilagodite z vrstnim redom filtrov N. Glavni parametri, nastavljeni pri razvoju pravega filtra, so: Pasovna širina - w p ; Trak z ovirami - w a ; Največja dopustna valovitost v prepustnem pasu je A p ; Najmanjše dušenje zavornega pasu – A a ; -frekvenca vzorčenja - ws. Ti parametri so prikazani na sliki 10.5. V tem primeru je največje valovanje v prepustnem pasu določeno kot
in minimalno slabljenje v zavornem pasu je kot Relativno preprost postopek za izračun filtra s Kaiserjevim oknom vključuje naslednje korake: 1. Določi se impulzni odziv filtra h (n), če je frekvenčni odziv idealen
kjer je (10.49). 2. Parameter d je izbran kot
Kje 3. Pravo vrednost A a in A p izračunamo z uporabo formul (10.46), (10.47). 4. Parameter a je izbran kot
5. Parameter D je izbran kot
6. Iz pogoja izberite najmanjšo liho vrednost vrstnega reda filtrov
temu sledi Ker so vzorci impulznega odziva filtra koeficienti njegove prenosne funkcije, pogoj (10.59) pomeni, da kode vseh koeficientov filtra vsebujejo le delni del in predznačni bit in ne vsebujejo celega dela. Število števk delnega dela koeficientov filtra se določi iz pogoja izpolnjevanja prenosne funkcije filtra s kvantiziranimi koeficienti, določenih zahtev za približevanje referenčni prenosni funkciji z natančnimi vrednostmi koeficientov. Absolutne vrednosti vzorcev vhodnega signala filtra so običajno normalizirane tako, da Če se analiza izvede za filter FIR z linearnim faznim odzivom, je lahko algoritem za izračun njegovega izhodnega signala naslednji kjer so koeficienti filtra zaokroženi na s k. Ta algoritem ustreza blokovnemu diagramu filtra, prikazanemu na sliki 10.5.
Obstajata dva načina za implementacijo tega algoritma. V prvem primeru so vse operacije množenja izvedene natančno in ni zaokroževanja produktov. V tem primeru je bitna globina produktov enaka s in + s k, kjer je s in bitna globina vhodnega signala, s k pa bitna globina koeficientov filtra. V tem primeru blokovni diagram filtra, prikazan na sliki 10.5, natančno ustreza dejanskemu filtru. Pri drugem načinu izvedbe algoritma (10.61) je vsak rezultat operacije množenja zaokrožen, tj. izdelki so izračunani z nekaj napake. V tem primeru je treba algoritem (10.61) spremeniti tako, da bo upošteval napako, ki nastane zaradi zaokroževanja produktov. Če se vzorčne vrednosti izhodnega signala filtra izračunajo s prvo metodo (z natančnimi vrednostmi produktov), se disperzija izhodnega hrupa določi kot
tiste. odvisno od variance hrupa zaokroževanja vhodnega signala in vrednosti koeficientov filtra. Tukaj lahko najdete zahtevano število bitov vhodnega signala kot
Z uporabo znanih vrednosti s in in s k lahko določimo število bitov, potrebnih za delni del kode izhodnega signala kot Če so vrednosti vzorcev izhodnega signala izračunane z uporabo druge metode, ko je vsak produkt zaokrožen na s d števk, potem lahko razpršitev hrupa zaokroževanja, ki ga ustvari vsak od množiteljev, izrazimo z zmogljivostjo števk izdelek kot DR in razmerje med signalom in šumom na izhodu filtra SNR out. Dinamični razpon vhodnega signala v decibelih je definiran kot
kjer sta A max in A min največji in najmanjši amplitudi vhodnega signala filtra. Razmerje med signalom in šumom na izhodu filtra, izraženo v decibelih, je definirano kot
določi povprečno kvadratno vrednost moči izhodnega sinusnega signala filtra z amplitudo A min in (10.77) določa moč šuma na izhodu filtra. Iz (10.75) in (10.76) z A max =1 dobimo izraz za disperzijo izhodnega šuma filtra To vrednost disperzije hrupa izhodnega filtra je mogoče uporabiti za izračun bitne globine vhodnih in izhodnih signalov filtra.  Svet brezplačnih programov in koristnih nasvetov 2024 whatsappss.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(10.2),
- amplitudno-frekvenčni odziv (AFC) filter,
- fazno-frekvenčni odziv (PFC) filter.
(10.3).
(10.4).
(10.6).
(10.7).
(10.8).
(10.9).
(10.10).
(10.12).
(10.17).
(10.19),
(10.20).
(10.21).
(10.22).
(10.23).
(10.25),
(10.26).
(10.27).
(10.28),
(10.29).
(10.30).
(10.31),
(10.33).
(10.34).
(10.35),
(10.37).
(10.38).
(10.39).
(10.40).
(10.41),
(10.42).
(10.43).
(10.44),
, I 0 – Besselova funkcija prve vrste ničelnega reda, definirana z izrazom
(10.45).
(10.46),
(10.50),
(10.51).
(10.52).
(10.53).
(10.54),
(10.57)
(10.66),
(10.67).
(10.74),
(10.75),
(10.78).