Filtra impulsa reakcija. Digitālie filtri ar ierobežotu impulsu reakciju. Datu izlīdzināšana. Vidējā filtrēšana
48 Digitālie filtri ar ierobežotu impulsu reakciju. Kih filtru aprēķins.
Ierobežotu impulsu atbildes filtrs (Nerekursīvs filtrs, FIR filtrs) vai FIR filtrs (FIR ir saīsināts no ierobežota impulsa reakcija - ierobežota impulsa reakcija) - viens no lineāro digitālo filtru veidiem, kura raksturīga iezīme ir laika ierobežojums impulsa reakcija(no kāda laika tas kļūst tieši vienāds ar nulli). Šādu filtru sauc arī par nerekursīvu atgriezeniskās saites trūkuma dēļ. Šāda filtra pārneses funkcijas saucējs ir noteikta konstante.
Atšķirības vienādojums, kas apraksta attiecības starp filtra ieejas un izejas signāliem: kur P- filtru secība, x(n) - ievades signāls, y(n) ir izejas signāls un b i- filtra koeficienti. Citiem vārdiem sakot, jebkura izejas signāla parauga vērtību nosaka mērogoto vērtību summa P iepriekšējie lasījumi. Jūs varat teikt savādāk: filtra izejas vērtība jebkurā brīdī ir reakcijas vērtība uz ieejas momentāno vērtību un visu pakāpeniski dilstošo reakciju summa. P iepriekšējie signāla paraugi, kas joprojām ietekmē izvadi (pēc P-skaita, impulsa pārejas funkcija kļūst vienāda ar nulli, kā jau minēts, tāpēc visi termini pēc P-th arī kļūs vienāds ar nulli). Uzrakstīsim iepriekšējo vienādojumu ietilpīgākā formā:
Lai atrastu filtra kodolu, ko mēs ievietojām
x(n) = δ( n)
kur δ( n) - delta funkcija. Tad FIR filtra impulsa reakciju var uzrakstīt šādi:
Impulsa reakcijas Z-transformācija dod mums FIR filtra pārsūtīšanas funkciju:
]Īpašības
FIR filtram ir vairākas noderīgas īpašības, kuru dēļ dažreiz ir vēlams to izmantot nekā IIR filtru. Šeit ir daži no tiem:
FIR filtri ir izturīgi.
FIR filtriem nav nepieciešama atgriezeniskā saite, kad tie tiek ieviesti.
FIR filtru fāzi var padarīt lineāru
Tiešā FIR filtra forma
FIR filtrus var ieviest, izmantojot trīs elementus: reizinātāju, summatoru un aizkaves bloku. Attēlā redzamā opcija ir tieša 1. tipa FIR filtru ieviešana.
FIR filtra tiešās formas ieviešana
Programmas piemērs
Tālāk ir parādīts C valodā rakstīts FIR filtra programmas piemērs:
/* FIR filtrs 128 krāniem */
float fir_filter(peldošā ievade)
statiskais pludiņa paraugs;
acc = 0,0f; /* Akumulators */
/* Reizināt un uzkrāt */
par (i = 0; i< 128; i++) {
acc += (h[i] * paraugs[i]);
/* Izeja */
/* Pārslēdziet aizkavēto signālu */
par (i = 127; i > 0; i--)
paraugs[i] = paraugs;
49 Datu izlīdzināšana. Kustīgais vidējais rādītājs.
50 Datu izlīdzināšana. Paraboliska izlīdzināšana.
51 Datu izlīdzināšana. Spensera izlīdzināšana.
52 Datu izlīdzināšana. Vidējā filtrēšana.
Kustīgā vidējā noteikšana, paraboliskā izlīdzināšana, Spencera izlīdzināšana, vidējā filtrēšana
Izstrādājot metodes fizikālo procesu, kas laika gaitā lēnām mainās, parametru noteikšanai, svarīgs uzdevums ir novērst trokšņu efektu vai nejaušu traucējumu ietekmi, kas tiek uzklāta uz apstrādāto signālu, kas saņemts primārā pārveidotāja izejā.
Lai novērstu šo efektu, varat izmantot datu izlīdzināšanu. Viena no vienkāršākajām šādas izlīdzināšanas metodēm ir aritmētiskā vidējā aprēķināšana. Izmantojot to, katra diskrētās funkcijas (apstrādāto datu masīva) vērtība tiek aprēķināta saskaņā ar izteiksmi:
kur ir punktu skaits aritmētiskajai vidējai aprēķināšanai (nepāra vesels skaitlis);
Funkcijas vērtība pirms apstrādes;
Ir arī citas diezgan efektīvas izlīdzināšanas metodes, piemēram, ar otrās pakāpes parabolām piecos, septiņos, deviņos un vienpadsmit punktos saskaņā ar izteicieniem:
vai ceturtās pakāpes parabolas septiņos, deviņos, vienpadsmit un trīspadsmit punktos:
Praktiskā pielietojumā labus rezultātus dod citas efektīvas metodes, piemēram, 15 punktu Spencer izlīdzināšana:
Aizvietojot komplekso eksponenciālo , kur šajās izteiksmēs, mēs varam noteikt atbilstošās transformācijas pārneses funkciju.
Vidējai aritmētiskai
Izteiksme iekavās attēlo ģeometrisku progresiju ar saucēju, tāpēc šo izteiksmi var attēlot šādi:
.
Šī formula atspoguļo zemas caurlaidības filtra pārvades raksturlielumu, un tā parāda, ka jo vairāk terminu ir iesaistīti vidējā aprēķināšanā, jo lielāka signāla augstfrekvences trokšņu komponentu slāpēšana (sk. 6.1. attēlu).
Tomēr frekvences semantiskais jēdziens, apstrādājot laika tendences, atšķiras no līdzīgas koncepcijas, apstrādājot signālus. Tas izskaidrojams ar to, ka, pētot laika tendences, interesē nevis to biežuma sastāvs, bet gan izmaiņu veids (pieaugums, samazinājums, nemainīgums, cikliskums utt.).
Arī tā saukto heiristisko algoritmu izmantošana ir diezgan efektīva datu izlīdzināšanai.
Viens no tiem ir vidējā filtrēšana. Tās realizācijas laikā dimensijas slīdošā laika logā, kur vesels skaitlis ir nepāra skaitlis, centrālais elements tiek aizstāts ar secības vidējo elementu, kas vērtību augošā secībā ir sakārtoti izlīdzinātās datu masīva elementi. signāls, kas iekrīt laika logā. Vidējās filtrēšanas priekšrocība ir spēja noņemt impulsu troksni, kura ilgums nepārsniedz, praktiski neizkropļojot vienmērīgi mainīgus signālus. Šai trokšņu slāpēšanas metodei nav stingra matemātiska pamatojuma, taču aprēķinu vienkāršība un iegūto rezultātu efektivitāte ir novedusi pie tās plašas izmantošanas.
Attēls 6.1. Pārsūtīšanas raksturlielumu diagrammas
aritmētiskās vidējās darbības, ja m=5, 7, 9, 11
Vēl viens interesants izlīdzināšanas algoritms ir vidējā vidējā aprēķināšana. Tās būtība ir šāda. Bīdāmā laika logā ar lielumu (-nepāra vesels skaitlis) datu masīva elementi tiek sakārtoti augošā secībā, un pēc tam pirmais un pēdējais elementi tiek noņemti no sakārtotās secības (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
Šī metode ļauj nomākt impulsu un radiofrekvenču traucējumus, kā arī panākt labu signāla izlīdzināšanu.
| " |
Apskatīsim vienkāršākos digitālos filtrus - filtrus ar nemainīgiem parametriem.
Digitālā filtra ieejas signāls tiek piegādāts skaitlisko vērtību secības veidā, kas seko intervāliem (4.1. att., a). Saņemot katru nākamo signāla vērtību ciparu filtrā, tiek aprēķināta nākamā izejas signāla vērtība.Aprēķinu algoritmi var būt ļoti dažādi; aprēķina procesā papildus ieejas signāla pēdējai vērtībai var izmantot
iepriekšējās ieejas un izejas signālu vērtības: digitālā filtra izejas signāls ir arī skaitlisko vērtību secība, kas seko intervālam . Šis intervāls ir vienāds visai digitālā signāla apstrādes ierīcei.
Rīsi. 4.1. Signāls pie digitālā filtra ieejas un izejas
Tāpēc, ja vienkāršāko signālu viena impulsa veidā pieliekat digitālā filtra ieejai (4.2. att., a)
tad izejā mēs saņemam signālu diskrētas skaitlisko vērtību secības formā, kas seko intervāliem
Pēc analoģijas ar parastajām analogajām shēmām šo atbildes signālu sauksim par filtra impulsa reakciju (4.2. att., b). Atšķirībā no analogās ķēdes impulsa reakcijas, funkcija ir bezizmēra.
Rīsi. 4.2. Vienības impulss un digitālā filtra impulsa reakcija
Pielietosim patvaļīgu diskrētu signālu filtra ieejai (att. 4.1, a), kas ir diskrētu vērtību kopa
Pirmā elementa darbības rezultātā filtra izejā tiek veidota secība, kas reizināta ar; darbības laikā secība tiek reizināta ar un nobīdīta pa labi ar summu utt. Rezultātā izvade iegūs secība kur
Tādējādi izejas signāls tiek definēts kā ieejas signāla un impulsa reakcijas diskrēta konvolūcija. Šajā ziņā digitālie filtri ir līdzīgi parastajām shēmām, kur izejas signāls ir vienāds ar ieejas signāla un impulsa reakcijas konvolūciju.
Formula (4.1) ir ciparu filtrēšanas algoritms. Ja filtra impulsa reakciju apraksta secība ar ierobežotu skaitu terminu, tad filtru var realizēt shēmas veidā, kas parādīts attēlā. 4.3. Šeit burts norāda signāla aizkaves elementus uz laiku (vienā šūnā); -elementi, kas reizina signālu ar atbilstošo koeficientu.
Attēlā parādītā diagramma. 4.3 nav digitālā filtra elektriskā ķēde; Šī diagramma ir digitālā filtrēšanas algoritma grafisks attēlojums un parāda signālu apstrādes laikā veikto aritmētisko darbību secību.
Rīsi. 4.3. Nerekursīva digitālā filtra shēma
Digitālajiem filtriem, kas apstrādā signālus abstraktu ciparu secību veidā, jēdziens “laika aizkave” nav pilnīgi pareizs. Tāpēc elementi, kas aizkavē signālu par vienu šūnu, parasti tiek atzīmēti uz digitālo filtru shēmām ar simbolu, kas norāda signāla aizkavi -transformāciju valodā. Turpmāk mēs pieturēsimies pie šī apzīmējuma.
Atgriezīsimies pie digitālā filtra shēmas, kas parādīta attēlā. 4.3. Tādus filtrus, kuros aprēķiniem izmanto tikai ieejas signāla vērtības, sauc par vienkāršiem vai nerekursīviem.
Nerekursīvo filtru algoritmu ir viegli uzrakstīt, ja ir zināma filtra impulsa reakcija. Algoritma praktiskai īstenošanai nepieciešams, lai impulsa atbilde satur noteiktu skaitu terminu. Ja impulsa atbilde satur bezgalīgu skaitu terminu, bet to vērtība ātri samazinās, varat aprobežoties ar ierobežotu terminu skaitu, atmetot tos, kuru vērtības ir mazas. Ja impulsa reakcijas elementu vērtība nesamazinās, nerekursīvais filtra algoritms izrādās nerealizējams.
Rīsi. 4.4. - ķēde
Kā piemēru apsveriet vienkāršāko digitālo filtru, kas ir līdzīgs -ķēdei (4.4. att.). Ķēdes impulsa reakcijai ir forma
Lai uzrakstītu atbilstošā digitālā filtra impulsa reakciju, izteiksme jāaizstāj ar. Tomēr ķēdes impulsa reakcijai ir dimensija, un digitālā filtra impulsa reakcijai jābūt bezizmēra. Tāpēc izteiksmē (4.2) izlaižam reizinātāju un formā ierakstām digitālā filtra impulsa reakciju
Šāda impulsa reakcija satur bezgalīgi daudz terminu, bet to lielums samazinās saskaņā ar eksponenciālu likumu, un mēs varam aprobežoties ar terminiem, izvēloties tādus,
Tagad mēs varam ierakstīt signāla izteiksmi filtra izejā
Šī izteiksme ir arī digitālā filtra algoritms. Šī filtra diagramma ir parādīta attēlā. 4.5.
Otrā pieeja procesu analīzei digitālajos filtros ir līdzīga operatora metodei parasto analogo ķēžu analīzei, tikai Laplasa transformācijas vietā tiek izmantota -transformācija.
Rīsi. 4.5. Nerekursīva digitālā filtra shēma, kas līdzīga -ķēdei
Definēsim digitālā filtra parametru, kas ir līdzīgs elektriskās ķēdes pārsūtīšanas funkcijai. Lai to izdarītu, veiciet transformāciju digitālā filtra impulsa reakcijai:
Funkciju sauc par sistēmas filtra funkciju.
Saskaņā ar izteiksmi (4.1.) signāls digitālā filtra izejā ir vienāds ar ieejas signāla diskrēto konvolūciju un filtra impulsa reakciju. Piemērojot šai izteiksmei konvolūcijas teorēmu, iegūstam, ka izejas signāla transformācija ir vienāda ar ieejas signāla transformāciju, kas reizināta ar sistēmas filtra funkciju:
Tādējādi sistēmas funkcija spēlē digitālā filtra pārsūtīšanas funkciju.
Piemēram, atradīsim pirmās kārtas digitālā filtra sistēmas funkciju, kas ir līdzīga -ķēdei:
Trešā metode, kā analizēt signālu pāreju caur digitālajiem filtriem, ir līdzīga klasiskajai diferenciālvienādojumu metodei. Apskatīsim šo metodi, kā piemēru izmantojot pasūtījumu ķēdes.
Vienkāršākā 1. kārtas analogā shēma ir -ķēde (skat. 4.4. att.), caur kuru signālu pāreju raksturo diferenciālvienādojums.
Diskrētajai shēmai diferenciālvienādojuma (4.8) vietā jāraksta atšķirības vienādojums, kur ieejas un izejas signāli ir norādīti diskrētiem laika momentiem, bet atvasinājuma vietā - blakus signālu vērtību starpība. parādās. Diskrētai pirmās kārtas ķēdei atšķirības vienādojumu var uzrakstīt diezgan vispārīgā formā
Piemērosim transformāciju vienādojumam
kur atrodam sistēmas filtra funkciju
Formula (4.10) ir diezgan vispārīga pirmās kārtas digitālā filtra sistēmas funkcijas izteiksme. Kad tas sakrīt ar iepriekš iegūto izteiksmi (4.7) ciparu filtra sistēmas funkcijai, kas ekvivalenta -ķēdei.
Atradīsim sistēmas funkcijai atbilstošu digitālās filtrēšanas algoritmu (4.10). Lai to izdarītu, mēs atrisinām vienādojumu (4.9).
Šī algoritma ekvivalenta diagramma ir parādīta attēlā. 4.6. Salīdzinot ar nerekursīvo filtru (sk. 4.5. att.), šeit ir pievienota sava veida “atgriezeniskās saites ķēde”, kas nozīmē, ka izejas signāla vērtības tiek izmantotas turpmākajos
Rīsi. 4.6. Rekursīva digitālā filtra shēma, kas līdzīga -ķēdei
aprēķinus. Šāda veida filtrus sauc par rekursīviem.
Algoritms (4.11) atbilst filtram, kas ir pilnībā līdzvērtīgs iepriekš aplūkotajam nerekursīvajam filtram. Bet, lai noteiktu vienu izejas signāla vērtību, izmantojot nerekursīvo filtru algoritmu (4.4), ir jāveic darbības, un, izmantojot rekursīvā filtra algoritmu (4.11), ir nepieciešamas tikai divas darbības. Šī ir galvenā rekursīvo filtru priekšrocība. Turklāt rekursīvie filtri nodrošina signālu apstrādi ar lielāku precizitāti, jo tie ļauj pareizāk īstenot impulsa reakciju, neizmetot tās “aste”. Rekursīvie filtri ļauj ieviest algoritmus, kurus vispār nevar realizēt, izmantojot nerekursīvos filtrus. Piemēram, ar filtru, kas darbojas saskaņā ar shēmu attēlā. 4.6, būtībā ir ideāls akumulators-integrators un tam ir formas impulsa reakcija. Filtru ar šādu raksturlielumu nevar realizēt, izmantojot nerekursīvu shēmu.
Aplūkotie piemēri parāda, ka nav jēgas izmantot nerekursīvus algoritmus, lai izveidotu digitālos filtrus ar ilgu impulsa reakciju. Šādos gadījumos piemērotāk ir izmantot rekursīvos filtrus.
Nerekursīvo algoritmu pielietošanas joma ir digitālo filtru ieviešana ar impulsa reakciju, kas satur nelielu skaitu terminu. Piemērs ir vienkāršākais diferenciators, kura izejas signāls ir vienāds ar ieejas signāla pieaugumu:
Šāda digitālā filtra shēma ir parādīta attēlā. 4.7.
Rīsi. 4.7. Vienkāršākā digitālā diferenciatora shēma
Tagad apskatīsim vispārīgu digitālo filtru, ko apraksta vienādojums
Šo vienādojumu var uzskatīt gan par secības diferenciācijas vienādojumu, gan par digitālo filtrēšanas algoritmu, ja tas tiek pārrakstīts savādāk, proti,
Rīsi. 4.8. Rekursīva digitālā pasūtījuma filtra shēma
Algoritms (4.13) atbilst shēmai, kas parādīta attēlā. 4.8. Ļaujiet mums atrast šāda filtra sistēmas funkciju. Lai to izdarītu, piemērojiet transformāciju vienādojumam:
Izteiksme (4.14) ļauj izveidot savienojumu starp filtra ķēdes elementu svārstībām un sistēmas funkciju. Koeficienti sistēmas funkcijas skaitītājā nosaka koeficientu vērtības
(filtra nerekursīvajā daļā), un koeficienti saucējā nosaka filtra rekursīvo daļu.
Viss sākās, kad drauga drauga draugam bija nepieciešama palīdzība ar šiem pašiem filtriem. Caur Jedi ceļiem mani sasniedza baumas par to, es anulēju abonēšanu komentāros pie ziņas pie saites. Šķita, ka tas palīdzēja. Nu ceru.
Šis stāsts manī uzjundīja atmiņas par trešo vai kaut ko tamlīdzīgu kursu, kad es pats paņēmu DSP, un pamudināja uzrakstīt rakstu visiem tiem, kurus interesē digitālo filtru darbība, bet kurus, protams, baidās pāri. -top formulas un psihedēliskie zīmējumi iekšā (es jau nerunāju par mācību grāmatām).
Kopumā, pēc manas pieredzes, situāciju ar mācību grāmatām raksturo labi zināmā frāze, ka dažreiz mežu kokiem neredz. Un tā sakot, kad viņi uzreiz sāk biedēt ar Z-transformāciju un polinomu dalīšanas formulām, kas bieži vien ir garākas par diviem dēļiem, interese par tēmu ļoti ātri izžūst. Sāksim ar vienkāršu; par laimi, lai saprastu, kas notiek, nav nepieciešams aprakstīt garus sarežģītus izteicienus.
Tātad, pirmkārt, daži vienkārši pamatjēdzieni.
1. Impulsu reakcija.
Pieņemsim, ka mums ir kaste ar četrām tapām. Mums nav ne jausmas, kas atrodas iekšā, taču mēs noteikti zinām, ka divi kreisie termināļi ir ieeja, bet divi labie ir izeja. Mēģināsim uzlikt tam ļoti īsu impulsu ar ļoti lielu amplitūdu un redzēsim, kas notiek izejā. Nu, nav skaidrs, kas atrodas šajā kvadripolā, jo nav skaidrs, kā to aprakstīt, bet vismaz mēs kaut ko redzēsim.
Šeit jāsaka, ka īsu (vispārīgi runājot, bezgalīgi īsu) impulsu ar lielu (vispārīgi runājot, bezgalīgu) amplitūdu teorētiski sauc par delta funkciju. Starp citu, jocīgākais ir tas, ka šī sastāvdaļa ir bezgalīgs funkcija ir vienāda ar vienu. Tā ir normalizācija.
Tātad tas, ko mēs redzējām kvadripola tīkla izejā, pielietojot ieejai delta funkciju, tiek saukts impulsa reakcijašis četrstūris. Pagaidām gan nav skaidrs, kā tas mums palīdzēs, bet atcerēsimies iegūto rezultātu un pāriesim pie nākamās interesantās koncepcijas.
2. Konvolūcija.
Īsāk sakot, konvolūcija ir matemātiska darbība, kas ir saistīta ar funkciju produkta integrāciju:
Kā redzat, tas ir norādīts ar zvaigznīti. Varat arī redzēt, ka konvolūcijas laikā viena funkcija tiek uzņemta tās “uz priekšu” secībā, un mēs ejam cauri otrai “no aizmugures uz priekšu”. Protams, diskrētā gadījumā, kas cilvēcei ir vērtīgāks, konvolūcija, tāpat kā jebkurš integrālis, tiek summēts:
Šķiet, ka tā ir kaut kāda blāva matemātiskā abstrakcija. Tomēr patiesībā kūlis, iespējams, ir šīs pasaules maģiskākā parādība, kas apbrīnojamā ziņā ir otrajā vietā aiz cilvēka dzimšanas, ar vienīgo atšķirību, ka lielākā daļa cilvēku vismaz līdz gadu vecumam uzzina, no kurienes nāk bērni. astoņpadsmit, savukārt par to, kas ir konvolūcija un kāpēc tā ir noderīga un pārsteidzoša, lielai daļai Zemes iedzīvotāju visu mūžu nav ne mazākās nojausmas.
Tātad šīs operācijas spēks slēpjas faktā, ka, ja f ir jebkurš patvaļīgs ievades signāls un g ir četru portu tīkla impulsa reakcija, tad šo divu funkciju konvolūcijas rezultāts būs līdzīgs tam, ko mēs vēlētos iegūt, izlaižot signālu f caur šo četru portu tīklu.
Tas ir, impulsa reakcija ir pilnīgs visu četru portu tīkla īpašību kopums saistībā ar ieejas efektu, un ieejas signāla konvolūcija ar to ļauj atjaunot atbilstošo izejas signālu. Manuprāt, tas ir vienkārši pārsteidzoši!
3. Filtri.
Ar impulsa reakciju un konvolūciju var paveikt daudz interesantu lietu. Piemēram, ja signāls ir audio, varat organizēt reverbu, atbalsi, kori, flangeru un daudz ko citu; var atšķirt un integrēt... Kopumā var izveidot jebko. Mums šobrīd svarīgākais ir tas, ka, protams, filtrus var viegli iegūt arī izmantojot konvolūciju.
Pats digitālais filtrs ir ieejas signāla konvolūcija ar impulsa reakciju, kas atbilst vēlamajam filtram.
Bet, protams, impulsa reakcija kaut kā ir jāiegūst. Mēs, protams, jau iepriekš esam izdomājuši, kā to izmērīt, taču šādā uzdevumā no tā ir maz jēgas - ja mēs jau esam salikuši filtru, kāpēc vēl kaut ko mērīt, mēs to varam izmantot tādu, kāds ir. Un turklāt digitālo filtru vissvarīgākā vērtība ir tā, ka tiem var būt īpašības, kas patiesībā ir nesasniedzamas (vai ļoti grūti sasniedzamas) - piemēram, lineārā fāze. Tātad šeit vispār nav iespējams izmērīt, ir tikai jāskaita.
4. Impulsa reakcijas iegūšana.
Šajā brīdī lielākajā daļā publikāciju par šo tēmu autori sāk izgāzt lasītājam Z-transformāciju un polinomu frakciju kalnus, pilnībā mulsinot viņu. Es to nedarīšu, tikai īsi paskaidrošu, par ko tas viss ir un kāpēc praksē tas progresīvajai sabiedrībai nav īpaši nepieciešams.
Pieņemsim, ka esam izlēmuši, ko vēlamies no filtra, un izveidojuši vienādojumu, kas to apraksta. Tālāk, lai atrastu impulsa reakciju, atvasinātajā vienādojumā varat aizstāt delta funkciju un iegūt vajadzīgo. Vienīgā problēma ir, kā to izdarīt, jo delta funkcija ir laikā O th reģionu dod viltīga sistēma, un vispār ir visādas bezgalības. Tāpēc šajā posmā viss izrādās šausmīgi grūti.
Šeit gadās, ka viņi atceras, ka ir tāda lieta kā Laplasa transformācija. Pati par sevi tā nav ne mārciņa rozīņu. Vienīgais iemesls, kāpēc tas tiek pieļauts radiotehnikā, ir tieši tas, ka argumenta telpā, uz kuru šī transformācija ir pāreja, dažas lietas faktiski kļūst vienkāršākas. Jo īpaši tā pati delta funkcija, kas mums radīja tik daudz problēmu laika jomā, ir ļoti viegli izteikta - tur tā ir tikai viena!
Z-transformācija (pazīstama arī kā Laurent transformācija) ir Laplasa transformācijas versija diskrētām sistēmām.
Tas ir, piemērojot Laplasa transformāciju (vai Z-transformāciju, ja nepieciešams) funkcijai, kas apraksta vēlamo filtru, aizstājot vienu ar iegūto filtru un pārveidojot atpakaļ, mēs iegūstam impulsa reakciju. Tas izklausās vienkārši, ikviens var to izmēģināt. Es neriskēšu, jo, kā jau minēts, Laplasa transformācija ir skarba lieta, īpaši apgrieztā. Atstāsim to kā pēdējo līdzekli, un mēs meklēsim dažus vienkāršākus veidus, kā iegūt to, ko meklējam. Tādas ir vairākas.
Pirmkārt, mēs varam atgādināt vēl vienu pārsteidzošu dabas faktu - amplitūdas-frekvences un impulsa raksturlielumi ir saistīti viens ar otru ar labo un pazīstamo Furjē transformāciju. Tas nozīmē, ka mēs varam izdarīt jebkuru frekvences reakciju pēc savas gaumes, ņemt no tās apgriezto Furjē transformāciju (vai nu nepārtrauktu, vai diskrētu) un iegūt tās sistēmas impulsa reakciju, kas to īsteno. Tas ir vienkārši pārsteidzošs!
Tomēr tas neiztiks bez problēmām. Pirmkārt, impulsa reakcija, ko mēs saņemsim, visticamāk, būs bezgalīga (es neiedziļināšos paskaidrojumos, kāpēc; tā pasaule darbojas), tāpēc mums būs jāpieņem labprātīgs lēmums to pārtraukt kādā brīdī (iestatījums tas ir vienāds ar nulli aiz šī punkta). Bet tas nenotiks tāpat vien - tā sekas, kā varētu sagaidīt, būs aprēķinātā filtra frekvences reakcijas izkropļojumi - tas kļūs viļņains, un frekvences nogrieznis būs izplūdis.
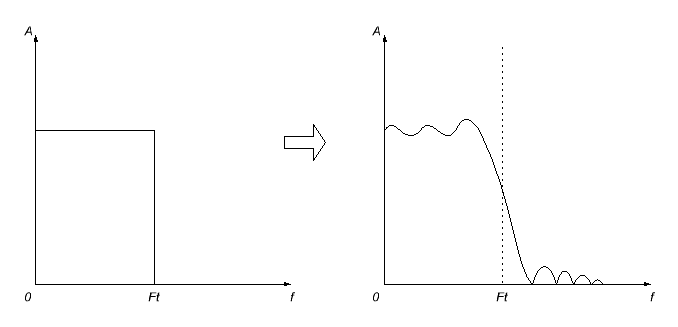
Lai samazinātu šos efektus, saīsinātajai impulsa reakcijai tiek piemērotas dažādas izlīdzināšanas loga funkcijas. Rezultātā frekvences reakcija parasti ir vēl vairāk izplūdusi, bet nepatīkamās (īpaši caurlaides joslā) svārstības pazūd. 
Faktiski pēc šādas apstrādes mēs iegūstam darba impulsa reakciju un varam izveidot digitālo filtru.
Otrā aprēķina metode ir vēl vienkāršāka - populārāko filtru impulsu reakcijas mums jau sen ir izteiktas analītiskā formā. Atliek tikai aizstāt savas vērtības un izmantot loga funkciju rezultātam pēc saviem ieskatiem. Tātad jums pat nav jāapsver nekādas pārvērtības.
Un, protams, ja mērķis ir atdarināt noteiktas ķēdes uzvedību, simulatorā varat iegūt tās impulsa reakciju:
Šeit es ievadīju 100500 voltu impulsu (jā, 100,5 kV) ar ilgumu 1 μs RC ķēdes ieejai un ieguvu tā impulsa reakciju. Ir skaidrs, ka patiesībā to nevar izdarīt, taču simulatorā šī metode, kā redzat, darbojas lieliski.
5. Piezīmes.
Iepriekš teiktais par impulsa reakcijas saīsināšanu attiecās, protams, uz t.s. ierobežotas impulsa atbildes filtri (FIR/FIR filtri). Viņiem ir virkne vērtīgu īpašību, tostarp lineārā fāze (noteiktos impulsa reakcijas konstruēšanas apstākļos), kas nodrošina signāla kropļojumu neesamību filtrēšanas laikā, kā arī absolūtu stabilitāti. Ir arī bezgalīgas impulsu atbildes filtri (IIR/IIR filtri). Tie ir mazāk resursietilpīgi aprēķinu ziņā, taču tiem vairs nav uzskaitīto priekšrocību.
Nākamajā rakstā ceru aplūkot vienkāršu digitālā filtra praktiskās ieviešanas piemēru.
NOVOSIBIRSKAS VALSTS TEHNISKĀ UNIVERSITĀTE
AUTOMATIZĀCIJAS UN DATORINženieru fakultāte
Datu vākšanas un apstrādes sistēmu katedra
Disciplīna "Teorija un signālu apstrāde"
LABORATORIJAS DARBS NR.10
DIGITĀLIE FILTRI
AR BEIGTA IMPULSU RAKSTUROJUMS
Grupa: AT-33
Iespēja: 1 Skolotājs:
Students:Šadrina A.V. Asoc. Shchetinin Yu.I.
Darba mērķis: galīgo impulsu atbildes filtru analīzes un sintēzes metožu izpēte, izmantojot izlīdzināšanas loga funkcijas.
Darba pabeigšana:
1. Zemas caurlaidības FIR filtra impulsa reakcijas diagrammas ar taisnstūra loga nogriešanas frekvenci filtra garuma vērtībām un .
Ideāla diskrēta FIR filtra impulsa reakcijai ir bezgalīgs garums un tā nav nulle negatīvām vērtībām:
.
Lai iegūtu fiziski īstenojamu filtru, impulsa reakcija jāierobežo līdz ierobežotam skaitlim un pēc tam saīsinātā atbilde jāpārvieto pa labi par summu.
Vērtība ir filtra garums (izmērs), 
- filtru secība.
Matlab skripts (labrab101.m)
N = ievade("Ievadiet filtra garumu N = ");
h = sin(wc.*(n-(N-1)/2))./(pi.*(n-(N-1)/2));
xlabel("Atsauces numurs, n")
>> apakšgabals(2,1,1)
>> labrab101
Ievadiet filtra garumu N = 15
>> title("FIR filtra impulsa reakcija N=15")
>> apakšgabals(2,1,2)
>> labrab101
Ievadiet filtra garumu N = 50
>> title("FIR filtra impulsa reakcija N=50")
1. att. Zemas caurlaidības FIR filtra impulsa reakcijas diagrammas ar taisnstūra loga nogriešanas frekvenci filtra garuma vērtībām un
Komentārs: Ja mēs uzskatām digitālā filtra frekvences reakciju kā Furjē sēriju: 
, tad šīs sērijas koeficienti atspoguļos filtra impulsa reakcijas vērtības. Šajā gadījumā Furjē sērija tika saīsināta pirmajā gadījumā līdz , bet otrajā - līdz , un pēc tam saīsinātie raksturlielumi tika nobīdīti pa parauga asi pa labi, lai iegūtu cēloņsakarības filtru. Kad galvenās daivas platums ir 2, un kad - 1, t.i. Palielinoties filtra garumam, impulsa reakcijas galvenā daiva sašaurinās. Ja ņemam vērā sānu daivu līmeni (izmantojot ), tad, palielinoties, tas absolūtajā vērtībā palielinās no līdz . Tādējādi mēs varam secināt, ka, izmantojot filtra ar taisnstūra logu ideālās frekvences reakcijas tuvinājumu, nav iespējams vienlaikus sašaurināt galveno daivu (un tādējādi samazināt pārejas reģionu) un samazināt sānu daivu līmeni (samazināt viļņošanās filtra caurlaides joslā un apturēšanas joslā). Vienīgais regulējamais taisnstūra loga parametrs ir tā izmērs, ar kuru var ietekmēt galvenās daivas platumu, taču tas īpaši neietekmē sānu daivas.
2. Impulsu raksturlielumu DVFT aprēķins no 1. soļa, izmantojot funkciju. To frekvences reakcijas grafiki lineārā mērogā un decibelos par 512 frekvences paraugi. Filtra caurlaides josla, pārejas josla un apturēšanas josla. Filtru secības ietekme uz pārejas joslas platumu un frekvences reakcijas pulsācijas līmeni caurlaides un apturēšanas joslās.
Matlab funkcija (DTFT.m)
funkcija = DTFT(x,M)
N = max(M, garums(x));
% FFT samazināšana līdz 2^m izmēram
N = 2^(griesti(log(N)/log(2)));
% Aprēķināt fft
% Frekvences vektors
w = 2*pi*((0:(N-1))/N);
w = w - 2*pi*(w>=pi);
% Shift FFT diapazonā no -pi līdz +pi
X = fftshift(X);
w = fftshift(w);
Matlab skripts (labrab102.m)
h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));
h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));
DTFT(h1,512);
DTFT(h2,512);
diagramma(w./(2*pi),abs(H1)./maks.(abs(H1)),"r")
xlabel("f, Hz"), ylabel("|H1|/max(|H1|)"), režģis
diagramma(w./(2*pi),abs(H2)./maks.(abs(H2)),"b")
xlabel("f, Hz"), ylabel("|H2|/max(|H2|)"), režģis
diagramma(w./(2*pi),20*log10(abs(H1)),"r")
title("Zemas caurlaidības FIR filtra ar taisnstūra logu frekvences reakcija, ja N = 15")
xlabel("f, Hz"), ylabel("20lg(|H1|), dB"), režģis
diagramma(w./(2*pi),20*log10(abs(H2)),"b")
title ("Zemas caurlaidības FIR filtra ar taisnstūra logu frekvences reakcija N = 50")
xlabel("f, Hz"), ylabel("20lg(|H2|), dB"), režģis
2. att. Zemas caurlaidības FIR filtra frekvences reakcijas diagrammas ar taisnstūra loga nogriešanas frekvenci filtra garuma vērtībām un lineārā mērogā
3. att. Zemas caurlaidības FIR filtra frekvences reakcijas diagrammas ar taisnstūra loga nogriešanas frekvenci filtra garuma vērtībām un logaritmiskā skalā
Komentārs:
1. tabula. Caurlaides joslas diapazons, pārejas apgabals un apturēšanas josla filtra garumam un
|
Filtra garums |
Joslas platums, Hz |
Pārejas reģions, Hz |
Stopjosla, Hz |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Lekcija Nr.10 "Ciparu filtri ar ierobežotu impulsu reakciju" Fiziski realizējama digitālā galīgā impulsa atbildes filtra (FIR filtra) pārsūtīšanas funkciju var attēlot kā (10.1). Aizstājot izteiksmē (10.1), iegūstam FIR filtra frekvences raksturlielumu formā Kur Fāzes aizkave filtrs ir definēts kā Grupas kavēšanās filtrs ir definēts kā FIR filtru atšķirīga iezīme ir iespēja ieviest pastāvīgu fāzes un grupu aizkavi, t.i. lineārā fāzes reakcija (10.5), kur - nemainīgs. Ja šis nosacījums ir izpildīts, signāls, kas iet caur filtru, neizkropļo tā formu. Lai iegūtu nosacījumus, kas nodrošina lineāru fāzes reakciju, mēs rakstām FIR filtra frekvences reakciju, ņemot vērā (10.5) Pielīdzinot šīs vienlīdzības reālās un iedomātās daļas, mēs iegūstam Dalot otro vienādojumu ar pirmo, mēs iegūstam Beidzot varam rakstīt Šim vienādojumam ir divi risinājumi. Vispirms kad a =0 atbilst vienādojumam Šim vienādojumam ir unikāls risinājums, kas atbilst patvaļīgam h (0) (sin (0) = 0) un h (n) = 0 n >0. Šis risinājums atbilst filtram, kura impulsa reakcijai sākotnējā brīdī ir viens paraugs, kas nav nulle. Šāds filtrs praktiski neinteresē. Mēs atradīsim citu risinājumu. Šajā gadījumā, krusteniski reizinot skaitītājus un saucējus (10.8), mēs iegūstam (10.11). No šejienes mums ir Tā kā šim vienādojumam ir Furjē rindas forma, tā risinājums, ja tāds pastāv, ir unikāls. Ir viegli saprast, ka šī vienādojuma risinājumam ir jāatbilst nosacījumiem (10.13), (10.14). No nosacījuma (10.13.) izriet, ka katrai filtra secībai N ir tikai viena fāzes aizkave a , pie kura var panākt stingru fāzes reakcijas linearitāti. No nosacījuma (10.14.) izriet, ka filtra impulsa reakcijai jābūt simetriskai attiecībā pret nepāra punktu. N , un attiecībā pret intervāla viduspunktu (10.1. att.).
Šāda filtra frekvences reakcija (nepāra gadījumā N ) var rakstīt formā (10.15). Aizstāšanas veikšana otrajā summā m = N -1- n , mēs iegūstam (10.16). Tā kā h (n)= h (N -1- n ), tad abas summas var apvienot Aizstājot, mēs iegūstam (10.18). Ja mēs iecelsim tad beidzot varam rakstīt Tādējādi filtram ar lineāru fāzes reakciju mums ir Gadījumā pat N līdzīgi būs arī mums Veicot aizstāšanu otrajā summā, mēs iegūstam Veicot aizstāšanu, mēs iegūstam (10.24). Norādījis mums beidzot būs Tādējādi FIR filtram ar lineāru fāzes reakciju un vienmērīgu secību N var rakstīt Turpmāk vienkāršības labad mēs aplūkosim tikai filtrus ar nepāra secību. Sintezējot filtra pārsūtīšanas funkciju, sākotnējie parametri, kā likums, ir prasības frekvences reakcijai. FIR filtru sintezēšanai ir daudz paņēmienu. Apskatīsim dažus no tiem. Tā kā jebkura digitālā filtra frekvences reakcija ir periodiska frekvences funkcija, to var attēlot kā Furjē sēriju kur Furjē rindas koeficienti ir vienādi Var redzēt, ka Furjē sērijas koeficienti h(n ) sakrīt ar filtra impulsa reakcijas koeficientiem. Līdz ar to, ja ir zināms filtra nepieciešamās frekvences reakcijas analītiskais apraksts, tad ir iespējams viegli noteikt impulsa reakcijas koeficientus un no tiem filtra pārneses funkciju. Tomēr praksē tas nav iespējams, jo šāda filtra impulsa reakcijai ir bezgalīgs garums. Turklāt šāds filtrs nav fiziski realizējams, jo impulsa reakcija sākas plkst.¥ , un nekāda ierobežota aizkave nepadarīs šo filtru fiziski realizējamu. Viena no iespējamām metodēm FIR filtra iegūšanai, kas tuvina doto frekvences reakciju, ir bezgalīgās Furjē sērijas un filtra impulsa reakcijas saīsināšana, pieņemot, ka h (n)=0 pie . Tad Pārneses funkcijas fiziskā realizējamība H(z ) var panākt, reizinot H(z) ieslēgts . Kur (10.32). Ar šādu pārsūtīšanas funkcijas modifikāciju filtra amplitūdas raksturlielums nemainās, un grupas aizkave palielinās par nemainīgu daudzumu. Piemēram, aprēķināsim zemas caurlaidības FIR filtru ar formas frekvences reakciju Saskaņā ar (10.29) filtra impulsa reakcijas koeficientus apraksta ar izteiksmi Tagad no (10.31) mēs varam iegūt pārsūtīšanas funkcijas izteiksmi Kur (10.36). Aprēķinātā filtra amplitūdas raksturlielumi dažādiem N ir parādīti 10.2. attēlā.
Att.10.2 Pulsācija caurlaides joslā un apturēšanas joslā rodas Furjē sērijas lēnās konverģences dēļ, ko savukārt izraisa funkcijas pārtraukums pie caurlaides joslas nogriešanas frekvences. Šīs pulsācijas ir pazīstamas kā Gibbs viļņojas. No 10.2. att. redzams, ka pieaugot N pulsācijas frekvence palielinās un amplitūda samazinās gan zemākās, gan augstākās frekvencēs. Tomēr pēdējā viļņojuma amplitūda caurlaides joslā un pirmā viļņojuma amplitūda apturēšanas joslā praktiski nemainās. Praksē šādas sekas bieži vien ir nevēlamas, tāpēc ir jāatrod veidi, kā samazināt Gibsa pulsāciju. Saīsināta impulsa reakcija h(n ) var attēlot kā vajadzīgās bezgalīgās impulsa atbildes reizinājumu un dažus logu funkcijas w (n) ar garumu n (10.3. att.).
Aplūkotajā Furjē sērijas vienkāršas saīsināšanas gadījumā mēs izmantojam taisnstūra logs Šajā gadījumā filtra frekvences reakciju var attēlot kā sarežģītu konvolūciju Tas nozīmē, ka tā būs vajadzīgā raksturlieluma "izplūdusi" versija. Problēma ir saistīta ar logu funkciju atrašanu, kas ļauj samazināt Gibsa pulsāciju ar tādu pašu filtra selektivitāti. Lai to izdarītu, vispirms ir jāizpēta loga funkcijas īpašības, izmantojot taisnstūra loga piemēru. Taisnstūra loga funkcijas spektru var uzrakstīt kā Taisnstūra loga funkcijas spektrs parādīts 10.4. attēlā.
Att.10.4 Tā kā pie , spektra galvenās daivas platums izrādās vienāds ar . Sānu daivu klātbūtne loga funkcijas spektrā izraisa Gibsa pulsācijas palielināšanos filtra frekvences atbildē. Lai panāktu zemu viļņošanos caurlaides joslā un augstu vājināšanos bloķēšanas joslā, ir nepieciešams, lai sānu daivu ierobežotā platība būtu neliela daļa no galvenās daivas ierobežotā laukuma. Savukārt galvenās daivas platums nosaka iegūtā filtra pārejas zonas platumu. Lai nodrošinātu augstu filtra selektivitāti, galvenās daivas platumam jābūt pēc iespējas mazākam. Kā redzams no iepriekš minētā, galvenās daivas platums samazinās, palielinoties filtru secībai. Tādējādi piemērotu logu funkciju īpašības var formulēt šādi: - loga funkcijai jābūt ierobežotai laikā; - loga funkcijas spektram vislabāk būtu jāatbilst frekvences ierobežotajai funkcijai, t.i. ir minimāla enerģija ārpus galvenās daivas; - Loga funkciju spektra galvenās daivas platumam jābūt pēc iespējas mazākam. Visbiežāk izmantotās logu funkcijas ir: 1. Taisnstūra logs. Iepriekš apspriests. 2. Izkalšanas logs. Kur. Šo logu sauc par Hannas logu ( hanning). 3. Blackman logs. 4. Bārtleta logs. Izmantojot norādītās loga funkcijas, izveidoto filtru rādītāji ir apkopoti 10.1. tabulā.
Pulsācijas koeficients ir definēts kā sānu daivas maksimālās amplitūdas attiecība pret galvenās daivas amplitūdu loga funkcijas spektrā. Lai izvēlētos nepieciešamo filtru secību un atbilstošāko loga funkciju, aprēķinot reālos filtrus, var izmantot 10.2. tabulas datus.
Kā redzams no 10.1. tabulas, pastāv noteikta sakarība starp pulsācijas koeficientu un galvenās daivas platumu loga funkcijas spektrā. Jo mazāks pulsācijas koeficients, jo lielāks ir galvenās daivas platums un līdz ar to arī pārejas zona filtra frekvences atbildē. Lai nodrošinātu zemu pulsāciju caurlaides joslā, ir jāizvēlas logs ar piemērotu pulsācijas koeficientu un jānodrošina nepieciešamais pārejas zonas platums ar palielinātu filtru secību N. Šo problēmu var atrisināt, izmantojot Kaiser piedāvāto logu. Kaiser loga funkcijai ir forma
kur a ir neatkarīgs parametrs,
Kaiser loga pievilcīga īpašība ir iespēja vienmērīgi mainīt pulsācijas koeficientu no mazām uz lielām vērtībām, vienlaikus mainot tikai vienu parametru a. Šajā gadījumā, tāpat kā citām loga funkcijām, galvenās daivas platumu var regulēt pēc filtra secības N. Galvenie parametri, kas iestatīti, izstrādājot reālu filtru, ir: Joslas platums - w p ; Šķēršļu josla - w a ; Maksimālais pieļaujamais viļņojums caurlaides joslā ir A p ; Minimālais stopjoslas vājinājums – A a ; -paraugu ņemšanas biežums - ws. Šie parametri ir parādīti 10.5. attēlā. Šajā gadījumā maksimālo pulsāciju caurlaides joslā nosaka kā
un minimālais vājinājums stopjoslā ir kā Salīdzinoši vienkāršā procedūra filtra aprēķināšanai ar Kaiser logu ietver šādas darbības: 1. Nosaka filtra h (n) impulsa reakciju, ja frekvences reakcija ir ideāla
kur (10.49). 2. Parametrs d ir izvēlēts kā
Kur 3. A a un A p patieso vērtību aprēķina, izmantojot formulas (10.46), (10.47). 4. Parametrs a ir izvēlēts kā
5. Parametrs D ir izvēlēts kā
6. No nosacījuma atlasiet filtra secības mazāko nepāra vērtību
tam seko Tā kā filtra impulsa reakcijas paraugi ir tā pārneses funkcijas koeficienti, nosacījums (10.59) nozīmē, ka visu filtra koeficientu kodi satur tikai daļdaļu un zīmes bitu un nesatur veselo skaitļu daļu. Filtra koeficientu daļējās daļas ciparu skaits tiek noteikts, ņemot vērā nosacījumu, ka tiek izpildīta filtra pārsūtīšanas funkcija ar kvantētajiem koeficientiem, norādītajām prasībām, lai tuvotos atsauces pārsūtīšanas funkcijai ar precīzām koeficientu vērtībām. Filtra ieejas signāla paraugu absolūtās vērtības parasti tiek normalizētas tā, lai Ja analīze tiek veikta FIR filtram ar lineāru fāzes reakciju, tad tā izejas signāla aprēķināšanas algoritms var būt šāds kur filtra koeficienti noapaļoti līdz s k. Šis algoritms atbilst filtra blokshēmai, kas parādīta 10.5. attēlā.
Ir divi veidi, kā ieviest šo algoritmu. Pirmajā gadījumā visas reizināšanas darbības tiek veiktas precīzi un nenotiek reizinājumu noapaļošana. Šajā gadījumā produktu bitu dziļums ir vienāds ar s in +s k, kur s in ir ievades signāla bitu dziļums, un s k ir filtra koeficientu bitu dziļums. Šajā gadījumā 10.5. attēlā redzamā filtra blokshēma precīzi atbilst reālajam filtram. Otrajā algoritma (10.61) realizācijas metodē katrs reizināšanas darbības rezultāts tiek noapaļots, t.i. produkti tiek aprēķināti ar zināmu kļūdu. Šajā gadījumā ir jāmaina algoritms (10.61), lai ņemtu vērā kļūdu, kas radusies, noapaļojot reizinājumus. Ja filtra izejas signāla izlases vērtības tiek aprēķinātas, izmantojot pirmo metodi (ar precīzām produktu vērtībām), tad izejas trokšņa izkliedi nosaka kā
tie. ir atkarīgs no ieejas signāla noapaļošanas trokšņa dispersijas un filtra koeficientu vērtībām. No šejienes jūs varat atrast nepieciešamo ieejas signāla bitu skaitu kā
Izmantojot zināmās s in un s k vērtības, var noteikt bitu skaitu, kas nepieciešams izejas signāla koda daļējai daļai kā Ja izejas signāla paraugu vērtības aprēķina, izmantojot otro metodi, kad katrs reizinājums ir noapaļots līdz s d cipariem, tad katra reizinātāja radītā noapaļošanas trokšņa izkliedi var izteikt kā ciparu kapacitāti. produkts kā DR ieeja un signāla-trokšņa attiecība pie filtra izejas SNR out. Ieejas signāla dinamiskais diapazons decibelos ir definēts kā
kur A max un A min ir filtra ieejas signāla maksimālā un minimālā amplitūda. Signāla un trokšņa attiecība pie filtra izejas, kas izteikta decibelos, ir definēta kā
nosaka filtra ar amplitūdu A min izejas sinusoidālā signāla jaudas vidējo kvadrātisko vērtību un (10.77) nosaka trokšņa jaudu pie filtra izejas. No (10.75) un (10.76) ar A max =1 iegūstam filtra izejas trokšņa izkliedes izteiksmi Šo filtra izejas trokšņu izkliedes vērtību var izmantot, lai aprēķinātu filtra ieejas un izejas signālu bitu dziļumu.  Bezmaksas programmu un noderīgu padomu pasaule 2024 whatsappss.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(10.2),
- amplitūdas-frekvences reakcija (AFC) filtrs,
- fāzes frekvences reakcija (PFC) filtru.
(10.3).
(10.4).
(10.6).
(10.7).
(10.8).
(10.9).
(10.10).
(10.12).
(10.17).
(10.19),
(10.20).
(10.21).
(10.22).
(10.23).
(10.25),
(10.26).
(10.27).
(10.28),
(10.29).
(10.30).
(10.31),
(10.33).
(10.34).
(10.35),
(10.37).
(10.38).
(10.39).
(10.40).
(10.41),
(10.42).
(10.43).
(10.44),
, I 0 – pirmā veida nulles kārtas Besela funkcija, ko definē izteiksme
(10.45).
(10.46),
(10.50),
(10.51).
(10.52).
(10.53).
(10.54),
(10.57)
(10.66),
(10.67).
(10.74),
(10.75),
(10.78).