Κρουστική απόκριση του φίλτρου. Ψηφιακά φίλτρα με πεπερασμένη παλμική απόκριση. Εξομάλυνση δεδομένων. Μέσο φιλτράρισμα
48 Ψηφιακά φίλτρα με πεπερασμένη απόκριση παλμών. Υπολογισμός φίλτρων kih.
Φίλτρο πεπερασμένης απόκρισης παλμών (Μη αναδρομικό φίλτρο, Φίλτρο FIR) ή φίλτρο FIR (FIR συντομεύεται από την απόκριση πεπερασμένης ώθησης - πεπερασμένη παλμική απόκριση) - ένας από τους τύπους γραμμικών ψηφιακών φίλτρων, χαρακτηριστικό του οποίου είναι ο χρονικός περιορισμός του παρορμητική απόκριση(από κάποιο χρονικό σημείο γίνεται ακριβώς ίσο με το μηδέν). Ένα τέτοιο φίλτρο ονομάζεται επίσης μη αναδρομικό λόγω της έλλειψης ανάδρασης. Ο παρονομαστής της συνάρτησης μεταφοράς ενός τέτοιου φίλτρου είναι μια ορισμένη σταθερά.
Εξίσωση διαφοράς που περιγράφει τη σχέση μεταξύ των σημάτων εισόδου και εξόδου του φίλτρου: όπου Π- παραγγελία φίλτρου, Χ(n) - σήμα εισόδου, y(n) είναι το σήμα εξόδου και σι Εγώ- συντελεστές φίλτρου. Με άλλα λόγια, η τιμή οποιουδήποτε δείγματος σήματος εξόδου προσδιορίζεται από το άθροισμα των κλιμακωμένων τιμών Ππροηγούμενες αναγνώσεις. Μπορείτε να το πείτε διαφορετικά: η τιμή της εξόδου του φίλτρου ανά πάσα στιγμή είναι η τιμή της απόκρισης στη στιγμιαία τιμή της εισόδου και το άθροισμα όλων των αποκρίσεων που σταδιακά αποσυντίθενται Ππροηγούμενα δείγματα σήματος που εξακολουθούν να επηρεάζουν την έξοδο (μετά Π-μετράει, η συνάρτηση μετάβασης παλμού γίνεται ίση με μηδέν, όπως ήδη αναφέρθηκε, επομένως όλοι οι όροι μετά Π-ο θα γίνει επίσης ίσο με μηδέν). Ας γράψουμε την προηγούμενη εξίσωση με μια πιο ευρεία μορφή:
Για να βρούμε τον πυρήνα του φίλτρου βάζουμε
Χ(n) = δ( n)
όπου δ( n) - συνάρτηση δέλτα. Τότε η κρουστική απόκριση του φίλτρου FIR μπορεί να γραφτεί ως:
Ο μετασχηματισμός Z της παλμικής απόκρισης μας δίνει τη συνάρτηση μεταφοράς του φίλτρου FIR:
]Ιδιότητες
Το φίλτρο FIR έχει μια σειρά από χρήσιμες ιδιότητες που το κάνουν μερικές φορές προτιμότερο να χρησιμοποιείται από ένα φίλτρο IIR. Εδώ είναι μερικά από αυτά:
Τα φίλτρα FIR είναι στιβαρά.
Τα φίλτρα FIR δεν απαιτούν ανάδραση όταν εφαρμόζονται.
Η φάση των φίλτρων FIR μπορεί να γίνει γραμμική
Άμεση μορφή φίλτρου FIR
Τα φίλτρα FIR μπορούν να εφαρμοστούν χρησιμοποιώντας τρία στοιχεία: έναν πολλαπλασιαστή, έναν αθροιστή και ένα μπλοκ καθυστέρησης. Η επιλογή που φαίνεται στο σχήμα είναι μια άμεση εφαρμογή των φίλτρων FIR τύπου 1.
Υλοποίηση της άμεσης μορφής του φίλτρου FIR
Παράδειγμα προγράμματος
Παρακάτω είναι ένα παράδειγμα προγράμματος φίλτρου FIR γραμμένο σε C:
/* Φίλτρο FIR για 128 πατήματα */
float fir_filter (είσοδος float)
δείγμα στατικού πλωτήρα.
acc = 0,0f; /* Μπαταρία */
/* Πολλαπλασιασμός και συσσώρευση */
για (i = 0; i< 128; i++) {
acc += (h[i] * δείγμα[i]);
/* Έξοδος */
/* Μετατόπιση του καθυστερημένου σήματος */
για (i = 127; i > 0; i--)
δείγμα[i] = δείγμα;
49 Εξομάλυνση δεδομένων. Μετακίνηση κατά μέσο όρο.
50 Εξομάλυνση δεδομένων. Παραβολική εξομάλυνση.
51 Εξομάλυνση δεδομένων. Spencer εξομάλυνση.
52 Εξομάλυνση δεδομένων. Μέσο φιλτράρισμα.
Κινούμενος μέσος όρος, παραβολική εξομάλυνση, εξομάλυνση Spencer, διάμεσος φιλτράρισμα
Κατά την ανάπτυξη μεθόδων για τον προσδιορισμό των παραμέτρων των φυσικών διεργασιών που αλλάζουν αργά με την πάροδο του χρόνου, ένα σημαντικό καθήκον είναι η εξάλειψη της επίδρασης των φαινομένων θορύβου ή των τυχαίων παρεμβολών που υπερτίθενται στο επεξεργασμένο σήμα που λαμβάνεται στην έξοδο του πρωτεύοντος μετατροπέα.
Για να εξαλείψετε αυτό το αποτέλεσμα, μπορείτε να εφαρμόσετε εξομάλυνση δεδομένων. Μία από τις απλούστερες μεθόδους τέτοιας εξομάλυνσης είναι ο αριθμητικός μέσος όρος. Όταν χρησιμοποιείται, κάθε τιμή μιας διακριτής συνάρτησης (πίνακας επεξεργασμένων δεδομένων) υπολογίζεται σύμφωνα με την έκφραση:
πού είναι ο αριθμός των σημείων για τον αριθμητικό μέσο όρο (μονός ακέραιος);
Η τιμή της συνάρτησης πριν από την επεξεργασία.
Υπάρχουν και άλλες αρκετά αποτελεσματικές μέθοδοι εξομάλυνσης, για παράδειγμα, με παραβολές δεύτερου βαθμού σε πέντε, επτά, εννέα και έντεκα σημεία σύμφωνα με τις εκφράσεις:
ή παραβολές τέταρτου βαθμού σε επτά, εννέα, έντεκα και δεκατρία σημεία:
Σε πρακτικές εφαρμογές, άλλες αποτελεσματικές μέθοδοι, για παράδειγμα η εξομάλυνση Spencer 15 σημείων, δίνουν καλά αποτελέσματα:
Αντικαθιστώντας τη μιγαδική εκθετική , όπου σε αυτές τις εκφράσεις, μπορούμε να προσδιορίσουμε τη συνάρτηση μεταφοράς του αντίστοιχου μετασχηματισμού.
Για τον αριθμητικό μέσο όρο
Η έκφραση σε παρένθεση αντιπροσωπεύει μια γεωμετρική πρόοδο με παρονομαστή, επομένως αυτή η έκφραση μπορεί να αναπαρασταθεί ως:
.
Αυτός ο τύπος αντιπροσωπεύει το χαρακτηριστικό μεταφοράς ενός χαμηλοπερατού φίλτρου και δείχνει ότι όσο περισσότεροι όροι εμπλέκονται στον μέσο όρο, τόσο μεγαλύτερη είναι η καταστολή των στοιχείων θορύβου υψηλής συχνότητας στο σήμα (βλ. Εικόνα 6.1).
Ωστόσο, η σημασιολογική έννοια της συχνότητας κατά την επεξεργασία των τάσεων του χρόνου διαφέρει από μια παρόμοια έννοια κατά την επεξεργασία σημάτων. Αυτό εξηγείται από το γεγονός ότι κατά τη μελέτη των τάσεων του χρόνου, δεν ενδιαφέρει η σύνθεση της συχνότητάς τους, αλλά το είδος της αλλαγής (αύξηση, μείωση, σταθερότητα, κυκλικότητα κ.λπ.).
Η χρήση των λεγόμενων ευρετικών αλγορίθμων είναι επίσης αρκετά αποτελεσματική για την εξομάλυνση των δεδομένων.
Ένα από αυτά είναι το μέσο φιλτράρισμα. Κατά την υλοποίησή του σε ένα συρόμενο χρονικό παράθυρο διάστασης , όπου ο ακέραιος αριθμός είναι περιττός αριθμός, το κεντρικό στοιχείο αντικαθίσταται από το μεσαίο στοιχείο της ακολουθίας, τα οποία ταξινομούνται, κατά αύξουσα σειρά τιμών, στοιχεία του πίνακα δεδομένων του εξομαλυνθέντος σήμα που εμπίπτει εντός του χρονικού παραθύρου. Το πλεονέκτημα του μέσου φιλτραρίσματος είναι η δυνατότητα αφαίρεσης παλμικού θορύβου, η διάρκεια του οποίου δεν υπερβαίνει, χωρίς ουσιαστικά καμία παραμόρφωση των ομαλά μεταβαλλόμενων σημάτων. Αυτή η μέθοδος καταστολής θορύβου δεν έχει αυστηρή μαθηματική αιτιολόγηση, αλλά η απλότητα των υπολογισμών και η αποτελεσματικότητα των αποτελεσμάτων που προέκυψαν έχουν οδηγήσει στην ευρεία χρήση της.
Εικόνα 6.1 - Μεταφορά χαρακτηριστικών γραφημάτων
Πράξεις υπολογισμού μέσου όρου για m=5, 7, 9, 11
Ένας άλλος ενδιαφέρον αλγόριθμος εξομάλυνσης είναι ο μέσος όρος. Η ουσία του είναι η εξής. Σε ένα συρόμενο χρονικό παράθυρο μεγέθους (-μονός ακέραιος), τα στοιχεία του πίνακα δεδομένων ταξινομούνται με αύξουσα σειρά και, στη συνέχεια, το πρώτο και το τελευταίο στοιχείο αφαιρούνται από τη διατεταγμένη ακολουθία (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
Αυτή η μέθοδος σάς επιτρέπει να καταστείλετε τις παρεμβολές παλμών και ραδιοσυχνοτήτων, καθώς και να επιτύχετε καλή εξομάλυνση του σήματος.
| " |
Ας εξετάσουμε τα πιο απλά από τα ψηφιακά φίλτρα - φίλτρα με σταθερές παραμέτρους.
Το σήμα εισόδου του ψηφιακού φίλτρου παρέχεται με τη μορφή μιας ακολουθίας αριθμητικών τιμών, που ακολουθούν κατά διαστήματα (Εικ. 4.1, α). Όταν λαμβάνεται κάθε επόμενη τιμή σήματος στο ψηφιακό φίλτρο, υπολογίζεται η επόμενη τιμή του σήματος εξόδου.Οι αλγόριθμοι υπολογισμού μπορεί να είναι πολύ διαφορετικοί. κατά τη διαδικασία υπολογισμού, εκτός από την τελευταία τιμή του σήματος εισόδου, μπορεί να χρησιμοποιηθεί
προηγούμενες τιμές των σημάτων εισόδου και εξόδου: Το σήμα εξόδου ενός ψηφιακού φίλτρου είναι επίσης μια ακολουθία αριθμητικών τιμών μετά από ένα διάστημα . Αυτό το διάστημα είναι το ίδιο για ολόκληρη τη συσκευή επεξεργασίας ψηφιακού σήματος.
Ρύζι. 4.1. Σήμα στην είσοδο και στην έξοδο του ψηφιακού φίλτρου
Επομένως, εάν εφαρμόσετε το απλούστερο σήμα με τη μορφή ενός μόνο παλμού στην είσοδο ενός ψηφιακού φίλτρου (Εικ. 4.2, α)
τότε στην έξοδο παίρνουμε ένα σήμα με τη μορφή μιας διακριτής ακολουθίας αριθμητικών τιμών, ακολουθώντας ανά διαστήματα
Κατ' αναλογία με τα συμβατικά αναλογικά κυκλώματα, θα ονομάσουμε αυτό το σήμα απόκρισης παλμική απόκριση του φίλτρου (Εικ. 4.2, β). Σε αντίθεση με την κρουστική απόκριση ενός αναλογικού κυκλώματος, η συνάρτηση είναι αδιάστατη.
Ρύζι. 4.2. Μοναδιαία παλμική και παλμική απόκριση ψηφιακού φίλτρου
Ας εφαρμόσουμε ένα αυθαίρετο διακριτό σήμα στην είσοδο του φίλτρου (Εικ. 4.1, α), το οποίο είναι ένα σύνολο διακριτών τιμών
Κάτω από την ενέργεια του πρώτου στοιχείου, σχηματίζεται μια ακολουθία πολλαπλασιαζόμενη επί στην έξοδο του φίλτρου· κάτω από την ενέργεια, μια ακολουθία πολλαπλασιάζεται και μετατοπίζεται προς τα δεξιά κατά ένα ποσό, κ.λπ. Ως αποτέλεσμα, η έξοδος θα λάβει το ακολουθία όπου
Έτσι, το σήμα εξόδου ορίζεται ως η διακριτή συνέλιξη του σήματος εισόδου και η απόκριση παλμού. Από αυτή την άποψη, τα ψηφιακά φίλτρα είναι παρόμοια με τα συμβατικά κυκλώματα, όπου το σήμα εξόδου είναι ίσο με τη συνέλιξη του σήματος εισόδου και την απόκριση παλμού.
Ο τύπος (4.1) είναι ένας ψηφιακός αλγόριθμος φιλτραρίσματος. Εάν η παλμική απόκριση ενός φίλτρου περιγράφεται από μια ακολουθία με πεπερασμένο αριθμό όρων, τότε το φίλτρο μπορεί να υλοποιηθεί με τη μορφή ενός κυκλώματος που φαίνεται στο Σχ. 4.3. Εδώ το γράμμα υποδεικνύει τα στοιχεία της καθυστέρησης σήματος για το χρόνο (ανά κελί). -στοιχεία που πολλαπλασιάζουν το σήμα με τον αντίστοιχο συντελεστή.
Το διάγραμμα που φαίνεται στο Σχ. 4.3 δεν είναι ηλεκτρικό κύκλωμα ψηφιακού φίλτρου. Αυτό το διάγραμμα είναι μια γραφική αναπαράσταση του αλγόριθμου ψηφιακού φιλτραρίσματος και δείχνει την ακολουθία των αριθμητικών πράξεων που εκτελούνται κατά την επεξεργασία του σήματος.
Ρύζι. 4.3. Μη αναδρομικό ψηφιακό κύκλωμα φίλτρου
Για τα ψηφιακά φίλτρα που επεξεργάζονται σήματα με τη μορφή αφηρημένων αριθμητικών ακολουθιών, η έννοια της «χρονοκαθυστέρησης» δεν είναι απολύτως σωστή. Επομένως, στοιχεία που καθυστερούν το σήμα κατά ένα κελί συνήθως επισημαίνονται σε ψηφιακά κυκλώματα φίλτρων με ένα σύμβολο που υποδεικνύει την καθυστέρηση του σήματος στη γλώσσα των -μετασχηματισμών. Σε όσα ακολουθούν θα τηρήσουμε αυτή τη σημειογραφία.
Ας επιστρέψουμε στο ψηφιακό κύκλωμα φίλτρου που φαίνεται στο Σχ. 4.3, Τέτοια φίλτρα, όπου χρησιμοποιούνται μόνο οι τιμές του σήματος εισόδου για υπολογισμό, ονομάζονται απλά ή μη επαναλαμβανόμενα.
Ο αλγόριθμος του μη αναδρομικού φίλτρου είναι εύκολο να γραφτεί εάν είναι γνωστή η κρουστική απόκριση του φίλτρου. Για την πρακτική εφαρμογή του αλγορίθμου, είναι απαραίτητο η παλμική απόκριση να περιέχει έναν πεπερασμένο αριθμό όρων. Εάν η απόκριση ώθησης περιέχει άπειρο αριθμό όρων, αλλά μειώνονται γρήγορα σε αξία, τότε μπορείτε να περιοριστείτε σε έναν πεπερασμένο αριθμό όρων, απορρίπτοντας αυτούς των οποίων οι τιμές είναι μικρές. Εάν τα στοιχεία της παλμικής απόκρισης δεν μειωθούν σε τιμή, ο αλγόριθμος του μη αναδρομικού φίλτρου αποδεικνύεται μη πραγματοποιήσιμος.
Ρύζι. 4.4. -αλυσίδα
Ως παράδειγμα, θεωρήστε το απλούστερο ψηφιακό φίλτρο, παρόμοιο με το -κύκλωμα (Εικ. 4.4). Η κρουστική απόκριση του κυκλώματος έχει τη μορφή
Για να γράψετε την παλμική απόκριση του αντίστοιχου ψηφιακού φίλτρου, η έκφραση θα πρέπει να αντικατασταθεί από την έκφραση Ωστόσο, η κρουστική απόκριση ενός κυκλώματος έχει μια διάσταση και η κρουστική απόκριση ενός ψηφιακού φίλτρου πρέπει να είναι αδιάστατη. Επομένως, παραλείπουμε τον πολλαπλασιαστή στην έκφραση (4.2) και γράφουμε την παλμική απόκριση του ψηφιακού φίλτρου στη μορφή
Μια τέτοια απόκριση ώθησης περιέχει άπειρους όρους, αλλά το μέγεθός τους μειώνεται σύμφωνα με έναν εκθετικό νόμο, και μπορούμε να περιοριστούμε σε όρους, επιλέγοντας τέτοιους
Τώρα μπορούμε να γράψουμε την έκφραση για το σήμα στην έξοδο του φίλτρου
Αυτή η έκφραση είναι επίσης ένας αλγόριθμος ψηφιακού φίλτρου. Το διάγραμμα αυτού του φίλτρου φαίνεται στο Σχ. 4.5.
Η δεύτερη προσέγγιση για την ανάλυση διεργασιών σε ψηφιακά φίλτρα είναι παρόμοια με τη μέθοδο χειριστή για την ανάλυση των συμβατικών αναλογικών κυκλωμάτων, μόνο που αντί του μετασχηματισμού Laplace χρησιμοποιείται ο μετασχηματισμός.
Ρύζι. 4.5. Κύκλωμα ενός μη αναδρομικού ψηφιακού φίλτρου παρόμοιου με ένα -κύκλωμα
Ας ορίσουμε μια παράμετρο ψηφιακού φίλτρου παρόμοια με τη συνάρτηση μεταφοράς ενός ηλεκτρικού κυκλώματος. Για να το κάνετε αυτό, εφαρμόστε έναν μετασχηματισμό στην παλμική απόκριση ενός ψηφιακού φίλτρου:
Η συνάρτηση ονομάζεται συνάρτηση φίλτρου συστήματος.
Σύμφωνα με την έκφραση (4.1), το σήμα στην έξοδο του ψηφιακού φίλτρου είναι ίσο με τη διακριτή περιέλιξη του σήματος εισόδου και την κρουστική απόκριση του φίλτρου. Εφαρμόζοντας το θεώρημα συνέλιξης σε αυτήν την έκφραση, λαμβάνουμε ότι ο μετασχηματισμός του σήματος εξόδου είναι ίσος με τον μετασχηματισμό του σήματος εισόδου πολλαπλασιαζόμενος με τη συνάρτηση φίλτρου συστήματος:
Έτσι, η λειτουργία συστήματος παίζει το ρόλο της συνάρτησης μεταφοράς ενός ψηφιακού φίλτρου.
Για παράδειγμα, ας βρούμε τη λειτουργία συστήματος ενός ψηφιακού φίλτρου πρώτης τάξης παρόμοιου με ένα -κύκλωμα:
Η τρίτη μέθοδος ανάλυσης της διέλευσης σημάτων μέσω ψηφιακών φίλτρων είναι παρόμοια με την κλασική μέθοδο των διαφορικών εξισώσεων. Ας εξετάσουμε αυτή τη μέθοδο χρησιμοποιώντας αλυσίδες παραγγελιών ως παράδειγμα.
Το απλούστερο αναλογικό κύκλωμα 1ης τάξης είναι το -κύκλωμα (βλ. Εικ. 4.4), η διέλευση των σημάτων μέσω του οποίου περιγράφεται από τη διαφορική εξίσωση
Για ένα διακριτό κύκλωμα, αντί για τη διαφορική εξίσωση (4.8), θα πρέπει να γραφεί μια εξίσωση διαφοράς, όπου τα σήματα εισόδου και εξόδου καθορίζονται για διακριτές χρονικές στιγμές και αντί για την παράγωγο, η διαφορά των παρακείμενων τιμών σήματος εμφανίζομαι. Για ένα διακριτό κύκλωμα 1ης τάξης, η εξίσωση διαφοράς μπορεί να γραφτεί σε μια αρκετά γενική μορφή
Ας εφαρμόσουμε τον μετασχηματισμό στην εξίσωση
όπου βρίσκουμε τη λειτουργία φίλτρου συστήματος
Ο τύπος (4.10) είναι μια αρκετά γενική έκφραση για τη λειτουργία συστήματος ενός ψηφιακού φίλτρου 1ης τάξης. Όταν συμπίπτει με την προηγουμένως ληφθείσα έκφραση (4.7) για τη λειτουργία συστήματος ενός ψηφιακού φίλτρου ισοδύναμου με -κύκλωμα.
Ας βρούμε έναν αλγόριθμο ψηφιακού φιλτραρίσματος που αντιστοιχεί στη συνάρτηση συστήματος (4.10). Για να γίνει αυτό, λύνουμε την εξίσωση (4.9) για
Ένα ισοδύναμο διάγραμμα αυτού του αλγορίθμου φαίνεται στο Σχ. 4.6. Σε σύγκριση με ένα μη αναδρομικό φίλτρο (βλ. Εικ. 4.5), έχει προστεθεί εδώ ένα είδος "κυκλώματος ανάδρασης", που σημαίνει ότι οι τιμές του σήματος εξόδου χρησιμοποιούνται στη συνέχεια
Ρύζι. 4.6. Κύκλωμα ενός αναδρομικού ψηφιακού φίλτρου παρόμοιου με ένα -κύκλωμα
υπολογισμούς. Τα φίλτρα αυτού του τύπου ονομάζονται αναδρομικά.
Ο αλγόριθμος (4.11) αντιστοιχεί σε ένα φίλτρο που είναι απολύτως ισοδύναμο με το μη αναδρομικό φίλτρο που εξετάστηκε προηγουμένως. Αλλά για να προσδιορίσετε μια τιμή του σήματος εξόδου χρησιμοποιώντας τον αλγόριθμο μη αναδρομικού φίλτρου (4.4), είναι απαραίτητο να εκτελέσετε λειτουργίες και όταν χρησιμοποιείτε τον αλγόριθμο αναδρομικού φίλτρου (4.11), απαιτούνται μόνο δύο λειτουργίες. Αυτό είναι το κύριο πλεονέκτημα των αναδρομικών φίλτρων. Επιπλέον, τα αναδρομικά φίλτρα επιτρέπουν την επεξεργασία του σήματος με μεγαλύτερη ακρίβεια, καθώς επιτρέπουν την πιο σωστή εφαρμογή της παλμικής απόκρισης χωρίς να απορρίπτεται η «ουρά» της. Τα αναδρομικά φίλτρα σάς επιτρέπουν να εφαρμόσετε αλγόριθμους που δεν μπορούν να εφαρμοστούν καθόλου χρησιμοποιώντας μη αναδρομικά φίλτρα. Για παράδειγμα, με ένα φίλτρο που λειτουργεί σύμφωνα με το κύκλωμα στο Σχ. 4.6, είναι ουσιαστικά ένας ιδανικός συσσωρευτής-ολοκληρωτής και έχει μια παλμική απόκριση της μορφής Ένα φίλτρο με ένα τέτοιο χαρακτηριστικό δεν μπορεί να υλοποιηθεί χρησιμοποιώντας ένα μη αναδρομικό σχήμα.
Τα εξεταζόμενα παραδείγματα δείχνουν ότι δεν έχει νόημα η χρήση μη αναδρομικών αλγορίθμων για τη δημιουργία ψηφιακών φίλτρων με μεγάλη απόκριση παλμών. Σε αυτές τις περιπτώσεις, είναι καταλληλότερο να χρησιμοποιείτε αναδρομικά φίλτρα.
Η περιοχή εφαρμογής των μη αναδρομικών αλγορίθμων είναι η υλοποίηση ψηφιακών φίλτρων με απόκριση παλμού που περιέχει μικρό αριθμό όρων. Ένα παράδειγμα είναι ο απλούστερος διαφοριστής, το σήμα εξόδου του οποίου είναι ίσο με την αύξηση του σήματος εισόδου:
Το κύκλωμα ενός τέτοιου ψηφιακού φίλτρου φαίνεται στο Σχ. 4.7.
Ρύζι. 4.7. Κύκλωμα του απλούστερου ψηφιακού διαφοροποιητή
Ας εξετάσουμε τώρα ένα γενικό ψηφιακό φίλτρο, το οποίο περιγράφεται από την εξίσωση
Αυτή η εξίσωση μπορεί να θεωρηθεί τόσο ως εξίσωση διαφοράς τάξης όσο και ως αλγόριθμος ψηφιακού φιλτραρίσματος, εάν ξαναγραφτεί διαφορετικά, δηλαδή
Ρύζι. 4.8. Αναδρομικό κύκλωμα φίλτρου ψηφιακής παραγγελίας
Ο αλγόριθμος (4.13) αντιστοιχεί στο κύκλωμα που φαίνεται στο Σχ. 4.8. Ας βρούμε τη λειτουργία συστήματος ενός τέτοιου φίλτρου. Για να το κάνετε αυτό, εφαρμόστε τον μετασχηματισμό στην εξίσωση:
Η έκφραση (4.14) μας επιτρέπει να δημιουργήσουμε μια σύνδεση μεταξύ των διακυμάνσεων των στοιχείων του κυκλώματος φίλτρου και της λειτουργίας του συστήματος. Οι συντελεστές στον αριθμητή της συνάρτησης συστήματος καθορίζουν τις τιμές των συντελεστών για
(στο μη αναδρομικό τμήμα του φίλτρου), και οι συντελεστές στον παρονομαστή καθορίζουν το αναδρομικό τμήμα του φίλτρου.
Όλα ξεκίνησαν όταν ένας φίλος ενός φίλου ενός φίλου χρειάστηκε βοήθεια με αυτά τα ίδια φίλτρα. Μέσω των τρόπων των Τζεντάι, φήμες για αυτό έφτασαν σε μένα, απεγγράφηκα στα σχόλια της ανάρτησης στον σύνδεσμο. Φαινόταν να βοηθάει. Λοιπόν, ελπίζω.
Αυτή η ιστορία ξεσήκωσε μέσα μου αναμνήσεις από το τρίτο, ή κάτι σαν, φυσικά, όταν ο ίδιος πήρα το DSP και με ώθησε να γράψω ένα άρθρο για όλους όσους ενδιαφέρονται για το πώς λειτουργούν τα ψηφιακά φίλτρα, αλλά που φυσικά φοβούνται -οι κορυφαίες φόρμουλες και ψυχεδελικές ζωγραφιές σε (ήδη δεν μιλάω για σχολικά βιβλία).
Γενικά, από την εμπειρία μου, η κατάσταση με τα σχολικά βιβλία περιγράφεται από τη γνωστή φράση ότι μερικές φορές δεν μπορείς να δεις το δάσος για τα δέντρα. Και, δηλαδή, όταν αρχίζουν αμέσως να σε τρομάζουν με τον μετασχηματισμό Z και τους τύπους διαίρεσης πολυωνύμων, που συχνά είναι μεγαλύτεροι από δύο πίνακες, το ενδιαφέρον για το θέμα σβήνει εξαιρετικά γρήγορα. Θα ξεκινήσουμε με ένα απλό· ευτυχώς, για να καταλάβουμε τι συμβαίνει, δεν είναι καθόλου απαραίτητο να περιγράψουμε μεγάλες σύνθετες εκφράσεις.
Λοιπόν, πρώτα, μερικές απλές βασικές έννοιες.
1. Παρορμητική απόκριση.
Ας πούμε ότι έχουμε ένα κουτί με τέσσερις καρφίτσες. Δεν έχουμε ιδέα τι υπάρχει μέσα, αλλά γνωρίζουμε με βεβαιότητα ότι οι δύο αριστεροί τερματικοί σταθμοί είναι η είσοδος και οι δύο δεξιοί είναι η έξοδος. Ας προσπαθήσουμε να εφαρμόσουμε έναν πολύ σύντομο παλμό πολύ μεγάλου πλάτους σε αυτό και να δούμε τι συμβαίνει στην έξοδο. Λοιπόν, δεν είναι ξεκάθαρο τι υπάρχει μέσα σε αυτό το τετράπολο, γιατί δεν είναι σαφές πώς να το περιγράψουμε, αλλά τουλάχιστον θα δούμε κάτι.
Εδώ πρέπει να ειπωθεί ότι ένας σύντομος (γενικά μιλώντας, απείρως σύντομος) παλμός μεγάλου (γενικά μιλώντας, άπειρο) πλάτος στη θεωρία ονομάζεται συνάρτηση δέλτα. Παρεμπιπτόντως, το αστείο είναι ότι το αναπόσπαστο αυτό ατελείωτεςη συνάρτηση είναι ίση με ένα. Αυτή είναι η ομαλοποίηση.
Έτσι, αυτό που είδαμε στην έξοδο του τετραπολικού δικτύου, έχοντας εφαρμόσει τη συνάρτηση δέλτα στην είσοδο, ονομάζεται παρορμητική απόκρισηαυτό το τετράπολο. Προς το παρόν, ωστόσο, δεν είναι ξεκάθαρο πώς θα μας βοηθήσει, αλλά ας θυμηθούμε το αποτέλεσμα και ας προχωρήσουμε στην επόμενη ενδιαφέρουσα ιδέα.
2. Συνέλιξη.
Εν ολίγοις, η συνέλιξη είναι μια μαθηματική πράξη που καταλήγει στην ολοκλήρωση του γινομένου των συναρτήσεων:
Όπως μπορείτε να δείτε, υποδεικνύεται με έναν αστερίσκο. Μπορείτε επίσης να δείτε ότι κατά τη συνέλιξη, μια συνάρτηση λαμβάνεται με τη σειρά "εμπρός" και περνάμε από τη δεύτερη "πίσω προς τα εμπρός". Φυσικά, στη διακριτή περίπτωση, που είναι πιο πολύτιμη για την ανθρωπότητα, η συνέλιξη, όπως κάθε αναπόσπαστο, πηγαίνει στην άθροιση:
Θα φαινόταν σαν κάποιο είδος βαρετής μαθηματικής αφαίρεσης. Ωστόσο, στην πραγματικότητα, μια δέσμη είναι ίσως το πιο μαγικό φαινόμενο αυτού του κόσμου, δεύτερο μόνο σε εκπληκτική γέννηση μετά τη γέννηση ενός ατόμου, με τη μόνη διαφορά ότι οι περισσότεροι άνθρωποι ανακαλύπτουν από πού προέρχονται τα παιδιά τουλάχιστον μέχρι την ηλικία των δεκαοκτώ, ενώ για το Τι είναι η συνέλιξη και γιατί είναι χρήσιμη και εκπληκτική, ένα τεράστιο μέρος του πληθυσμού της Γης δεν έχει καμία απολύτως ιδέα για όλη του τη ζωή.
Έτσι, η ισχύς αυτής της λειτουργίας έγκειται στο γεγονός ότι εάν f είναι οποιοδήποτε αυθαίρετο σήμα εισόδου και g είναι η κρουστική απόκριση ενός δικτύου τεσσάρων θυρών, τότε το αποτέλεσμα της συνέλιξης αυτών των δύο συναρτήσεων θα είναι παρόμοιο με αυτό που θα κάναμε λάβετε περνώντας το σήμα f μέσω αυτού του δικτύου τεσσάρων θυρών.
Δηλαδή, η παλμική απόκριση είναι ένα πλήρες cast όλων των ιδιοτήτων του δικτύου τεσσάρων θυρών σε σχέση με το εφέ εισόδου και η συνέλιξη του σήματος εισόδου με αυτό σας επιτρέπει να επαναφέρετε το αντίστοιχο σήμα εξόδου. Κατά τη γνώμη μου, αυτό είναι απλά εκπληκτικό!
3. Φίλτρα.
Μπορείτε να κάνετε πολλά ενδιαφέροντα πράγματα με παρορμητική απόκριση και συνέλιξη. Για παράδειγμα, εάν το σήμα είναι ηχητικό, μπορείτε να οργανώσετε αντήχηση, ηχώ, ρεφρέν, flanger και πολλά, πολλά άλλα. μπορείς να διαφοροποιήσεις και να ενσωματώσεις... Γενικά, μπορείς να δημιουργήσεις οτιδήποτε. Για εμάς τώρα, το πιο σημαντικό είναι ότι, φυσικά, τα φίλτρα μπορούν επίσης να ληφθούν εύκολα χρησιμοποιώντας τη συνέλιξη.
Το ίδιο το ψηφιακό φίλτρο είναι η περιέλιξη του σήματος εισόδου με μια παλμική απόκριση που αντιστοιχεί στο επιθυμητό φίλτρο.
Αλλά, φυσικά, η παρόρμηση πρέπει να επιτευχθεί με κάποιο τρόπο. Φυσικά, έχουμε ήδη καταλάβει πώς να το μετρήσουμε παραπάνω, αλλά σε μια τέτοια εργασία δεν έχει νόημα - αν έχουμε ήδη συναρμολογήσει το φίλτρο, γιατί να μετρήσουμε οτιδήποτε άλλο, μπορούμε να το χρησιμοποιήσουμε ως έχει. Και, επιπλέον, η πιο σημαντική αξία των ψηφιακών φίλτρων είναι ότι μπορούν να έχουν χαρακτηριστικά που είναι ανέφικτα (ή πολύ δύσκολο να επιτευχθούν) στην πραγματικότητα - για παράδειγμα, γραμμική φάση. Οπότε δεν υπάρχει κανένας τρόπος μέτρησης εδώ, απλά πρέπει να μετρήσετε.
4. Λήψη παρορμητικής απόκρισης.
Σε αυτό το σημείο, στις περισσότερες δημοσιεύσεις σχετικά με το θέμα, οι συγγραφείς αρχίζουν να ρίχνουν βουνά από μετασχηματισμούς Z και κλάσματα από πολυώνυμα στον αναγνώστη, μπερδεύοντάς τον εντελώς. Δεν θα το κάνω αυτό, απλώς θα εξηγήσω εν συντομία τι είναι όλο αυτό και γιατί στην πράξη δεν είναι πολύ απαραίτητο για το προοδευτικό κοινό.
Ας πούμε ότι αποφασίσαμε τι θέλουμε από ένα φίλτρο και δημιουργήσαμε μια εξίσωση που το περιγράφει. Στη συνέχεια, για να βρείτε την απόκριση παλμού, μπορείτε να αντικαταστήσετε τη συνάρτηση δέλτα στην εξίσωση που προκύπτει και να πάρετε την επιθυμητή. Το μόνο πρόβλημα είναι πώς να το κάνετε αυτό, επειδή η συνάρτηση δέλτα είναι εγκαίρως ΟΗ περιοχή δίνεται από ένα πονηρό σύστημα, και γενικά υπάρχουν όλα τα άπειρα. Σε αυτή τη φάση λοιπόν όλα αποδεικνύονται τρομερά δύσκολα.
Εδώ συμβαίνει να θυμούνται ότι υπάρχει κάτι όπως ο μετασχηματισμός Laplace. Από μόνο του δεν είναι ούτε κιλό σταφίδες. Ο μόνος λόγος που γίνεται ανεκτός στη ραδιομηχανική είναι ακριβώς το γεγονός ότι στον χώρο του επιχειρήματος στο οποίο αυτός ο μετασχηματισμός αποτελεί μετάβαση, κάποια πράγματα στην πραγματικότητα γίνονται πιο απλά. Συγκεκριμένα, η ίδια συνάρτηση δέλτα που μας δημιούργησε τόσο προβλήματα στον τομέα του χρόνου εκφράζεται πολύ εύκολα - εδώ είναι μόνο μία!
Ο μετασχηματισμός Z (γνωστός και ως μετασχηματισμός Laurent) είναι μια έκδοση του μετασχηματισμού Laplace για διακριτά συστήματα.
Δηλαδή, εφαρμόζοντας τον μετασχηματισμό Laplace (ή τον μετασχηματισμό Z, ανάλογα με τις ανάγκες) στη συνάρτηση που περιγράφει το επιθυμητό φίλτρο, αντικαθιστώντας ένα με το προκύπτον και μετασχηματίζοντας ξανά, λαμβάνουμε την απόκριση παλμού. Ακούγεται εύκολο, ο καθένας μπορεί να το δοκιμάσει. Δεν θα το ρισκάρω, γιατί, όπως ήδη αναφέρθηκε, ο μετασχηματισμός Laplace είναι σκληρό πράγμα, ειδικά το αντίστροφο. Ας το αφήσουμε ως έσχατη λύση και θα αναζητήσουμε μερικούς απλούστερους τρόπους για να αποκτήσουμε αυτό που ψάχνουμε. Υπάρχουν αρκετά από αυτά.
Πρώτον, μπορούμε να θυμηθούμε ένα άλλο εκπληκτικό γεγονός της φύσης - τα χαρακτηριστικά πλάτους-συχνότητας και παλμών σχετίζονται μεταξύ τους από τον καλό και οικείο μετασχηματισμό Fourier. Αυτό σημαίνει ότι μπορούμε να σχεδιάσουμε οποιαδήποτε απόκριση συχνότητας σύμφωνα με το γούστο μας, να πάρουμε τον αντίστροφο μετασχηματισμό Fourier από αυτόν (είτε συνεχή είτε διακριτό) και να λάβουμε την απόκριση παλμού του συστήματος που τον υλοποιεί. Αυτό είναι απλά καταπληκτικό!
Αυτό, ωστόσο, δεν θα είναι χωρίς προβλήματα. Πρώτον, η παρορμητική απάντηση που θα λάβουμε πιθανότατα θα είναι άπειρη (δεν θα μπω σε εξηγήσεις για το γιατί, έτσι λειτουργεί ο κόσμος), οπότε θα πρέπει να πάρουμε μια ηθελημένη απόφαση να το κόψουμε κάποια στιγμή (ρύθμιση ισούται με μηδέν πέρα από αυτό το σημείο). Αλλά αυτό δεν θα συμβεί ακριβώς έτσι - η συνέπεια αυτού, όπως θα περίμενε κανείς, θα είναι η παραμόρφωση της απόκρισης συχνότητας του υπολογιζόμενου φίλτρου - θα γίνει κυματιστή και η αποκοπή συχνότητας θα είναι θολή.
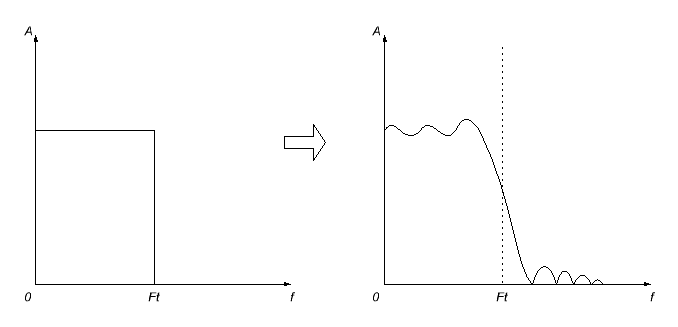
Για να ελαχιστοποιηθούν αυτά τα αποτελέσματα, διάφορες λειτουργίες παραθύρου εξομάλυνσης εφαρμόζονται στη συντομευμένη απόκριση παλμών. Ως αποτέλεσμα, η απόκριση συχνότητας συνήθως θολώνει ακόμη περισσότερο, αλλά οι δυσάρεστες (ειδικά στη ζώνη διέλευσης) ταλαντώσεις εξαφανίζονται. 
Στην πραγματικότητα, μετά από μια τέτοια επεξεργασία λαμβάνουμε μια λειτουργική παλμική απόκριση και μπορούμε να δημιουργήσουμε ένα ψηφιακό φίλτρο.
Η δεύτερη μέθοδος υπολογισμού είναι ακόμη πιο απλή - οι κρουστικές αποκρίσεις των πιο δημοφιλών φίλτρων έχουν εκφραστεί εδώ και πολύ καιρό σε αναλυτική μορφή για εμάς. Το μόνο που μένει είναι να αντικαταστήσετε τις τιμές σας και να εφαρμόσετε τη συνάρτηση παραθύρου στο αποτέλεσμα της αρεσκείας σας. Επομένως, δεν χρειάζεται καν να εξετάσετε τυχόν μετασχηματισμούς.
Και, φυσικά, εάν ο στόχος είναι να μιμηθεί τη συμπεριφορά ενός συγκεκριμένου κυκλώματος, μπορείτε να λάβετε την παλμική του απόκριση στον προσομοιωτή:
Εδώ εφάρμοσα έναν παλμό 100500 βολτ (ναι, 100,5 kV) με διάρκεια 1 μs στην είσοδο του κυκλώματος RC και απέκτησα την παλμική του απόκριση. Είναι σαφές ότι αυτό δεν μπορεί να γίνει στην πραγματικότητα, αλλά στον προσομοιωτή αυτή η μέθοδος, όπως μπορείτε να δείτε, λειτουργεί εξαιρετικά.
5. Σημειώσεις.
Αυτό που ειπώθηκε παραπάνω για τη συντόμευση της παρορμητικής απόκρισης ίσχυε, φυσικά, για το λεγόμενο. φίλτρα πεπερασμένης παλμικής απόκρισης (φίλτρα FIR/FIR). Έχουν ένα σωρό πολύτιμες ιδιότητες, συμπεριλαμβανομένης της γραμμικής φάσης (υπό ορισμένες συνθήκες για την κατασκευή της παλμικής απόκρισης), η οποία εξασφαλίζει την απουσία παραμόρφωσης του σήματος κατά το φιλτράρισμα, καθώς και την απόλυτη σταθερότητα. Υπάρχουν επίσης άπειρα φίλτρα απόκρισης παλμών (φίλτρα IIR/IIR). Είναι λιγότερο εντάσεως πόρων όσον αφορά τους υπολογισμούς, αλλά δεν έχουν πλέον τα αναφερόμενα πλεονεκτήματα.
Στο επόμενο άρθρο ελπίζω να δούμε ένα απλό παράδειγμα πρακτικής εφαρμογής ενός ψηφιακού φίλτρου.
ΚΡΑΤΙΚΟ ΠΟΛΥΤΕΧΝΕΙΟ NOVOSIBIRSK
ΣΧΟΛΗ ΑΥΤΟΜΑΤΙΣΜΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ
Τμήμα Συστημάτων Συλλογής και Επεξεργασίας Δεδομένων
Τομέας «Θεωρία και επεξεργασία σήματος»
ΕΡΓΑΣΤΗΡΙΑΚΗ ΕΡΓΑΣΙΑ ΑΡΙΘΜ.10
ΨΗΦΙΑΚΑ ΦΙΛΤΡΑ
ΜΕ ΠΕΡΙΣΜΕΝΟ ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΟΡΜΗΣ
Ομάδα:ΑΤ-33
Επιλογή: 1 Δάσκαλος:
Μαθητης σχολειου: Shadrina A.V. Αναπλ. Shchetinin Yu.I.
Στόχος της εργασίας: μελέτη μεθόδων ανάλυσης και σύνθεσης φίλτρων πεπερασμένης παλμικής απόκρισης με χρήση συναρτήσεων παραθύρου εξομάλυνσης.
Ολοκλήρωση της εργασίας:
1. Σχεδιαγράμματα παλμικής απόκρισης ενός φίλτρου FIR χαμηλής διέλευσης με συχνότητα αποκοπής ορθογώνιου παραθύρου για τιμές μήκους φίλτρου και .
Η κρουστική απόκριση ενός ιδανικού διακριτού φίλτρου FIR έχει άπειρο μήκος και είναι μη μηδενική για αρνητικές τιμές:
.
Για να αποκτήσετε ένα φυσικώς εφικτό φίλτρο, θα πρέπει να περιορίσετε την απόκριση παλμού σε έναν πεπερασμένο αριθμό και στη συνέχεια να μετατοπίσετε την περικομμένη απόκριση προς τα δεξιά κατά ένα ποσό.
Η τιμή είναι το μήκος (μέγεθος) του φίλτρου, 
– σειρά φίλτρου.
Matlab Script (labrab101.m)
N = input("Εισαγωγή μήκους φίλτρου N = ");
h = sin(wc.*(n-(N-1)/2))./(pi.*(n-(N-1)/2));
xlabel("Αριθμός αναφοράς, n")
>> υποπλοκή(2,1,1)
>> labrab101
Εισαγάγετε μήκος φίλτρου N = 15
>> title("Παρουσιακή απόκριση φίλτρου FIR για N=15")
>> υποπλοκή(2,1,2)
>> labrab101
Εισαγάγετε μήκος φίλτρου N = 50
>> title("Παρουσιακή απόκριση φίλτρου FIR για N=50")
Εικ.1. Διαγράμματα παλμικής απόκρισης ενός φίλτρου FIR χαμηλής διέλευσης με συχνότητα αποκοπής ορθογώνιου παραθύρου για τιμές μήκους φίλτρου και
Ενα σχόλιο:Αν θεωρήσουμε την απόκριση συχνότητας ενός ψηφιακού φίλτρου ως σειρά Fourier: 
, τότε οι συντελεστές αυτής της σειράς θα αντιπροσωπεύουν τις τιμές της κρουστικής απόκρισης του φίλτρου. Σε αυτήν την περίπτωση, η σειρά Fourier περικόπηκε στην πρώτη περίπτωση σε , και στη δεύτερη - σε , και στη συνέχεια τα περικομμένα χαρακτηριστικά μετατοπίστηκαν κατά μήκος του άξονα του δείγματος προς τα δεξιά για να ληφθεί ένα αιτιώδες φίλτρο. Όταν το πλάτος του κύριου λοβού είναι 2, και πότε - 1, δηλ. Καθώς το μήκος του φίλτρου αυξάνεται, ο κύριος λοβός της παλμικής απόκρισης στενεύει. Αν λάβουμε υπόψη το επίπεδο των πλευρικών λοβών (χρησιμοποιώντας ), τότε με την αύξηση αυξάνεται σε απόλυτη τιμή από σε . Έτσι, μπορούμε να συμπεράνουμε ότι όταν χρησιμοποιείται μια προσέγγιση της ιδανικής απόκρισης συχνότητας ενός φίλτρου με ορθογώνιο παράθυρο, είναι αδύνατο να περιορίσετε ταυτόχρονα τον κύριο λοβό (και επομένως να μειώσετε την περιοχή μετάβασης) και να μειώσετε τα επίπεδα των πλευρικών λοβών (μείωση κυματισμός στη ζώνη διέλευσης και στη ζώνη διακοπής του φίλτρου). Η μόνη ελεγχόμενη παράμετρος ενός ορθογώνιου παραθύρου είναι το μέγεθός του, με το οποίο μπορείτε να επηρεάσετε το πλάτος του κύριου λοβού· ωστόσο, δεν έχει μεγάλη επίδραση στους πλευρικούς λοβούς.
2. Υπολογισμός του DVFT των χαρακτηριστικών παλμών από το βήμα 1 χρησιμοποιώντας τη συνάρτηση. Γραφήματα της απόκρισης συχνότητάς τους σε γραμμική κλίμακα και σε ντεσιμπέλ για 512 δείγματα συχνότητας. Ζώνη διέλευσης, ζώνη μετάβασης και ζώνη διακοπής του φίλτρου. Η επίδραση της σειράς φίλτρου στο πλάτος της ζώνης μετάβασης και το επίπεδο απόκρισης συχνότητας κυματίζει στις ζώνες διέλευσης και διακοπής.
Λειτουργία Matlab (DTFT.m)
συνάρτηση = DTFT(x,M)
N = max(M, μήκος(x));
% Μείωση FFT σε μέγεθος 2^m
Ν = 2^(οροφή(log(N)/log(2)));
% Υπολογίστε fft
% διάνυσμα συχνότητας
w = 2*pi*((0:(N-1))/N);
w = w - 2*pi*(w>=pi);
% Μετατόπιση FFT σε εύρος από -pi έως +pi
X = fftshift(X);
w = fftshift(w);
Matlab Script (labrab102.m)
h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));
h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));
DTFT (h1,512);
DTFT (h2,512);
plot(w./(2*pi),abs(H1)./max(abs(H1)),"r")
xlabel("f, Hz"), ylabel("|H1|/max(|H1|)"), πλέγμα
plot(w./(2*pi),abs(H2)./max(abs(H2)),"b")
xlabel("f, Hz"), ylabel("|H2|/max(|H2|)"), πλέγμα
plot(w./(2*pi),20*log10(abs(H1)),"r")
title("Απόκριση συχνότητας ενός φίλτρου FIR χαμηλής διέλευσης με ορθογώνιο παράθυρο για N = 15")
xlabel("f, Hz"), ylabel("20lg(|H1|), dB"), πλέγμα
plot(w./(2*pi),20*log10(abs(H2)),"b")
title("Απόκριση συχνότητας ενός φίλτρου FIR χαμηλής διέλευσης με ορθογώνιο παράθυρο για N = 50")
xlabel("f, Hz"), ylabel("20lg(|H2|), dB"), πλέγμα
Εικ.2. Διαγράμματα απόκρισης συχνότητας ενός φίλτρου FIR χαμηλής διέλευσης με συχνότητα αποκοπής ορθογώνιου παραθύρου για τιμές μήκους φίλτρου και σε γραμμική κλίμακα
Εικ.3. Διαγράμματα απόκρισης συχνότητας ενός φίλτρου FIR χαμηλής διέλευσης με συχνότητα αποκοπής ορθογώνιου παραθύρου για τιμές μήκους φίλτρου και σε λογαριθμική κλίμακα
Ενα σχόλιο:
Τραπέζι 1. Εύρος ζώνης διέλευσης, περιοχή μετάβασης και ζώνη διακοπής για μήκος φίλτρου και
|
Μήκος φίλτρου |
Εύρος ζώνης, Hz |
Περιοχή μετάβασης, Hz |
Ζώνη διακοπής, Hz |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Διάλεξη Νο 10 "Ψηφιακά φίλτρα με πεπερασμένη απόκριση παλμών" Η συνάρτηση μεταφοράς ενός φυσικώς πραγματοποιήσιμου ψηφιακού φίλτρου πεπερασμένης απόκρισης παλμών (φίλτρο FIR) μπορεί να αναπαρασταθεί ως (10.1). Κατά την αντικατάσταση στην έκφραση (10.1), λαμβάνουμε την απόκριση συχνότητας του φίλτρου FIR στη μορφή Οπου Καθυστέρηση φάσηςτο φίλτρο ορίζεται ως Καθυστέρηση ομάδαςτο φίλτρο ορίζεται ως Ένα χαρακτηριστικό γνώρισμα των φίλτρων FIR είναι η δυνατότητα υλοποίησης σταθερών καθυστερήσεων φάσης και ομάδας, π.χ. γραμμική απόκριση φάσης (10.5), όπου ένας - σταθερό. Εάν πληρούται αυτή η προϋπόθεση, το σήμα που διέρχεται από το φίλτρο δεν παραμορφώνει το σχήμα του. Για να εξαχθούν οι συνθήκες που διασφαλίζουν μια γραμμική απόκριση φάσης, γράφουμε την απόκριση συχνότητας του φίλτρου FIR λαμβάνοντας υπόψη το (10.5) Εξισώνοντας το πραγματικό και το φανταστικό μέρος αυτής της ισότητας, παίρνουμε Διαιρώντας τη δεύτερη εξίσωση με την πρώτη, παίρνουμε Επιτέλους μπορούμε να γράψουμε Αυτή η εξίσωση έχει δύο λύσεις. Πρώτα ότανένα Το =0 αντιστοιχεί στην εξίσωση Αυτή η εξίσωση έχει μια μοναδική λύση που αντιστοιχεί σε μια αυθαίρετη h (0) (sin (0)=0) και h (n)=0 για n >0. Αυτή η λύση αντιστοιχεί σε ένα φίλτρο του οποίου η παλμική απόκριση έχει ένα μόνο μη μηδενικό δείγμα στον αρχικό χρόνο. Ένα τέτοιο φίλτρο δεν έχει πρακτικό ενδιαφέρον. Θα βρούμε άλλη λύση για . Σε αυτήν την περίπτωση, πολλαπλασιάζοντας τους αριθμητές και τους παρονομαστές στο (10.8) παίρνουμε (10.11). Από εδώ έχουμε Εφόσον αυτή η εξίσωση έχει τη μορφή σειράς Fourier, η λύση της, αν υπάρχει, είναι μοναδική. Είναι εύκολο να δούμε ότι η λύση αυτής της εξίσωσης πρέπει να ικανοποιεί τις συνθήκες (10.13), (10.14). Από την συνθήκη (10.13) προκύπτει ότι για κάθε σειρά φίλτρουΝ υπάρχει μόνο μία καθυστέρηση φάσηςένα , όπου μπορεί να επιτευχθεί αυστηρή γραμμικότητα της απόκρισης φάσης. Από την συνθήκη (10.14) προκύπτει ότι η κρουστική απόκριση του φίλτρου πρέπει να είναι συμμετρική ως προς το σημείο της περιττήςΝ , και σε σχέση με το μέσο του διαστήματος (Εικ. 10.1).
Η απόκριση συχνότητας ενός τέτοιου φίλτρου (για περιττΝ ) μπορεί να γραφτεί στη φόρμα (10.15). Πραγματοποίηση αντικατάστασης στο δεύτερο ποσό m = N -1- n , παίρνουμε (10.16). Αφού h (n)= h (N -1- n ), τότε τα δύο αθροίσματα μπορούν να συνδυαστούν Αντικαθιστώντας, παίρνουμε (10.18). Αν ορίσουμε τότε μπορούμε επιτέλους να γράψουμε Έτσι, για ένα φίλτρο με γραμμική απόκριση φάσης έχουμε Για την περίπτωση ακόμηΝ ομοίως θα έχουμε Κάνοντας αντικατάσταση στο δεύτερο άθροισμα, παίρνουμε Κάνοντας την αντικατάσταση, παίρνουμε (10.24). Έχοντας ορίσει θα έχουμε επιτέλους Έτσι, για ένα φίλτρο FIR με γραμμική απόκριση φάσης και ομοιόμορφη τάξηΤο Ν μπορεί να γραφτεί Στη συνέχεια, για λόγους απλότητας, θα εξετάσουμε μόνο φίλτρα με περιττή σειρά. Κατά τη σύνθεση της συνάρτησης μεταφοράς φίλτρου, οι αρχικές παράμετροι, κατά κανόνα, είναι οι απαιτήσεις για την απόκριση συχνότητας. Υπάρχουν πολλές τεχνικές για τη σύνθεση φίλτρων FIR. Ας δούμε μερικά από αυτά. Δεδομένου ότι η απόκριση συχνότητας οποιουδήποτε ψηφιακού φίλτρου είναι μια περιοδική συνάρτηση της συχνότητας, μπορεί να αναπαρασταθεί ως σειρά Fourier όπου οι συντελεστές της σειράς Fourier είναι ίσοι Μπορεί να φανεί ότι οι συντελεστές της σειράς Fourier h(n ) συμπίπτουν με τους συντελεστές παλμικής απόκρισης του φίλτρου. Επομένως, εάν είναι γνωστή η αναλυτική περιγραφή της απαιτούμενης απόκρισης συχνότητας του φίλτρου, τότε είναι δυνατόν να προσδιοριστούν εύκολα οι συντελεστές της παλμικής απόκρισης και από αυτούς η συνάρτηση μεταφοράς του φίλτρου. Ωστόσο, στην πράξη αυτό δεν είναι εφικτό, αφού η κρουστική απόκριση ενός τέτοιου φίλτρου έχει άπειρο μήκος. Επιπλέον, ένα τέτοιο φίλτρο δεν είναι φυσικά υλοποιήσιμο αφού η απόκριση ώθησης ξεκινά από -¥ , και καμία πεπερασμένη καθυστέρηση δεν θα καταστήσει αυτό το φίλτρο υλοποιήσιμο. Μια πιθανή μέθοδος για τη λήψη ενός φίλτρου FIR που προσεγγίζει μια δεδομένη απόκριση συχνότητας είναι η περικοπή της άπειρης σειράς Fourier και η απόκριση παλμού του φίλτρου, υποθέτοντας ότι h (n)=0 σε . Επειτα Φυσική πραγματοποίηση της συνάρτησης μεταφοράς H(z ) μπορεί να επιτευχθεί με πολλαπλασιασμό H(z) στις . Οπου (10.32). Με μια τέτοια τροποποίηση της συνάρτησης μεταφοράς, το χαρακτηριστικό πλάτους του φίλτρου δεν αλλάζει και η καθυστέρηση της ομάδας αυξάνεται κατά σταθερό ποσό. Για παράδειγμα, ας υπολογίσουμε ένα φίλτρο χαμηλής διέλευσης FIR με μια απόκριση συχνότητας της φόρμας Σύμφωνα με το (10.29), οι συντελεστές απόκρισης παλμών φίλτρου περιγράφονται με την έκφραση Τώρα από το (10.31) μπορούμε να λάβουμε μια έκφραση για τη συνάρτηση μεταφοράς Οπου (10.36). Χαρακτηριστικά πλάτους του υπολογιζόμενου φίλτρου για διάφοραΝ παρουσιάζονται στο Σχ. 10.2.
Εικ.10.2 Ο κυματισμός στη ζώνη διέλευσης και στη ζώνη διακοπής εμφανίζεται λόγω της αργής σύγκλισης της σειράς Fourier, η οποία, με τη σειρά της, προκαλείται από την παρουσία μιας ασυνέχειας στη συνάρτηση στη συχνότητα αποκοπής της ζώνης διέλευσης. Αυτοί οι παλμοί είναι γνωστοί ως Κυματισμός Gibbs. Από το Σχ. 10.2 είναι σαφές ότι με την αύξησηΝ η συχνότητα παλμών αυξάνεται και το πλάτος μειώνεται τόσο σε χαμηλότερες όσο και σε υψηλότερες συχνότητες. Ωστόσο, το πλάτος του τελευταίου κυματισμού στη ζώνη διέλευσης και του πρώτου κυματισμού στη ζώνη διακοπής παραμένουν πρακτικά αμετάβλητα. Στην πράξη, τέτοιες επιδράσεις είναι συχνά ανεπιθύμητες, κάτι που απαιτεί την εξεύρεση τρόπων μείωσης των παλμών Gibbs. Περικομμένη παλμική απόκριση h(n ) μπορεί να αναπαρασταθεί ως το γινόμενο της απαιτούμενης άπειρης παλμικής απόκρισης και μερικά λειτουργίες παραθύρου w (n) μήκους n (Εικ. 10.3).
Στην εξεταζόμενη περίπτωση απλής περικοπής της σειράς Fourier, χρησιμοποιούμε ορθογώνιο παράθυρο Σε αυτή την περίπτωση, η απόκριση συχνότητας του φίλτρου μπορεί να αναπαρασταθεί ως σύνθετη συνέλιξη Αυτό σημαίνει ότι θα είναι μια «θολή» έκδοση του απαιτούμενου χαρακτηριστικού. Το πρόβλημα έγκειται στην εύρεση συναρτήσεων παραθύρου που καθιστούν δυνατή τη μείωση του κυματισμού Gibbs με την ίδια επιλεκτικότητα φίλτρου. Για να γίνει αυτό, πρέπει πρώτα να μελετήσετε τις ιδιότητες της συνάρτησης παραθύρου χρησιμοποιώντας το παράδειγμα ενός ορθογώνιου παραθύρου. Το φάσμα της συνάρτησης ορθογώνιου παραθύρου μπορεί να γραφτεί ως Το φάσμα της συνάρτησης ορθογώνιου παραθύρου παρουσιάζεται στο Σχ. 10.4.
Εικ.10.4 Δεδομένου ότι στο , το πλάτος του κύριου λοβού του φάσματος αποδεικνύεται ίσο με . Η παρουσία πλευρικών λοβών στο φάσμα της συνάρτησης παραθύρου οδηγεί σε αύξηση του κυματισμού Gibbs στην απόκριση συχνότητας του φίλτρου. Για να επιτευχθεί χαμηλός κυματισμός στη ζώνη διέλευσης και υψηλή εξασθένηση στη ζώνη αναστολής, είναι απαραίτητο η περιοχή που περιορίζεται από τους πλευρικούς λοβούς να είναι ένα μικρό κλάσμα της περιοχής που περιορίζεται από τον κύριο λοβό. Με τη σειρά του, το πλάτος του κύριου λοβού καθορίζει το πλάτος της ζώνης μετάβασης του φίλτρου που προκύπτει. Για υψηλή επιλεκτικότητα φίλτρου, το πλάτος του κύριου λοβού πρέπει να είναι όσο το δυνατόν μικρότερο. Όπως φαίνεται από τα παραπάνω, το πλάτος του κύριου λοβού μειώνεται με την αύξηση της σειράς φίλτρου. Έτσι, οι ιδιότητες των κατάλληλων συναρτήσεων παραθύρου μπορούν να διατυπωθούν ως εξής: - η λειτουργία παραθύρου πρέπει να είναι χρονικά περιορισμένη. - το φάσμα της συνάρτησης παραθύρου θα πρέπει να προσεγγίζει καλύτερα τη συνάρτηση περιορισμένης συχνότητας, δηλ. έχουν ελάχιστη ενέργεια έξω από τον κύριο λοβό. - Το πλάτος του κύριου λοβού του φάσματος συναρτήσεων παραθύρου πρέπει να είναι όσο το δυνατόν μικρότερο. Οι πιο συχνά χρησιμοποιούμενες λειτουργίες παραθύρου είναι: 1. Ορθογώνιο παράθυρο. Συζητήθηκε παραπάνω. 2. Παράθυρο κρότου. Οπου . Αυτό το παράθυρο ονομάζεται παράθυρο Hann ( hanning). 3. Παράθυρο Blackman. 4. Το παράθυρο του Μπάρτλετ. Οι δείκτες των φίλτρων που κατασκευάστηκαν χρησιμοποιώντας τις καθορισμένες λειτουργίες παραθύρου συνοψίζονται στον Πίνακα 10.1.
Ο παράγοντας κυματισμού ορίζεται ως ο λόγος του μέγιστου πλάτους του πλευρικού λοβού προς το πλάτος του κύριου λοβού στο φάσμα της συνάρτησης παραθύρου. Για να επιλέξετε την απαιτούμενη σειρά φίλτρων και την καταλληλότερη λειτουργία παραθύρου κατά τον υπολογισμό των πραγματικών φίλτρων, μπορείτε να χρησιμοποιήσετε τα δεδομένα στον Πίνακα 10.2.
Όπως φαίνεται από τον Πίνακα 10.1, υπάρχει μια ορισμένη σχέση μεταξύ του συντελεστή κυματισμού και του πλάτους του κύριου λοβού στο φάσμα της συνάρτησης παραθύρου. Όσο μικρότερος είναι ο συντελεστής παλμών, τόσο μεγαλύτερο είναι το πλάτος του κύριου λοβού και επομένως η ζώνη μετάβασης στην απόκριση συχνότητας του φίλτρου. Για να εξασφαλιστεί χαμηλός κυματισμός στη ζώνη διέλευσης, είναι απαραίτητο να επιλέξετε ένα παράθυρο με κατάλληλο συντελεστή κυματισμού και να παρέχετε το απαιτούμενο πλάτος της ζώνης μετάβασης με αυξημένη σειρά φίλτρου N. Αυτό το πρόβλημα μπορεί να λυθεί χρησιμοποιώντας το παράθυρο που προτείνει ο Kaiser. Η συνάρτηση παραθύρου Kaiser έχει τη μορφή
όπου a είναι μια ανεξάρτητη παράμετρος,
Μια ελκυστική ιδιότητα του παραθύρου Kaiser είναι η δυνατότητα ομαλή αλλαγή του συντελεστή παλμών από μικρές σε μεγάλες τιμές, ενώ αλλάζει μόνο μία παράμετρος α. Σε αυτήν την περίπτωση, όπως και για άλλες λειτουργίες παραθύρου, το πλάτος του κύριου λοβού μπορεί να ρυθμιστεί με τη σειρά φίλτρου N. Οι κύριες παράμετροι που ορίζονται κατά την ανάπτυξη ενός πραγματικού φίλτρου είναι: Εύρος ζώνης - w p ; Λωρίδα εμποδίων - w a ; Ο μέγιστος επιτρεπόμενος κυματισμός στη ζώνη διέλευσης είναι A p ; Ελάχιστη εξασθένηση ζώνης διακοπής – A a ; -συχνότητα δειγματοληψίας - ws. Αυτές οι παράμετροι απεικονίζονται στο Σχ. 10.5. Σε αυτήν την περίπτωση, ο μέγιστος κυματισμός στη ζώνη διέλευσης καθορίζεται ως
και η ελάχιστη εξασθένηση στη ζώνη διακοπής είναι όσο Η σχετικά απλή διαδικασία για τον υπολογισμό ενός φίλτρου με ένα παράθυρο Kaiser περιλαμβάνει τα ακόλουθα βήματα: 1. Προσδιορίζεται η κρουστική απόκριση του φίλτρου h (n), με την προϋπόθεση ότι η απόκριση συχνότητας είναι ιδανική
όπου (10.49). 2. Η παράμετρος d επιλέγεται ως
Οπου 3. Η πραγματική τιμή των A a και A p υπολογίζεται χρησιμοποιώντας τους τύπους (10.46), (10.47). 4.Η παράμετρος a επιλέγεται ως
5.Η παράμετρος D επιλέγεται ως
6. Επιλέξτε τη μικρότερη περιττή τιμή της σειράς φίλτρου από τη συνθήκη
ακολουθεί ότι Δεδομένου ότι τα δείγματα της κρουστικής απόκρισης του φίλτρου είναι οι συντελεστές της συνάρτησης μεταφοράς του, η συνθήκη (10.59) σημαίνει ότι οι κωδικοί όλων των συντελεστών φίλτρου περιέχουν μόνο το κλασματικό μέρος και το bit πρόσημου και δεν περιέχουν το ακέραιο μέρος. Ο αριθμός των ψηφίων του κλασματικού τμήματος των συντελεστών φίλτρου καθορίζεται από την προϋπόθεση της ικανοποίησης της συνάρτησης μεταφοράς φίλτρου με κβαντισμένους συντελεστές, τις καθορισμένες απαιτήσεις για την προσέγγιση της συνάρτησης μεταφοράς αναφοράς με ακριβείς τιμές των συντελεστών. Οι απόλυτες τιμές των δειγμάτων σήματος εισόδου φίλτρου συνήθως κανονικοποιούνται έτσι ώστε Εάν η ανάλυση πραγματοποιείται για ένα φίλτρο FIR με γραμμική απόκριση φάσης, τότε ο αλγόριθμος για τον υπολογισμό του σήματος εξόδου του μπορεί να είναι ο ακόλουθος όπου οι συντελεστές φίλτρου στρογγυλοποιούνται σε s k. Αυτός ο αλγόριθμος αντιστοιχεί στο μπλοκ διάγραμμα φίλτρου που φαίνεται στην Εικ. 10.5.
Υπάρχουν δύο τρόποι υλοποίησης αυτού του αλγόριθμου. Στην πρώτη περίπτωση, όλες οι πράξεις πολλαπλασιασμού εκτελούνται ακριβώς και δεν υπάρχει στρογγυλοποίηση γινομένων. Σε αυτήν την περίπτωση, το βάθος bit των γινομένων είναι ίσο με s σε +s k, όπου s in είναι το βάθος bit του σήματος εισόδου και s k είναι το βάθος bit των συντελεστών φίλτρου. Σε αυτήν την περίπτωση, το μπλοκ διάγραμμα του φίλτρου που φαίνεται στο Σχ. 10.5 αντιστοιχεί ακριβώς στο πραγματικό φίλτρο. Στη δεύτερη μέθοδο υλοποίησης του αλγορίθμου (10.61), κάθε αποτέλεσμα της πράξης πολλαπλασιασμού στρογγυλοποιείται, δηλ. τα προϊόντα υπολογίζονται με κάποιο λάθος. Σε αυτήν την περίπτωση, είναι απαραίτητο να αλλάξει ο αλγόριθμος (10.61) ώστε να ληφθεί υπόψη το σφάλμα που εισάγεται με τη στρογγυλοποίηση των γινομένων Εάν οι τιμές δείγματος του σήματος εξόδου του φίλτρου υπολογίζονται χρησιμοποιώντας την πρώτη μέθοδο (με ακριβείς τιμές των προϊόντων), τότε η διασπορά του θορύβου εξόδου προσδιορίζεται ως
εκείνοι. εξαρτάται από τη διακύμανση του θορύβου στρογγυλοποίησης του σήματος εισόδου και τις τιμές των συντελεστών φίλτρου. Από εδώ μπορείτε να βρείτε τον απαιτούμενο αριθμό bit του σήματος εισόδου ως
Χρησιμοποιώντας τις γνωστές τιμές των s in και s k, μπορεί κανείς να προσδιορίσει τον αριθμό των bit που απαιτούνται για το κλασματικό μέρος του κωδικού σήματος εξόδου ως Εάν οι τιμές των δειγμάτων σήματος εξόδου υπολογίζονται χρησιμοποιώντας τη δεύτερη μέθοδο, όταν κάθε γινόμενο στρογγυλοποιείται σε ψηφία s d, τότε η διασπορά του θορύβου στρογγυλοποίησης που δημιουργείται από κάθε έναν από τους πολλαπλασιαστές μπορεί να εκφραστεί ως προς την χωρητικότητα των ψηφίων του προϊόν ως DR in και αναλογία σήματος προς θόρυβο στην έξοδο του φίλτρου SNR out. Το δυναμικό εύρος του σήματος εισόδου σε ντεσιμπέλ ορίζεται ως
όπου A max και A min είναι το μέγιστο και το ελάχιστο πλάτος του σήματος εισόδου του φίλτρου. Ο λόγος σήματος προς θόρυβο στην έξοδο του φίλτρου, εκφρασμένος σε ντεσιμπέλ, ορίζεται ως
καθορίζει τη μέση τετραγωνική τιμή ρίζας της ισχύος του ημιτονοειδούς σήματος εξόδου του φίλτρου με πλάτος A min, και (10.77) καθορίζει την ισχύ του θορύβου στην έξοδο του φίλτρου. Από (10.75) και (10.76) με A max =1 λαμβάνουμε μια έκφραση για τη διασπορά του θορύβου εξόδου του φίλτρου Αυτή η τιμή διασποράς θορύβου εξόδου φίλτρου μπορεί να χρησιμοποιηθεί για τον υπολογισμό του βάθους bit των σημάτων εισόδου και εξόδου του φίλτρου.  Ο κόσμος των δωρεάν προγραμμάτων και χρήσιμες συμβουλές 2024 whatsappss.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(10.2),
- Απόκριση πλάτους-συχνότητας (AFC)φίλτρο,
- απόκριση συχνότητας φάσης (PFC)φίλτρο.
(10.3).
(10.4).
(10.6).
(10.7).
(10.8).
(10.9).
(10.10).
(10.12).
(10.17).
(10.19),
(10.20).
(10.21).
(10.22).
(10.23).
(10.25),
(10.26).
(10.27).
(10.28),
(10.29).
(10.30).
(10.31),
(10.33).
(10.34).
(10.35),
(10.37).
(10.38).
(10.39).
(10.40).
(10.41),
(10.42).
(10.43).
(10.44),
, I 0 – Συνάρτηση Bessel του πρώτου είδους μηδενικής τάξης, που ορίζεται από την έκφραση
(10.45).
(10.46),
(10.50),
(10.51).
(10.52).
(10.53).
(10.54),
(10.57)
(10.66),
(10.67).
(10.74),
(10.75),
(10.78).