Filtrning impulsli javobi. Cheklangan impulsli javobli raqamli filtrlar. Ma'lumotlarni tekislash. Median filtrlash
48 Cheklangan impulsli javobli raqamli filtrlar. Kih filtrlarini hisoblash.
Cheklangan impulsli javob filtri (Rekursiv bo'lmagan filtr, FIR filtri) yoki FIR filtri (FIR chekli impuls javobidan qisqartirilgan - chekli impulsli javob) - chiziqli raqamli filtrlarning turlaridan biri, xarakterli xususiyati vaqt chegarasi. impulsli javob(bir vaqtning o'zida u nolga teng bo'ladi). Bunday filtr qayta aloqa yo'qligi sababli rekursiv bo'lmagan deb ham ataladi. Bunday filtrning uzatish funktsiyasining maxraji ma'lum bir doimiydir.
Filtrning kirish va chiqish signallari o'rtasidagi munosabatni tavsiflovchi farq tenglamasi: bu erda P- filtrlash tartibi, x(n) - kirish signali, y(n) chiqish signalidir, va b i- filtrlash koeffitsientlari. Boshqacha qilib aytganda, har qanday chiqish signali namunasining qiymati o'lchovli qiymatlar yig'indisi bilan aniqlanadi P oldingi o'qishlar. Siz buni boshqacha aytishingiz mumkin: har qanday vaqtda filtr chiqishi qiymati kirishning bir lahzali qiymatiga javob qiymati va barcha asta-sekin parchalanadigan javoblarning yig'indisidir. P chiqishga ta'sir qiladigan oldingi signal namunalari (keyin P-hisoblanadi, impuls o'tish funktsiyasi nolga teng bo'ladi, yuqorida aytib o'tilganidek, shuning uchun keyin barcha atamalar P-th ham nolga teng bo'ladi). Oldingi tenglamani yanada kengroq shaklda yozamiz:
Filtr yadrosini topish uchun biz qo'yamiz
x(n) = δ( n)
qaerda d( n) - delta funktsiyasi. Keyin FIR filtrining impuls javobini quyidagicha yozish mumkin:
Impuls javobining Z-transformatsiyasi bizga FIR filtrining uzatish funktsiyasini beradi:
]Xususiyatlar
FIR filtri bir qator foydali xususiyatlarga ega bo'lib, uni ba'zan IIR filtridan ko'ra foydalanish afzalroq qiladi. Mana ulardan ba'zilari:
FIR filtrlari mustahkam.
FIR filtrlari amalga oshirilganda fikr-mulohazalarni talab qilmaydi.
FIR filtrlarining fazasi chiziqli bo'lishi mumkin
FIR filtrining bevosita shakli
FIR filtrlari uchta element yordamida amalga oshirilishi mumkin: multiplikator, to'ldiruvchi va kechikish bloki. Rasmda ko'rsatilgan variant 1-toifa FIR filtrlarining to'g'ridan-to'g'ri amalga oshirilishidir.
FIR filtrining bevosita shaklini amalga oshirish
Misol dasturi
Quyida C tilida yozilgan FIR filtri dasturining namunasi keltirilgan:
/* 128 marta bosish uchun FIR filtri */
float fir_filtr(float kiritish)
statik float namunasi;
acc = 0,0f; /* Batareya */
/* Ko‘paytirish va to‘plash */
uchun (i = 0; i< 128; i++) {
acc += (h[i] * namuna [i]);
/* Chiqish */
/* Kechiktirilgan signalni o'zgartiring */
uchun (i = 127; i > 0; i--)
namuna [i] = namuna;
49 Ma'lumotlarni tekislash. Harakatlanuvchi o'rtacha.
50 Ma'lumotlarni tekislash. Parabolik tekislash.
51 Ma'lumotlarni tekislash. Spenser silliqlash.
52 Ma'lumotlarni tekislash. Median filtrlash.
Harakatlanuvchi o'rtacha, parabolik tekislash, Spenser tekislash, median filtrlash
Vaqt o'tishi bilan sekin o'zgarib turadigan jismoniy jarayonlarning parametrlarini aniqlash usullarini ishlab chiqishda muhim vazifa shovqin effektlari yoki birlamchi konvertorning chiqishida olingan qayta ishlangan signalga qo'shiladigan tasodifiy shovqinlarning ta'sirini bartaraf etishdir.
Ushbu ta'sirni bartaraf qilish uchun siz ma'lumotlarni tekislashni qo'llashingiz mumkin. Bunday tekislashning eng oddiy usullaridan biri arifmetik o'rtacha hisoblashdir. Undan foydalanganda diskret funktsiyaning har bir qiymati (qayta ishlangan ma'lumotlar massivi) quyidagi ifodaga muvofiq hisoblanadi:
qayerda o'rtacha arifmetik ballar soni (toq butun son);
Funktsiyaning qayta ishlashdan oldingi qiymati;
Boshqa juda samarali usullar mavjud, masalan, ikkinchi darajali parabolalar bilan besh, etti, to'qqiz va o'n bir nuqtadagi ifodalarga muvofiq:
yoki etti, to'qqiz, o'n bir va o'n uch nuqtadagi to'rtinchi darajali parabolalar:
Amaliy qo'llanmalarda boshqa samarali usullar, masalan, 15 nuqtali Spenser silliqlash yaxshi natijalar beradi:
Kompleks eksponensialni ushbu ifodalarning o'rniga qo'yish orqali biz mos transformatsiyaning uzatish funktsiyasini aniqlashimiz mumkin.
Arifmetik o'rtacha hisoblash uchun
Qavslar ichidagi ifoda maxrajli geometrik progressiyani ifodalaydi, shuning uchun bu ifoda quyidagicha ifodalanishi mumkin:
.
Ushbu formula past chastotali filtrning uzatish xarakteristikasini ifodalaydi va u ko'rsatadiki, o'rtacha hisoblashda qancha atamalar ishtirok etsa, signaldagi yuqori chastotali shovqin komponentlarini bostirish shunchalik ko'p bo'ladi (6.1-rasmga qarang).
Biroq, vaqt tendentsiyalarini qayta ishlashda chastotaning semantik tushunchasi signallarni qayta ishlashda shunga o'xshash tushunchadan farq qiladi. Bu shunisi bilan izohlanadiki, vaqt tendentsiyalarini o'rganishda ularning chastota tarkibi emas, balki o'zgarish turi (o'sish, pasayish, doimiylik, tsikliklik va boshqalar) qiziqish uyg'otadi.
Ma'lumotlarni tekislash uchun evristik algoritmlardan foydalanish ham juda samarali.
Ulardan biri median filtrlashdir. Uni amalga oshirish davomida o'lchamdagi to'g'ri keladigan vaqt oynasida, butun son toq son bo'lsa, markaziy element ketma-ketlikning o'rta elementi bilan almashtiriladi, ular qiymatlarning o'sish tartibida, silliqlangan ma'lumotlar massivining elementlari bilan tartibga solinadi. signal vaqt oynasiga tushadi. Median filtrlashning afzalligi impulsli shovqinni olib tashlash qobiliyatidir, uning davomiyligi oshmaydi, deyarli silliq o'zgaruvchan signallarni buzmasdan. Shovqinni bostirishning bu usuli qat'iy matematik asosga ega emas, ammo hisob-kitoblarning soddaligi va olingan natijalarning samaradorligi uning keng qo'llanilishiga olib keldi.
6.1-rasm - Xarakteristik grafiklarni uzatish
m=5, 7, 9, 11 uchun arifmetik o'rtacha amallar
Yana bir qiziqarli silliqlash algoritmi o'rtacha o'rtacha hisoblanadi. Uning mohiyati quyidagicha. O'lchamdagi siljish vaqti oynasida (-toq butun son) ma'lumotlar massivining elementlari o'sish tartibida tartibga solinadi, so'ngra birinchi va oxirgi elementlar tartiblangan ketma-ketlikdan chiqariladi (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
Bu usul impuls va radiochastota shovqinlarini bostirishga, shuningdek signalning yaxshi tekislanishiga erishishga imkon beradi.
| " |
Keling, raqamli filtrlarning eng oddiylarini ko'rib chiqaylik - doimiy parametrlarga ega filtrlar.
Raqamli filtrning kirish signali raqamli qiymatlar ketma-ketligi ko'rinishida, oraliqlar bilan ta'minlanadi (4.1-rasm, a). Raqamli filtrda har bir keyingi signal qiymati qabul qilinganda, chiqish signalining keyingi qiymati hisoblanadi Hisoblash algoritmlari juda xilma-xil bo'lishi mumkin; hisoblash jarayonida, kirish signalining oxirgi qiymatidan tashqari, foydalanish mumkin
Kirish va chiqish signallarining oldingi qiymatlari: Raqamli filtrning chiqish signali ham oraliqdan keyingi raqamli qiymatlar ketma-ketligidir. Bu interval butun raqamli signalni qayta ishlash qurilmasi uchun bir xil.
Guruch. 4.1. Raqamli filtrning kirish va chiqishidagi signal
Shuning uchun, agar siz raqamli filtrning kirishiga bitta impuls ko'rinishidagi eng oddiy signalni qo'llasangiz (4.2-rasm, a)
keyin chiqishda biz raqamli qiymatlarning diskret ketma-ketligi ko'rinishidagi signalni olamiz
An'anaviy analog sxemalarga o'xshab, biz bu javob signalini filtrning impulsli javobi deb ataymiz (4.2-rasm, b). Analog zanjirning impuls javobidan farqli o'laroq, funksiya o'lchovsizdir.
Guruch. 4.2. Raqamli filtrning birlik impulsi va impuls javobi
Filtrni kiritishga ixtiyoriy diskret signalni qo'llaymiz (1-rasm). 4.1, a), bu diskret qiymatlar to'plamidir
Birinchi elementning ta'sirida filtrning chiqishida ga ko'paytiriladigan ketma-ketlik hosil bo'ladi, harakat ostida ketma-ketlik miqdorga ko'paytiriladi va o'ngga siljiydi va hokazo. Natijada, chiqish hosil bo'ladi. ketma-ketlik qaerda
Shunday qilib, chiqish signali kirish signalining diskret konvolyutsiyasi va impuls javobi sifatida aniqlanadi. Shu nuqtai nazardan, raqamli filtrlar an'anaviy sxemalarga o'xshaydi, bu erda chiqish signali kirish signalining konvolyutsiyasi va impuls javobiga teng.
Formula (4.1) raqamli filtrlash algoritmidir. Agar filtrning impulsli javobi chekli sonli atamalar bilan ketma-ketlik bilan tavsiflangan bo'lsa, u holda filtr shaklda ko'rsatilgan sxema ko'rinishida amalga oshirilishi mumkin. 4.3. Bu erda harf vaqt uchun signalni kechiktirish elementlarini ko'rsatadi (har bir hujayra uchun); -signalni mos keladigan koeffitsientga ko'paytiruvchi elementlar.
Shaklda ko'rsatilgan diagramma. 4.3 raqamli filtrning elektr davri emas; Ushbu diagramma raqamli filtrlash algoritmining grafik tasviri bo'lib, signalni qayta ishlash jarayonida bajariladigan arifmetik amallar ketma-ketligini ko'rsatadi.
Guruch. 4.3. Rekursiv bo'lmagan raqamli filtr sxemasi
Signallarni mavhum raqamli ketma-ketliklar shaklida qayta ishlovchi raqamli filtrlar uchun "vaqtni kechiktirish" tushunchasi butunlay to'g'ri emas. Shuning uchun signalni bitta katakchaga kechiktiradigan elementlar odatda raqamli filtr sxemalarida -transformatsiyalar tilida signal kechikishini ko'rsatadigan belgi bilan belgilanadi. Keyinchalik biz ushbu belgiga amal qilamiz.
Keling, rasmda ko'rsatilgan raqamli filtr sxemasiga qaytaylik. 4.3, Hisoblash uchun faqat kirish signalining qiymatlari qo'llaniladigan bunday filtrlar oddiy yoki rekursiv bo'lmagan deb ataladi.
Filtrning impulsli javobi ma'lum bo'lsa, rekursiv bo'lmagan filtr algoritmini yozish oson. Algoritmni amaliy amalga oshirish uchun impuls javobi cheklangan miqdordagi atamalarni o'z ichiga olishi kerak. Agar impulsli javob cheksiz sonli atamalarni o'z ichiga olsa-da, lekin ular tezda qiymatini kamaytirsa, unda siz o'zingizni cheklangan miqdordagi atamalar bilan cheklab, qiymatlari kichik bo'lganlardan voz kechishingiz mumkin. Agar impuls javobining elementlari qiymati kamaymasa, rekursiv bo'lmagan filtr algoritmi amalga oshirib bo'lmaydigan bo'lib chiqadi.
Guruch. 4.4. -zanjir
Misol tariqasida -sxemaga o'xshash eng oddiy raqamli filtrni ko'rib chiqing (4.4-rasm). Devrenning impulsli javobi shaklga ega
Tegishli raqamli filtrning impuls javobini yozish uchun ifoda bilan almashtirilishi kerak Biroq, kontaktlarning zanglashiga olib keladigan impuls javobi o'lchovga ega va raqamli filtrning impulsli javobi o'lchovsiz bo'lishi kerak. Shuning uchun (4.2) ifodada ko'paytuvchini o'tkazib yuboramiz va raqamli filtrning impuls javobini shaklda yozamiz.
Bunday impuls javobi cheksiz ko'p atamalarni o'z ichiga oladi, lekin ularning kattaligi eksponensial qonunga ko'ra kamayadi va biz o'zimizni atamalar bilan cheklab, shunday tanlashimiz mumkin.
Endi biz signalning ifodasini filtr chiqishida yozishimiz mumkin
Bu ifoda ham raqamli filtr algoritmidir. Ushbu filtrning diagrammasi rasmda ko'rsatilgan. 4.5.
Raqamli filtrlarda jarayonlarni tahlil qilishning ikkinchi usuli an'anaviy analog sxemalarni tahlil qilishning operator usuliga o'xshaydi, faqat Laplas konvertatsiyasi o'rniga -transformatsiyasi qo'llaniladi.
Guruch. 4.5. -sxemaga o'xshash rekursiv bo'lmagan raqamli filtrning sxemasi
Elektr zanjirining uzatish funktsiyasiga o'xshash raqamli filtr parametrini aniqlaymiz. Buning uchun raqamli filtrning impuls javobiga o'zgartirish kiriting:
Funktsiya tizim filtri funktsiyasi deb ataladi.
(4.1) ifodaga muvofiq, raqamli filtrning chiqishidagi signal kirish signalining diskret konvolyutsiyasiga va filtrning impulsli javobiga teng. Ushbu ifodaga konvolyutsiya teoremasini qo'llagan holda, chiqish signalining o'zgarishi tizim filtri funktsiyasi bilan ko'paytirilgan kirish signalining o'zgarishiga teng ekanligini bilib olamiz:
Shunday qilib, tizim funktsiyasi raqamli filtrning uzatish funktsiyasi rolini o'ynaydi.
Misol tariqasida, sxemaga o'xshash birinchi tartibli raqamli filtrning tizim funksiyasini topamiz:
Raqamli filtrlar orqali signallarning o'tishini tahlil qilishning uchinchi usuli differensial tenglamalarning klassik usuliga o'xshaydi. Keling, misol sifatida buyurtma zanjirlaridan foydalangan holda ushbu usulni ko'rib chiqaylik.
1-tartibning eng oddiy analog sxemasi -sxema (4.4-rasmga qarang), signallarning o'tishi differentsial tenglama bilan tavsiflanadi.
Diskret sxema uchun differentsial tenglama (4.8) o'rniga farq tenglamasi yozilishi kerak, bu erda kirish va chiqish signallari vaqtning diskret momentlari uchun ko'rsatilgan va hosila o'rniga qo'shni signal qiymatlari farqi bo'lishi kerak. paydo bo'ladi. Diskret 1-tartibli sxema uchun ayirma tenglamasi ancha umumiy shaklda yozilishi mumkin
O'zgartirishni tenglamaga qo'llaymiz
bu erda biz tizim filtri funksiyasini topamiz
Formula (4.10) 1-tartibli raqamli filtrning tizim funksiyasi uchun juda umumiy ifodadir. Raqamli filtrning tizim funktsiyasi uchun oldindan olingan ifoda (4.7) bilan mos kelganda - sxemaga ekvivalent.
Tizim funksiyasiga (4.10) mos keladigan raqamli filtrlash algoritmini topamiz. Buning uchun (4.9) tenglamani yechamiz
Ushbu algoritmning ekvivalent diagrammasi rasmda ko'rsatilgan. 4.6. Rekursiv bo'lmagan filtr bilan solishtirganda (4.5-rasmga qarang) bu erda "teskari aloqa davri" qo'shilgan, ya'ni chiqish signalining qiymatlari keyingi bosqichlarda qo'llaniladi.
Guruch. 4.6. -sxemaga o'xshash rekursiv raqamli filtrning sxemasi
hisob-kitoblar. Ushbu turdagi filtrlar rekursiv deb ataladi.
Algoritm (4.11) avval ko'rib chiqilgan rekursiv bo'lmagan filtrga to'liq ekvivalent bo'lgan filtrga mos keladi. Ammo rekursiv bo'lmagan filtr algoritmi (4.4) yordamida chiqish signalining bir qiymatini aniqlash uchun operatsiyalarni bajarish kerak va rekursiv filtrlash algoritmidan (4.11) foydalanganda faqat ikkita operatsiya kerak bo'ladi. Bu rekursiv filtrlarning asosiy afzalligi. Bundan tashqari, rekursiv filtrlar signalni yuqori aniqlik bilan qayta ishlashga imkon beradi, chunki ular impuls javobini uning "dumini" tashlamasdan to'g'riroq amalga oshirishga imkon beradi. Rekursiv filtrlar rekursiv bo'lmagan filtrlar yordamida umuman amalga oshirib bo'lmaydigan algoritmlarni amalga oshirish imkonini beradi. Masalan, shakldagi sxema bo'yicha ishlaydigan filtr bilan. 4.6, mohiyatan ideal akkumulyator-integrator bo'lib, impulsli javobga ega bo'lib, bunday xususiyatga ega bo'lgan filtrni rekursiv bo'lmagan sxema yordamida amalga oshirish mumkin emas.
Ko'rib chiqilgan misollar uzoq impulsli javobli raqamli filtrlarni yaratish uchun rekursiv bo'lmagan algoritmlardan foydalanishning ma'nosi yo'qligini ko'rsatadi. Bunday hollarda rekursiv filtrlardan foydalanish maqsadga muvofiqdir.
Rekursiv bo'lmagan algoritmlarni qo'llash sohasi - bu kam sonli atamalarni o'z ichiga olgan impulsli javobli raqamli filtrlarni amalga oshirish. Masalan, chiqish signali kirish signalining o'sishiga teng bo'lgan eng oddiy differentsiator:
Bunday raqamli filtrning sxemasi rasmda ko'rsatilgan. 4.7.
Guruch. 4.7. Eng oddiy raqamli differentsialning sxemasi
Keling, tenglama bilan tavsiflangan umumiy raqamli filtrni ko'rib chiqaylik
Ushbu tenglamani tartibning farq tenglamasi sifatida ham, raqamli filtrlash algoritmi sifatida ham ko'rib chiqish mumkin, agar u boshqacha tarzda qayta yozilsa, ya'ni
Guruch. 4.8. Rekursiv raqamli tartibli filtr sxemasi
Algoritm (4.13) rasmda ko'rsatilgan sxemaga mos keladi. 4.8. Keling, bunday filtrning tizim funktsiyasini topamiz. Buning uchun tenglamaga o'zgartirishni qo'llang:
Ifoda (4.14) filtrlash sxemasi elementlarining tebranishlari va tizim funktsiyasi o'rtasidagi bog'liqlikni o'rnatishga imkon beradi. Tizim funksiyasining numeratoridagi koeffitsientlar uchun koeffitsientlarning qiymatlarini aniqlaydi
(filtrning rekursiv bo'lmagan qismida) va maxrajdagi koeffitsientlar filtrning rekursiv qismini aniqlaydi.
Hammasi do'st do'stining do'sti xuddi shu filtrlar bilan yordamga muhtoj bo'lganida boshlandi. Jedi yo'llari orqali bu haqda mish-mishlar menga etib keldi, men havoladagi postga sharhlarda obunani bekor qildim. Bu yordam bergandek tuyuldi. Xo'sh, umid qilaman.
Bu hikoya menda uchinchi yoki shunga o'xshash narsa haqida xotiralarni uyg'otdi, men o'zim DSP ni olganimda va meni raqamli filtrlar qanday ishlashiga qiziqqan, lekin tabiiy ravishda qo'rqqanlar uchun maqola yozishga undadi. -eng yaxshi formulalar va psixik chizmalar (men allaqachon darsliklar haqida gapirmayapman).
Umuman olganda, mening tajribamga ko'ra, darsliklar bilan bog'liq vaziyat ba'zan daraxtlar uchun o'rmonni ko'ra olmaysiz degan mashhur ibora bilan tasvirlangan. Ya'ni, ular sizni Z-transformatsiyasi va ko'pincha ikki doskadan uzunroq bo'lgan polinomlarni bo'lish formulalari bilan qo'rqitishni boshlaganlarida, mavzuga qiziqish juda tez so'nadi. Biz oddiydan boshlaymiz, xayriyatki, nima bo'layotganini tushunish uchun uzoq murakkab iboralarni tasvirlashning hojati yo'q.
Shunday qilib, birinchi navbatda, ba'zi oddiy asosiy tushunchalar.
1. Impulsli javob.
Aytaylik, bizda to'rtta pinli quti bor. Biz ichkarida nima borligini bilmaymiz, lekin ikkita chap terminal kirish va ikkita o'ng terminal chiqish ekanligini aniq bilamiz. Keling, unga juda katta amplitudali juda qisqa pulsni qo'llashga harakat qilaylik va chiqishda nima sodir bo'lishini ko'rib chiqaylik. Xo'sh, bu to'rtburchak ichida nima borligi aniq emas, chunki uni qanday tasvirlash aniq emas, lekin hech bo'lmaganda biz biror narsani ko'ramiz.
Bu erda shuni aytish kerakki, nazariy jihatdan katta (umuman aytganda, cheksiz) amplitudaning qisqa (umuman aytganda, cheksiz qisqa) zarbasi delta funktsiyasi deb ataladi. Aytgancha, kulgili narsa shundaki, buning ajralmas qismi cheksiz funksiya birga teng. Bu normalizatsiya.
Shunday qilib, biz kirishga delta funktsiyasini qo'llagan holda to'rt kutupli tarmoqning chiqishida ko'rgan narsamiz deyiladi. impulsli javob bu to'rtburchak. Biroq, hozircha, bu bizga qanday yordam berishi aniq emas, lekin faqat olingan natijani eslaylik va keyingi qiziqarli kontseptsiyaga o'tamiz.
2. Konvolyutsiya.
Muxtasar qilib aytganda, konvolyutsiya - bu funktsiyalar mahsulotini integrallashdan kelib chiqadigan matematik operatsiya:
Ko'rib turganingizdek, u yulduzcha bilan ko'rsatilgan. Bundan tashqari, konvolyutsiya paytida bitta funktsiya "oldinga" tartibda qabul qilinishini va biz ikkinchisidan "oldinga" o'tishini ko'rishingiz mumkin. Albatta, insoniyat uchun qimmatroq bo'lgan diskret holatda konvolyutsiya, har qanday integral kabi, yig'indiga kiradi:
Bu qandaydir zerikarli matematik mavhumlik kabi ko'rinadi. Biroq, aslida, o'ram bu dunyodagi eng sehrli hodisa bo'lib, u odamning tug'ilishidan keyin ikkinchi o'rinda turadi, yagona farq shundaki, ko'pchilik bolalar qayerdan kelganini kamida yoshida bilib oladi. o'n sakkizda, konvolyutsiya nima va u nima uchun foydali va hayratlanarli ekanligi haqida, Yer aholisining katta qismi butun umri davomida umuman tasavvurga ega emas.
Shunday qilib, bu operatsiyaning kuchi shundan iboratki, agar f har qanday ixtiyoriy kirish signali va g to'rt portli tarmoqning impulsli javobi bo'lsa, u holda bu ikki funktsiyaning konvolyutsiyasi natijasi biz qilgan narsaga o'xshash bo'ladi. Ushbu to'rt portli tarmoq orqali f signalini o'tkazish orqali oling.
Ya'ni, impulsli javob kirish effektiga nisbatan to'rt portli tarmoqning barcha xususiyatlarining to'liq to'plamidir va u bilan kirish signalining konvolyutsiyasi mos keladigan chiqish signalini tiklashga imkon beradi. Menimcha, bu shunchaki ajoyib!
3. Filtrlar.
Siz impulsli javob va konvolyutsiya bilan juda ko'p qiziqarli narsalarni qilishingiz mumkin. Misol uchun, agar signal audio bo'lsa, siz reverb, echo, xor, flanger va boshqa ko'p narsalarni tashkil qilishingiz mumkin; farqlash va birlashtirish mumkin ... Umuman olganda, siz har qanday narsani yaratishingiz mumkin. Biz uchun hozir eng muhimi shundaki, albatta, filtrlarni konvolyutsiya yordamida ham osongina olish mumkin.
Raqamli filtrning o'zi kerakli filtrga mos keladigan impulsli javob bilan kirish signalining konvolyutsiyasidir.
Lekin, albatta, impuls javobini qandaydir tarzda olish kerak. Albatta, biz uni qanday o'lchashni yuqorida bilib oldik, lekin bunday vazifada buning ma'nosi yo'q - agar biz filtrni yig'ib olgan bo'lsak, nima uchun boshqa narsani o'lchashimiz mumkin, biz uni avvalgidek ishlatishimiz mumkin. Bundan tashqari, raqamli filtrlarning eng muhim qiymati shundaki, ular haqiqatda erishib bo'lmaydigan (yoki erishish juda qiyin) xususiyatlarga ega bo'lishi mumkin - masalan, chiziqli faza. Shunday qilib, bu erda o'lchashning hech qanday usuli yo'q, siz faqat hisoblashingiz kerak.
4. Impulsli javobni olish.
Shu nuqtada, mavzu bo'yicha ko'pgina nashrlarda mualliflar o'quvchini butunlay chalkashtirib, Z-transformatsiyalari va ko'phadlardan kasrlarni to'plashni boshlaydilar. Men buni qilmayman, men bularning barchasi nima haqida ekanligini va nima uchun amalda ilg'or jamoatchilik uchun juda zarur emasligini qisqacha tushuntiraman.
Aytaylik, biz filtrdan nimani xohlashimizni aniqladik va uni tavsiflovchi tenglamani yaratdik. Keyinchalik, impuls javobini topish uchun siz delta funktsiyasini olingan tenglamaga almashtirib, kerakli narsani olishingiz mumkin. Bitta muammo - buni qanday qilish kerak, chunki delta funktsiyasi o'z vaqtida O th mintaqasi ayyor tizim tomonidan berilgan va umuman olganda, har xil cheksizliklar mavjud. Shunday qilib, bu bosqichda hamma narsa juda qiyin bo'lib chiqadi.
Bu erda ular Laplas o'zgarishi kabi narsa borligini eslashadi. O'z-o'zidan bu bir kilogramm mayiz emas. Radiotexnikada bunga yo'l qo'yilishining yagona sababi shundaki, bu o'zgarish o'tish bo'lgan argument maydonida ba'zi narsalar aslida soddalashadi. Xususan, vaqt domenida bizga juda ko'p muammo tug'dirgan bir xil delta funktsiyasi juda oson ifodalangan - bu faqat bitta!
Z-transformatsiyasi (aka Laurent transformatsiyasi) diskret tizimlar uchun Laplas transformatsiyasining versiyasidir.
Ya'ni, kerakli filtrni tavsiflovchi funktsiyaga Laplas konvertatsiyasini (yoki kerak bo'lganda Z-transformatsiyasini) qo'llash, natijada olingan filtrni almashtirish va orqaga aylantirish orqali biz impuls javobini olamiz. Bu oson tuyuladi, har kim sinab ko'rishi mumkin. Men buni xavf ostiga qo'ymayman, chunki yuqorida aytib o'tilganidek, Laplas konvertatsiyasi qattiq narsa, ayniqsa teskari. Keling, buni oxirgi chora sifatida qoldiraylik va biz izlayotgan narsaga erishishning oddiyroq usullarini qidiramiz. Ulardan bir nechtasi bor.
Birinchidan, tabiatning yana bir hayratlanarli faktini eslashimiz mumkin - amplituda-chastota va impuls xususiyatlari bir-biri bilan yaxshi va tanish Furye konvertatsiyasi bilan bog'liq. Bu shuni anglatadiki, biz o'z didimizga qarab har qanday chastota reaktsiyasini chizishimiz, undan teskari Furye konvertatsiyasini olishimiz (uzluksiz yoki diskret) va uni amalga oshiradigan tizimning impulsli javobini olishimiz mumkin. Bu shunchaki ajoyib!
Biroq, bu muammosiz bo'lmaydi. Birinchidan, biz oladigan impuls reaktsiyasi cheksiz bo'lishi mumkin (nima uchun tushuntirishlarga kirmayman; dunyo shunday ishlaydi), shuning uchun biz bir nuqtada uni to'xtatish uchun ixtiyoriy qaror qabul qilishimiz kerak (sozlash) bu nuqtadan keyin nolga teng). Ammo bu xuddi shunday bo'lmaydi - buning oqibati, kutilganidek, hisoblangan filtrning chastota reaktsiyasining buzilishi bo'ladi - u to'lqinli bo'ladi va chastotani kesish xiralashadi.
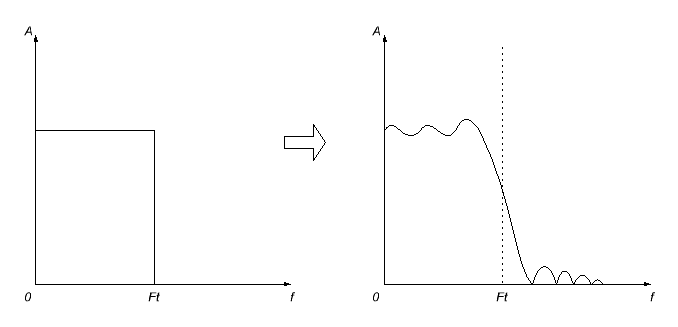
Ushbu effektlarni minimallashtirish uchun qisqartirilgan impuls javobiga turli yumshatuvchi oyna funksiyalari qo'llaniladi. Natijada, chastota reaktsiyasi odatda yanada xiralashadi, lekin yoqimsiz (ayniqsa, o'tish bandida) tebranishlar yo'qoladi. 
Aslida, bunday ishlov berishdan so'ng biz ishlaydigan impuls javobini olamiz va raqamli filtrni qurishimiz mumkin.
Ikkinchi hisoblash usuli yanada sodda - eng mashhur filtrlarning impulsli javoblari biz uchun uzoq vaqtdan beri analitik shaklda ifodalangan. Qolgan narsa sizning qiymatlaringizni almashtirish va natijaga o'zingizning xohishingizga ko'ra oyna funktsiyasini qo'llashdir. Shunday qilib, siz hech qanday o'zgarishlarni hisobga olishingiz shart emas.
Va, albatta, agar maqsad ma'lum bir sxemaning xatti-harakatlariga taqlid qilish bo'lsa, simulyatorda uning impulsli javobini olishingiz mumkin:
Bu erda men RC pallasining kirishiga 1 mks davomiylikdagi 100500 volt (ha, 100,5 kV) impulsni qo'lladim va uning impulsli javobini oldim. Buni haqiqatda amalga oshirish mumkin emasligi aniq, lekin simulyatorda bu usul, ko'rib turganingizdek, ajoyib ishlaydi.
5. Eslatmalar.
Impulsli javobni qisqartirish haqida yuqorida aytilgan narsa, albatta, so'zda qo'llaniladi. chekli impulsli javob filtrlari (FIR/FIR filtrlari). Ular bir qator qimmatli xususiyatlarga ega, shu jumladan chiziqli faza (impuls javobini yaratish uchun ma'lum sharoitlarda), bu filtrlash paytida signal buzilishining yo'qligini, shuningdek mutlaq barqarorlikni ta'minlaydi. Bundan tashqari, cheksiz impulsli javob filtrlari (IIR/IIR filtrlari) mavjud. Ular hisob-kitoblar nuqtai nazaridan kamroq resurs talab qiladi, lekin endi sanab o'tilgan afzalliklarga ega emas.
Keyingi maqolada raqamli filtrni amaliy qo'llashning oddiy misolini ko'rib chiqmoqchiman.
NOVOSIBIRSK DAVLAT TEXNIK UNIVERSITETI
AVTOMATIKA VA KOMPYUTER TEXNIKSIYASI FAKULTETI
Ma'lumotlarni yig'ish va qayta ishlash tizimlari bo'limi
"Nazariya va signalni qayta ishlash" intizomi
LABORATORIYA ISHI №.10
RAQAMLI FILTRLAR
CHEKLI IMPULS XUSUSIYATLARI BILAN
Guruh: AT-33
Variant: 1 O'qituvchi:
Talaba: Shadrina A.V. Dots. Shchetinin Yu.I.
Ishning maqsadi: yumshatuvchi oyna funksiyalaridan foydalangan holda chekli impulsli javob filtrlarini tahlil qilish va sintez qilish usullarini o'rganish.
Ishni yakunlash:
1. Filtr uzunligi va qiymatlari uchun to'rtburchaklar oynali kesish chastotasiga ega past o'tkazuvchan FIR filtrining impuls javob sxemalari.
Ideal diskret FIR filtrining impuls javobi cheksiz uzunlikka ega va ning salbiy qiymatlari uchun nolga teng emas:
.
Jismoniy jihatdan mumkin bo'lgan filtrni olish uchun impuls javobini cheklangan songa cheklash kerak, so'ngra kesilgan javobni o'ngga bir miqdorga siljitish kerak.
Qiymat - filtrning uzunligi (o'lchami), 
- filtrlash tartibi.
Matlab skripti (labrab101.m)
N = input("N filtr uzunligini kiriting = ");
h = sin(wc.*(n-(N-1)/2))./(pi.*(n-(N-1)/2));
xlabel("Ma'lumot raqami, n")
>> pastki chizma (2,1,1)
>> labrab101
Filtr uzunligini N = 15 kiriting
>> sarlavha ("N=15 uchun FIR filtrining impuls javobi")
>> pastki chizma (2,1,2)
>> labrab101
Filtr uzunligini N = 50 kiriting
>> sarlavha ("N=50 uchun FIR filtrining impuls javobi")
1-rasm. Filtr uzunligi va qiymatlari uchun to'rtburchaklar oynali kesish chastotasiga ega past o'tkazuvchan FIR filtrining impulsli javob sxemalari.
Izoh: Agar raqamli filtrning chastotali javobini Furye seriyasi deb hisoblasak: 
, keyin ushbu seriyaning koeffitsientlari filtrning impuls javobining qiymatlarini ifodalaydi. Bunday holda, Furye seriyasi birinchi holatda - ga, ikkinchisida - ga qisqartirildi, keyin esa kesilgan xarakteristikalar sabab filtrini olish uchun namuna o'qi bo'ylab o'ngga siljidi. Asosiy lobning kengligi 2 bo'lsa, va qachon - 1, ya'ni. Filtr uzunligi oshgani sayin, impuls javobining asosiy lobi torayadi. Agar yon bo'laklarning darajasini hisobga oladigan bo'lsak (foydalanish ), keyin ortishi bilan u mutlaq qiymatdan dan gacha ortadi. Shunday qilib, biz to'rtburchaklar oynali filtrning ideal chastota ta'sirini taxmin qilishdan foydalanganda, bir vaqtning o'zida asosiy bo'lakni toraytirish (va shu bilan o'tish hududini kamaytirish) va yon bo'laklarning darajasini kamaytirish (kamaytirish) mumkin emas degan xulosaga kelishimiz mumkin. filtrning o'tish va to'xtash bandidagi dalgalanma). To'rtburchak oynaning yagona boshqariladigan parametri uning o'lchamidir, uning yordamida siz asosiy lobning kengligiga ta'sir qilishingiz mumkin, ammo u yon bo'laklarga unchalik ta'sir qilmaydi.
2. Funktsiya yordamida 1-bosqichdan impuls xarakteristikasining DVFT ni hisoblash. Chiziqli miqyosda va desibellarda ularning chastota ta'sirining grafiklari 512 chastota namunalari. Filtrning o'tish diapazoni, o'tish bandi va to'xtash bandi. Filtr tartibining o'tish diapazoni kengligiga va o'tish va to'xtash diapazonlarida chastotaga ta'sir qilish darajasiga ta'siri.
Matlab funktsiyasi (DTFT.m)
funktsiya = DTFT(x,M)
N = max(M, uzunlik(x));
% FFT hajmini 2^m gacha kamaytirish
N = 2^(cheil(log(N)/log(2))));
% Fftni hisoblang
% Chastotalar vektori
w = 2*pi*((0:(N-1))/N);
w = w - 2*pi*(w>=pi);
% FFT-ni -pi dan +pi oralig'iga o'tkazing
X = fftshift (X);
w = fftshift(w);
Matlab skripti (labrab102.m)
h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));
h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));
DTFT (h1,512);
DTFT (h2,512);
chizma(w./(2*pi),abs(H1)./maks(abs(H1)),"r")
xlabel("f, Hz"), ylabel("|H1|/max(|H1|)"), panjara
chizma (w./(2*pi), abs(H2)./maks (abs(H2)), "b")
xlabel("f, Hz"), ylabel("|H2|/max(|H2|)"), panjara
chizma(w./(2*pi),20*log10(abs(H1)),"r")
title("N = 15 uchun to'rtburchaklar oynali past chastotali FIR filtrining chastotali javobi")
xlabel("f, Hz"), ylabel("20lg(|H1|), dB"), panjara
chizma(w./(2*pi),20*log10(abs(H2)),"b")
title("N = 50 uchun to'rtburchaklar oynali past chastotali FIR filtrining chastotali javobi")
xlabel("f, Hz"), ylabel("20lg(|H2|), dB"), panjara
2-rasm. Filtr uzunligi qiymatlari va chiziqli shkala bo'yicha to'rtburchaklar oynali kesish chastotasi bilan past o'tkazuvchan FIR filtrining chastotali javob sxemalari
3-rasm. Filtr uzunligi qiymatlari va logarifmik shkala bo'yicha to'rtburchaklar oynali kesish chastotasi bilan past o'tkazuvchan FIR filtrining chastotali javob sxemalari
Izoh:
1-jadval. O'tish diapazoni, o'tish hududi va filtr uzunligi uchun to'xtash chizig'i va
|
Filtr uzunligi |
Tarmoqli kengligi, Hz |
O'tish hududi, Hz |
To'xtash diapazoni, Hz |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
10-sonli ma’ruza "Cheklangan impulsli javobli raqamli filtrlar" Jismoniy jihatdan amalga oshiriladigan raqamli chekli impuls javob filtrining (FIR filtri) uzatish funktsiyasi quyidagicha ifodalanishi mumkin. (10.1). (10.1) ifodani almashtirishda biz FIR filtrining chastotali javobini shaklda olamiz Qayerda Faza kechikishi filtr sifatida aniqlanadi Guruh kechikishi filtr sifatida aniqlanadi FIR filtrlarining o'ziga xos xususiyati doimiy faza va guruh kechikishlarini amalga oshirish qobiliyatidir, ya'ni. chiziqli fazali javob (10.5), qayerda a - doimiy. Agar bu shart bajarilsa, filtrdan o'tadigan signal uning shaklini buzmaydi. Chiziqli fazaviy javobni ta'minlaydigan shartlarni olish uchun biz (10.5) ni hisobga olgan holda FIR filtrining chastotali javobini yozamiz. Ushbu tenglikning haqiqiy va xayoliy qismlarini tenglashtirib, biz olamiz Ikkinchi tenglamani birinchisiga bo'lib, biz olamiz Nihoyat, biz yozishimiz mumkin Bu tenglama ikkita yechimga ega. Birinchi qachon a =0 tenglamaga mos keladi Bu tenglama ixtiyoriyga mos keladigan yagona yechimga ega h (0) (sin (0)=0), va n uchun h (n)=0 >0. Ushbu yechim impuls javobi dastlabki vaqtda bitta nolga teng bo'lmagan namunaga ega bo'lgan filtrga mos keladi. Bunday filtr amaliy qiziqish uyg'otmaydi. uchun boshqa yechim topamiz. Bunda (10.8) son va maxrajlarni o‘zaro ko‘paytirsak, hosil bo‘ladi. (10.11). Bu yerdan biz bor Ushbu tenglama Furye qatori ko'rinishiga ega bo'lganligi sababli, uning yechimi, agar mavjud bo'lsa, yagonadir. Bu tenglamaning yechimi shartlarni qondirishi kerakligini tushunish oson (10.13), (10.14). (10.13) shartdan kelib chiqadiki, har bir filtr tartibi uchun N faqat bitta fazali kechikish mavjud a , bunda fazaviy javobning qat'iy chiziqliligiga erishish mumkin. (10.14) shartdan kelib chiqadiki, filtrning impulsli javobi toq nuqtaga nisbatan simmetrik bo'lishi kerak. N , va intervalning o'rta nuqtasiga nisbatan (10.1-rasm).
Bunday filtrning chastotali javobi (g'alati uchun N ) shaklida yozilishi mumkin (10.15). Ikkinchi miqdorda almashtirishni amalga oshirish m = N -1- n, biz olamiz (10.16). Chunki h (n)= h (N -1- n ), keyin ikkita summani birlashtirish mumkin ni almashtirsak, olamiz (10.18). Agar belgilasak keyin biz nihoyat yozishimiz mumkin Shunday qilib, chiziqli fazali javobga ega filtr uchun bizda mavjud Juft holati uchun N xuddi shunday bo'lamiz Ikkinchi summada almashtirishni amalga oshirsak, biz olamiz O'zgartirishni amalga oshirsak, biz olamiz (10.24). Belgilangan holda biz nihoyat ega bo'lamiz Shunday qilib, chiziqli fazali javob va hatto tartib bilan FIR filtri uchun N yozish mumkin Keyinchalik, soddaligi uchun biz faqat g'alati tartibli filtrlarni ko'rib chiqamiz. Filtrni uzatish funktsiyasini sintez qilishda dastlabki parametrlar, qoida tariqasida, chastota javobiga qo'yiladigan talablardir. FIR filtrlarini sintez qilishning ko'plab usullari mavjud. Keling, ulardan ba'zilarini ko'rib chiqaylik. Har qanday raqamli filtrning chastota reaktsiyasi chastotaning davriy funktsiyasi bo'lganligi sababli, uni Furye seriyasi sifatida ko'rsatish mumkin. bu erda Furye qatorining koeffitsientlari teng Ko'rinib turibdiki, Furye qatorining koeffitsientlari h(n ) filtrning impulsga javob koeffitsientlari bilan mos keladi. Shuning uchun filtrning zarur chastotali javobining analitik tavsifi ma'lum bo'lsa, unda impuls ta'sirining koeffitsientlarini va ulardan filtrning uzatish funktsiyasini osongina aniqlash mumkin. Biroq, amalda buni amalga oshirish mumkin emas, chunki bunday filtrning impulsli javobi cheksiz uzunlikka ega. Bundan tashqari, bunday filtrni jismonan amalga oshirish mumkin emas, chunki impuls javobi boshlanadi -¥ , va hech qanday chekli kechikish bu filtrni jismoniy amalga oshirishga imkon bermaydi. Berilgan chastotali javobga yaqin bo'lgan FIR filtrini olishning mumkin bo'lgan usullaridan biri bu cheksiz Furye seriyasini va filtrning impuls javobini qisqartirishdir. h (n)=0 da. Keyin O'tkazish funktsiyasining jismoniy amalga oshirilishi H(z ) ko‘paytirish orqali erishish mumkin H(z) yoqilgan. Qayerda (10.32). O'tkazish funktsiyasining bunday o'zgarishi bilan filtrning amplitudali xarakteristikasi o'zgarmaydi va guruhning kechikishi doimiy miqdorda ortadi. Misol tariqasida, shaklning chastotali javobi bilan past chastotali FIR filtrini hisoblaylik (10.29) ga muvofiq, filtr impulslarining javob koeffitsientlari ifoda bilan tavsiflanadi Endi (10.31) dan biz uzatish funksiyasi uchun ifodani olishimiz mumkin Qayerda (10.36). Turli xillar uchun hisoblangan filtrning amplitudali xarakteristikalari N 10.2-rasmda keltirilgan.
10.2-rasm O'tish va to'xtash diapazonidagi to'lqinlanish Furye seriyasining sekin yaqinlashuvi tufayli yuzaga keladi, bu esa, o'z navbatida, o'tish diapazoni kesish chastotasida funktsiyada uzilish mavjudligidan kelib chiqadi. Bu pulsatsiyalar deb nomlanadi Gibbs to'lqinlanadi. 10.2-rasmdan ko'rinib turibdiki, ortib borishi bilan N pulsatsiya chastotasi ortadi va amplituda past va yuqori chastotalarda kamayadi. Shu bilan birga, o'tish chizig'idagi oxirgi to'lqinning amplitudasi va to'xtash chizig'idagi birinchi dalgalanma amalda o'zgarishsiz qoladi. Amalda, bunday ta'sirlar ko'pincha istalmagan bo'lib, bu Gibbs pulsatsiyasini kamaytirish yo'llarini topishni talab qiladi. Qisqartirilgan impulsli javob h(n ) talab qilinadigan cheksiz impuls javobining mahsuloti va ba'zilari sifatida ifodalanishi mumkin oyna funktsiyalari n uzunlikdagi w (n) (10.3-rasm).
Furye seriyasini oddiy qisqartirishning ko'rib chiqilayotgan holatida biz foydalanamiz to'rtburchak oyna Bunday holda, filtrning chastotali javobi murakkab konvolyutsiya sifatida ifodalanishi mumkin Bu shuni anglatadiki, u talab qilinadigan xarakteristikaning "loyqa" versiyasi bo'ladi. Muammo Gibbs to'lqinini bir xil filtr selektivligi bilan kamaytirishga imkon beradigan oyna funksiyalarini topishga to'g'ri keladi. Buning uchun, avvalo, to'rtburchak oyna misolidan foydalanib, oyna funksiyasining xususiyatlarini o'rganishingiz kerak. To'rtburchak oyna funksiyasining spektri quyidagicha yozilishi mumkin To'rtburchak oyna funksiyasining spektri 10.4-rasmda keltirilgan.
10.4-rasm dan boshlab spektrning asosiy bo'lagining kengligi ga teng bo'lib chiqadi. Oyna funksiyasining spektrida yon loblarning mavjudligi filtrning chastotali javobida Gibbs to'lqinining oshishiga olib keladi. O'tish chizig'ida past to'lqinlanish va to'xtash chizig'ida yuqori zaiflashishni olish uchun yon bo'laklar bilan chegaralangan maydon asosiy bo'lak bilan cheklangan maydonning kichik bir qismi bo'lishi kerak. O'z navbatida, asosiy lobning kengligi olingan filtrning o'tish zonasining kengligini aniqlaydi. Yuqori filtr selektivligi uchun asosiy lobning kengligi imkon qadar kichik bo'lishi kerak. Yuqoridagilardan ko'rinib turibdiki, asosiy lobning kengligi ortib borayotgan filtrlash tartibi bilan kamayadi. Shunday qilib, mos oyna funktsiyalarining xususiyatlarini quyidagicha shakllantirish mumkin: - oyna funktsiyasi vaqt bilan cheklanishi kerak; - oyna funksiyasining spektri chastota bilan cheklangan funksiyaga eng yaqin bo'lishi kerak, ya'ni. asosiy lobdan tashqarida minimal energiyaga ega bo'lish; - Oyna funksiyasi spektrining asosiy lobining kengligi imkon qadar kichik bo'lishi kerak. Eng ko'p ishlatiladigan oyna funktsiyalari: 1. To'rtburchak oyna. Yuqorida muhokama qilingan. 2. Hamming oynasi. Qayerda. Bu oyna Hann oynasi deb ataladi ( hanning). 3. Blackman oynasi. 4. Bartlettning oynasi. Belgilangan oyna funksiyalari yordamida qurilgan filtrlarning ko'rsatkichlari 10.1-jadvalda jamlangan.
Dalgalanish omili oyna funktsiyasi spektrida yon lobning maksimal amplitudasining asosiy lobning amplitudasiga nisbati sifatida aniqlanadi. Haqiqiy filtrlarni hisoblashda kerakli filtr tartibini va eng mos oyna funksiyasini tanlash uchun 10.2-jadvaldagi ma'lumotlardan foydalanish mumkin.
10.1-jadvaldan ko'rinib turibdiki, oyna funktsiyasi spektrida to'lqinlanish koeffitsienti va asosiy lobning kengligi o'rtasida ma'lum bir bog'liqlik mavjud. Pulsatsiya koeffitsienti qanchalik kichik bo'lsa, asosiy lobning kengligi va shuning uchun filtrning chastotali javobidagi o'tish zonasi. O'tish chizig'ida past to'lqinlanishni ta'minlash uchun mos keladigan dalgalanma koeffitsientiga ega oynani tanlash va o'tish zonasining kerakli kengligini N filtrlash tartibini oshirish kerak. Bu muammoni Kaiser tomonidan taklif qilingan oyna yordamida hal qilish mumkin. Kaiser oynasi funksiyasi formaga ega
bu erda a mustaqil parametr,
Kaiser oynasining jozibali xususiyati pulsatsiya koeffitsientini kichik qiymatlardan katta qiymatlarga silliq o'zgartirish qobiliyatidir, bunda faqat bitta parametr a o'zgaradi. Bu holda, oynaning boshqa funktsiyalarida bo'lgani kabi, asosiy lobning kengligi N filtr tartibi bilan sozlanishi mumkin. Haqiqiy filtrni ishlab chiqishda o'rnatiladigan asosiy parametrlar: Tarmoqli kengligi - w p; To'siq chizig'i - w a ; O'tish chizig'idagi maksimal ruxsat etilgan dalgalanma A p; Minimal to'xtash chizig'ining susayishi - A a; -namuna olish chastotasi - ws. Bu parametrlar 10.5-rasmda tasvirlangan. Bunday holda, o'tish chizig'idagi maksimal dalgalanma sifatida aniqlanadi
va to'xtash bandidagi minimal zaiflashuv quyidagicha Kaiser oynasi bilan filtrni hisoblashning nisbatan oddiy tartibi quyidagi bosqichlarni o'z ichiga oladi: 1. Chastota javobi ideal bo'lishi sharti bilan h (n) filtrining impuls javobi aniqlanadi
qaerda (10.49). 2. d parametri sifatida tanlanadi
Qayerda 3. A a va A p ning haqiqiy qiymati (10.46), (10.47) formulalar yordamida hisoblanadi. 4. a parametri sifatida tanlanadi
5. D parametri sifatida tanlanadi
6. Shartdan filtr tartibining eng kichik toq qiymatini tanlang
shunga amal qiladi Filtrning impulsli javob namunalari uning uzatish funktsiyasining koeffitsientlari bo'lganligi sababli (10.59) shart barcha filtr koeffitsientlarining kodlari faqat kasr qismi va ishora bitini o'z ichiga oladi va butun sonni o'z ichiga olmaydi. Filtr koeffitsientlarining kasr qismining raqamlari soni filtr o'tkazish funktsiyasini kvantlangan koeffitsientlar bilan qondirish sharti, koeffitsientlarning aniq qiymatlari bilan mos yozuvlar uzatish funktsiyasiga yaqinlashish uchun belgilangan talablar asosida aniqlanadi. Filtrning kirish signali namunalarining mutlaq qiymatlari odatda shunday normallashtiriladi Agar tahlil chiziqli fazali javobga ega FIR filtri uchun o'tkazilsa, uning chiqish signalini hisoblash algoritmi quyidagicha bo'lishi mumkin. qayerda filtr koeffitsientlari s k ga yaxlitlangan. Bu algoritm 10.5-rasmda ko'rsatilgan filtr blok sxemasiga mos keladi.
Ushbu algoritmni amalga oshirishning ikki yo'li mavjud. Birinchi holda, barcha ko'paytirish operatsiyalari aniq bajariladi va mahsulotlarni yaxlitlash yo'q. Bunday holda, mahsulotlarning bit chuqurligi s in +s k ga teng, bu erda s in - kirish signalining bit chuqurligi va s k - filtr koeffitsientlarining bit chuqurligi. Bunday holda, 10.5-rasmda ko'rsatilgan filtrning blok sxemasi haqiqiy filtrga to'liq mos keladi. Algoritmni amalga oshirishning ikkinchi usulida (10.61) ko'paytirish operatsiyasining har bir natijasi yaxlitlanadi, ya'ni. mahsulotlar ba'zi xatolar bilan hisoblanadi. Bunday holda, mahsulotlarni yaxlitlash orqali kiritilgan xatoni hisobga olish uchun algoritmni (10.61) o'zgartirish kerak. Agar filtr chiqish signalining namunaviy qiymatlari birinchi usul (mahsulotlarning aniq qiymatlari bilan) yordamida hisoblansa, chiqish shovqinining tarqalishi quyidagicha aniqlanadi.
bular. kirish signalining yaxlitlash shovqinining o'zgarishiga va filtr koeffitsientlarining qiymatlariga bog'liq. Bu yerdan kirish signalining kerakli bit sonini sifatida topishingiz mumkin
s in va s k ning ma'lum qiymatlaridan foydalanib, chiqish signali kodining kasr qismi uchun zarur bo'lgan bitlar sonini aniqlash mumkin: Agar chiqish signali namunalarining qiymatlari ikkinchi usul yordamida hisoblansa, har bir mahsulot s d raqamlariga yaxlitlanganda, ko'paytirgichlarning har biri tomonidan yaratilgan yaxlitlash shovqinining dispersiyasi raqam sig'imi bilan ifodalanishi mumkin. sifatida mahsulot DR kirish va SNR chiqishi filtrida signal-shovqin nisbati. Desibellardagi kirish signalining dinamik diapazoni quyidagicha aniqlanadi
bu erda A max va A min - filtr kirish signalining maksimal va minimal amplitudalari. Desibellarda ifodalangan filtr chiqishidagi signal-shovqin nisbati quyidagicha aniqlanadi
A min amplitudali filtrning chiqish sinusoidal signali kuchining o'rtacha kvadrat qiymatini aniqlaydi va (10.77) filtr chiqishidagi shovqin kuchini aniqlaydi. (10.75) va (10.76) dan A max =1 bilan filtr chiqish shovqinining dispersiyasi ifodasini olamiz. Ushbu filtr chiqish shovqin dispersiyasi qiymati filtrning kirish va chiqish signallarining bit chuqurligini hisoblash uchun ishlatilishi mumkin.  Bepul dasturlar va foydali maslahatlar dunyosi 2024 whatsappss.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(10.2),
- amplituda chastotali javob (AFC) filtr,
- fazali chastotali javob (PFC) filtr.
(10.3).
(10.4).
(10.6).
(10.7).
(10.8).
(10.9).
(10.10).
(10.12).
(10.17).
(10.19),
(10.20).
(10.21).
(10.22).
(10.23).
(10.25),
(10.26).
(10.27).
(10.28),
(10.29).
(10.30).
(10.31),
(10.33).
(10.34).
(10.35),
(10.37).
(10.38).
(10.39).
(10.40).
(10.41),
(10.42).
(10.43).
(10.44),
, I 0 – ifoda bilan aniqlangan birinchi turdagi nol tartibli Bessel funksiyasi
(10.45).
(10.46),
(10.50),
(10.51).
(10.52).
(10.53).
(10.54),
(10.57)
(10.66),
(10.67).
(10.74),
(10.75),
(10.78).