Impulssvar från filtret. Digitala filter med ändlig impulsrespons. Datautjämning. Medianfiltrering
48 Digitala filter med ändlig impulsrespons. Beräkning av kih-filter.
Finita Impulse Response Filter (Icke-rekursivt filter, FIR-filter) eller FIR-filter (FIR förkortas från finite impulse response - finite impulse response) - en av typerna av linjära digitala filter, vars kännetecknande är dess tidsbegränsning impulsivt svar(från någon tidpunkt blir det exakt lika med noll). Ett sådant filter kallas även icke-rekursivt på grund av bristen på återkoppling. Nämnaren för överföringsfunktionen för ett sådant filter är en viss konstant.
Differensekvation som beskriver förhållandet mellan filtrets in- och utsignaler: där P- filterordning, x(n) - ingångssignal, y(n) är utsignalen, och b i- filterkoefficienter. Med andra ord bestäms värdet för varje utsignalssampel av summan av de skalade värdena P tidigare avläsningar. Du kan säga det annorlunda: värdet på filterutgången när som helst är värdet av svaret på det momentana värdet av ingången och summan av alla gradvis avklingande svar P tidigare signalsampel som fortfarande påverkar utsignalen (efter P-räknas, blir pulsövergångsfunktionen lika med noll, som redan nämnts, därför alla termer efter P-th blir också lika med noll). Låt oss skriva den föregående ekvationen i en mer rymlig form:
För att hitta filterkärnan lägger vi
x(n) = δ( n)
där δ( n) - deltafunktion. Då kan FIR-filtrets impulssvar skrivas som:
Z-transformeringen av impulssvaret ger oss överföringsfunktionen för FIR-filtret:
]Egenskaper
FIR-filtret har ett antal användbara egenskaper som gör att det ibland är bättre att använda än ett IIR-filter. Här är några av dem:
FIR-filter är robusta.
FIR-filter kräver ingen återkoppling när de implementeras.
Fasen för FIR-filter kan göras linjär
Direkt form av FIR-filter
FIR-filter kan implementeras med hjälp av tre element: en multiplikator, en adderare och ett fördröjningsblock. Alternativet som visas i figuren är en direkt implementering av typ 1 FIR-filter.
Implementering av den direkta formen av FIR-filtret
Exempel på program
Nedan är ett exempel på ett FIR-filterprogram skrivet i C:
/* FIR-filter för 128 kranar */
float fir_filter(float input)
statiskt flytprov;
acc = 0,0f; /* Batteri */
/* Multiplicera och ackumulera */
för (i = 0; i< 128; i++) {
acc += (h[i] * prov[i]);
/* Utgång */
/* Skift den fördröjda signalen */
för (i = 127; i > 0; i--)
prov[i] = prov;
49 Datautjämning. Rörliga medelvärde.
50 Datautjämning. Parabolisk utjämning.
51 Datautjämning. Spencer utjämning.
52 Datautjämning. Medianfiltrering.
Rörligt medelvärde, parabolisk utjämning, Spencer-utjämning, medianfiltrering
När man utvecklar metoder för att bestämma parametrarna för fysiska processer som långsamt förändras över tiden, är en viktig uppgift att eliminera påverkan av bruseffekter eller slumpmässiga störningar som överlagras på den behandlade signalen som tas emot vid utgången av den primära omvandlaren.
För att eliminera denna effekt kan du använda datautjämning. En av de enklaste metoderna för sådan utjämning är aritmetiskt medelvärde. När du använder den beräknas varje värde för en diskret funktion (array med bearbetad data) i enlighet med uttrycket:
där är antalet poäng för aritmetisk medelvärdesberäkning (udda heltal);
Funktionens värde före bearbetning;
Det finns andra ganska effektiva metoder för utjämning, till exempel med paraboler av andra graden på fem, sju, nio och elva punkter i enlighet med uttrycken:
eller paraboler av fjärde graden vid sju, nio, elva och tretton poäng:
I praktiska tillämpningar ger andra effektiva metoder, till exempel 15-punkts Spencer-utjämning, bra resultat:
Genom att ersätta den komplexa exponentialen , där i dessa uttryck, kan vi bestämma överföringsfunktionen för motsvarande transformation.
För aritmetiskt medelvärde
Uttrycket inom parentes representerar en geometrisk progression med en nämnare, därför kan detta uttryck representeras som:
.
Denna formel representerar överföringskarakteristiken för ett lågpassfilter och den visar att ju fler termer som är involverade i medelvärdesbildning, desto större undertryckning av högfrekventa bruskomponenter i signalen (se figur 6.1).
Det semantiska konceptet med frekvens vid behandling av tidstrender skiljer sig dock från ett liknande koncept vid behandling av signaler. Detta förklaras av det faktum att när man studerar tidstrender är det inte deras frekvenssammansättning som är av intresse, utan typen av förändring (ökning, minskning, konstans, cyklicitet, etc.).
Användningen av så kallade heuristiska algoritmer är också ganska effektiv för att utjämna data.
En av dem är medianfiltrering. Under dess implementering i ett glidande tidsfönster av dimension , där heltal är ett udda tal, ersätts det centrala elementet av mittelementet i sekvensen, som är ordnade, i stigande ordning av värden, element i datamatrisen för den utjämnade signal som faller inom tidsfönstret. Fördelen med medianfiltrering är möjligheten att ta bort impulsbrus, vars varaktighet inte överstiger, med praktiskt taget ingen distorsion av jämnt varierande signaler. Denna metod för brusreducering har inte en strikt matematisk motivering, men enkelheten i beräkningar och effektiviteten av de erhållna resultaten har lett till att den används i stor utsträckning.
Figur 6.1 - Överföringskarakteristiska grafer
aritmetiska medelvärdesoperationer för m=5, 7, 9, 11
En annan intressant utjämningsalgoritm är mediangenomsnitt. Dess väsen är som följer. I ett glidande tidsfönster av storlek (-udda heltal), ordnas elementen i datamatrisen i stigande ordning, och sedan tas de första och sista elementen bort från den ordnade sekvensen (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
Denna metod låter dig undertrycka puls- och radiofrekvensstörningar, samt uppnå god signalutjämning.
| " |
Låt oss överväga det enklaste av digitala filter - filter med konstanta parametrar.
Ingångssignalen från det digitala filtret tillförs i form av en sekvens av numeriska värden som följer med intervaller (Fig. 4.1, a). När varje nästa signalvärde tas emot i det digitala filtret, beräknas nästa värde på utsignalen.Beräkningsalgoritmer kan vara mycket olika; under beräkningsprocessen, förutom det sista värdet på insignalen, kan användas
tidigare värden för in- och utsignalerna: Utsignalen från ett digitalt filter är också en sekvens av numeriska värden som följer ett intervall på . Detta intervall är detsamma för hela den digitala signalbehandlingsenheten.
Ris. 4.1. Signal vid digitalfiltrets ingång och utgång
Därför, om du applicerar den enklaste signalen i form av en enda puls till ingången till ett digitalt filter (Fig. 4.2, a)
då får vi vid utgången en signal i form av en diskret sekvens av numeriska värden, som följer med intervaller
I analogi med konventionella analoga kretsar kommer vi att kalla denna svarssignal för filtrets impulssvar (Fig. 4.2, b). Till skillnad från impulssvaret hos en analog krets är funktionen dimensionslös.
Ris. 4.2. Enhetsimpuls och impulssvar för ett digitalt filter
Låt oss applicera en godtycklig diskret signal till filteringången (Fig. 4.1, a), som är en uppsättning diskreta värden
Under verkan av det första elementet bildas en sekvens multiplicerad med vid utgången av filtret, under åtgärden multipliceras en sekvens med och skiftas åt höger med ett belopp, etc. Som ett resultat kommer utgången att få sekvens var
Sålunda definieras utsignalen som den diskreta faltningen av insignalen och impulssvaret. I detta avseende liknar digitala filter konventionella kretsar, där utsignalen är lika med faltningen av insignalen och impulssvaret.
Formel (4.1) är en digital filtreringsalgoritm. Om impulssvaret för ett filter beskrivs av en sekvens med ett ändligt antal termer, kan filtret implementeras i form av en krets som visas i fig. 4.3. Här indikerar bokstaven elementen för signalfördröjning för tid (per cell); -element som multiplicerar signalen med motsvarande koefficient.
Diagrammet som visas i fig. 4.3 är inte en elektrisk krets för ett digitalt filter; Detta diagram är en grafisk representation av den digitala filtreringsalgoritmen och visar sekvensen av aritmetiska operationer som utförs under signalbehandling.
Ris. 4.3. Icke-rekursiv digital filterkrets
För digitala filter som behandlar signaler i form av abstrakta numeriska sekvenser är begreppet ”tidsfördröjning” inte helt korrekt. Därför är element som fördröjer signalen med en cell vanligtvis markerade på digitala filterkretsar med en symbol som indikerar signalfördröjningen på språket -transformationer. I det följande kommer vi att hålla oss till denna notation.
Låt oss återgå till den digitala filterkretsen som visas i fig. 4.3, Sådana filter, där endast värdena på ingångssignalen används för beräkning, kallas enkla eller icke-rekursiva.
Den icke-rekursiva filteralgoritmen är lätt att skriva om filtrets impulssvar är känt. För den praktiska implementeringen av algoritmen är det nödvändigt att impulssvaret innehåller ett ändligt antal termer. Om impulssvaret innehåller ett oändligt antal termer, men de snabbt minskar i värde, kan du begränsa dig till ett begränsat antal termer och kasta bort de vars värden är små. Om elementen i impulssvaret inte minskar i värde, visar sig den icke-rekursiva filteralgoritmen vara orealiserbar.
Ris. 4.4. -kedja
Som ett exempel, betrakta det enklaste digitala filtret, liknande -kretsen (Fig. 4.4). Kretsens impulssvar har formen
För att skriva impulssvaret för det motsvarande digitala filtret bör uttrycket ersättas med Emellertid har impulssvaret för en krets en dimension, och impulssvaret för ett digitalt filter måste vara dimensionslöst. Därför utelämnar vi multiplikatorn i uttrycket (4.2) och skriver impulssvaret för det digitala filtret i formen
Ett sådant impulssvar innehåller oändligt många termer, men deras storlek minskar enligt en exponentiell lag, och vi kan begränsa oss till termer genom att välja sådana att
Nu kan vi skriva uttrycket för signalen vid filterutgången
Detta uttryck är också en digital filteralgoritm. Diagrammet för detta filter visas i fig. 4.5.
Det andra tillvägagångssättet för att analysera processer i digitala filter liknar operatörsmetoden för att analysera konventionella analoga kretsar, men istället för Laplace-transformen används -transformen.
Ris. 4.5. Krets för ett icke-rekursivt digitalt filter liknande en -krets
Låt oss definiera en digital filterparameter som liknar överföringsfunktionen för en elektrisk krets. För att göra detta, tillämpa en transformation på impulssvaret för ett digitalt filter:
Funktionen kallas för systemfilterfunktionen.
I enlighet med uttryck (4.1) är signalen vid det digitala filtrets utgång lika med den diskreta faltningen av insignalen och filtrets impulssvar. Genom att tillämpa faltningssatsen på detta uttryck får vi att utsignaltransformationen är lika med insignaltransformationen multiplicerad med systemfilterfunktionen:
Således spelar systemfunktionen rollen som överföringsfunktionen för ett digitalt filter.
Som ett exempel, låt oss hitta systemfunktionen för ett första ordningens digitalt filter som liknar en -krets:
Den tredje metoden för att analysera passagen av signaler genom digitala filter liknar den klassiska metoden för differentialekvationer. Låt oss överväga denna metod med beställningskedjor som ett exempel.
Den enklaste analoga kretsen av 1:a ordningen är -kretsen (se fig. 4.4), vars passage av signaler beskrivs av differentialekvationen
För en diskret krets, istället för differentialekvationen (4.8), bör en skillnadsekvation skrivas, där in- och utsignalerna specificeras för diskreta tidpunkter, och istället för derivatan bör skillnaden mellan intilliggande signalvärden dyka upp. För en diskret 1:a ordningens krets kan differensekvationen skrivas i en ganska allmän form
Låt oss tillämpa transformationen på ekvationen
där vi hittar systemfilterfunktionen
Formel (4.10) är ett ganska allmänt uttryck för systemfunktionen hos ett 1:a ordningens digitalt filter. När det sammanfaller med det tidigare erhållna uttrycket (4.7) för systemfunktionen för ett digitalt filter ekvivalent med en -krets.
Låt oss hitta en digital filtreringsalgoritm som motsvarar systemfunktionen (4.10). För att göra detta löser vi ekvation (4.9) för
Ett ekvivalent diagram av denna algoritm visas i fig. 4.6. Jämfört med ett icke-rekursivt filter (se fig. 4.5) har här lagts till en slags "feedback-krets", vilket innebär att utsignalens värden används i efterföljande
Ris. 4.6. Krets av ett rekursivt digitalt filter liknande en -krets
beräkningar. Filter av denna typ kallas rekursiva.
Algoritm (4.11) motsvarar ett filter som är helt ekvivalent med det icke-rekursiva filtret som ansågs tidigare. Men för att bestämma ett värde på utsignalen med hjälp av den icke-rekursiva filteralgoritmen (4.4) är det nödvändigt att utföra operationer, och när du använder den rekursiva filteralgoritmen (4.11) krävs endast två operationer. Detta är den största fördelen med rekursiva filter. Dessutom tillåter rekursiva filter signalbehandling med högre noggrannhet, eftersom de tillåter en mer korrekt implementering av impulssvaret utan att kassera dess "svans". Rekursiva filter låter dig implementera algoritmer som inte alls kan implementeras med hjälp av icke-rekursiva filter. Till exempel, med ett filter som arbetar enligt kretsen i fig. 4.6, är i huvudsak en idealisk ackumulator-integrator och har ett impulssvar av formen Ett filter med en sådan egenskap kan inte implementeras med ett icke-rekursivt schema.
De övervägda exemplen visar att det inte är någon mening med att använda icke-rekursiva algoritmer för att skapa digitala filter med lång impulsrespons. I dessa fall är det lämpligare att använda rekursiva filter.
Tillämpningsområdet för icke-rekursiva algoritmer är implementeringen av digitala filter med ett impulssvar som innehåller ett litet antal termer. Ett exempel är den enklaste differentiatorn, vars utsignal är lika med ökningen av insignalen:
Kretsen för ett sådant digitalt filter visas i fig. 4.7.
Ris. 4.7. Krets för den enklaste digitala differentiatorn
Låt oss nu betrakta ett allmänt digitalt filter, som beskrivs av ekvationen
Denna ekvation kan betraktas både som en differensordningsekvation och som en digital filtreringsalgoritm, om den skrivs om annorlunda, nämligen
Ris. 4.8. Rekursiv digital ordningsfilterkrets
Algoritmen (4.13) motsvarar kretsen som visas i fig. 4.8. Låt oss hitta systemfunktionen för ett sådant filter. För att göra detta, tillämpa transformationen på ekvationen:
Uttryck (4.14) gör det möjligt för oss att upprätta en koppling mellan fluktuationerna hos elementen i filterkretsen och systemfunktionen. Koefficienterna i täljaren för systemfunktionen bestämmer värdena för koefficienterna för
(i den icke-rekursiva delen av filtret), och koefficienterna i nämnaren bestämmer den rekursiva delen av filtret.
Allt började när en vän till en vän till en vän behövde hjälp med samma filter. Genom Jedi-vägarna nådde rykten om detta mig, jag avslutade prenumerationen i kommentarerna till inlägget på länken. Det verkade hjälpa. Tja, hoppas jag.
Den här historien väckte minnen i mig från den tredje, eller något i stil med, förstås, när jag själv tog DSP:n och fick mig att skriva en artikel för alla som är intresserade av hur digitala filter fungerar, men som naturligtvis är rädda för över -the-top formler och psykedeliska teckningar i (jag redan jag pratar inte om läroböcker).
I allmänhet, enligt min erfarenhet, beskrivs situationen med läroböcker av den välkända frasen att man ibland inte kan se skogen för träden. Och det vill säga, när de omedelbart börjar skrämma dig med Z-transformen och formler för att dela polynom, som ofta är längre än två brädor, torkar intresset för ämnet extremt snabbt. Vi börjar med en enkel, lyckligtvis, för att förstå vad som händer, är det inte alls nödvändigt att beskriva långa komplexa uttryck.
Så först, några enkla grundbegrepp.
1. Impulssvar.
Låt oss säga att vi har en låda med fyra stift. Vi har ingen aning om vad som finns inuti, men vi vet med säkerhet att de två vänstra terminalerna är ingången och de två högra är utgången. Låt oss försöka applicera en mycket kort puls med mycket stor amplitud på den och se vad som händer vid utgången. Tja, det är inte klart vad som finns inuti denna fyrpol, eftersom det inte är klart hur man ska beskriva det, men vi kommer åtminstone att se något.
Här måste sägas att en kort (allmänt sett, oändligt kort) puls med stor (allmänt sett, oändlig) amplitud i teorin kallas en deltafunktion. Förresten, det roliga är att integralen av detta ändlös funktion är lika med en. Detta är normaliseringen.
Så det vi såg vid utgången av fyrpolsnätverket, efter att ha applicerat deltafunktionen på ingången, kallas impulsivt svar denna fyrpol. För nu är det dock inte klart hur det kommer att hjälpa oss, men låt oss bara komma ihåg resultatet och gå vidare till nästa intressanta koncept.
2. Konvolution.
Kort sagt, faltning är en matematisk operation som handlar om att integrera produkten av funktioner:
Som du kan se indikeras det med en asterisk. Du kan också se att under faltning tas en funktion i sin "framåtgående" ordning, och vi går igenom den andra "bakåt till fronten". Naturligtvis, i det diskreta fallet, som är mer värdefullt för mänskligheten, går faltningen, som vilken integral som helst, till summering:
Det skulle verka som någon form av tråkig matematisk abstraktion. Men i själva verket är en bunt kanske det mest magiska fenomenet i den här världen, näst efter födelsen av en person, näst efter födelsen av en person, med den enda skillnaden att de flesta får reda på var barn kommer ifrån åtminstone vid en ålder av arton, medan om vad en veckling är och varför den är användbar och fantastisk, har en stor del av jordens befolkning absolut ingen aning om hela sitt liv.
Så, kraften i denna operation ligger i det faktum att om f är någon godtycklig insignal och g är impulssvaret för ett nätverk med fyra portar, så kommer resultatet av faltningen av dessa två funktioner att likna det vi skulle få genom att skicka signalen f genom detta nätverk med fyra portar.
Det vill säga, impulssvaret är en komplett cast av alla egenskaper hos fyrportsnätverket i förhållande till ingångseffekten, och faltning av insignalen med den gör att du kan återställa motsvarande utsignal. Enligt mig är detta helt enkelt fantastiskt!
3. Filter.
Du kan göra många intressanta saker med impulsrespons och konvolution. Till exempel, om signalen är ljud, kan du organisera efterklang, eko, refräng, flanger och mycket, mycket mer; du kan differentiera och integrera... Generellt sett kan du skapa vad som helst. För oss nu är det viktigaste att naturligtvis även filter enkelt kan erhållas med hjälp av faltning.
Det digitala filtret i sig är faltningen av insignalen med ett impulssvar som motsvarar det önskade filtret.
Men självklart måste impulssvaret erhållas på något sätt. Vi har naturligtvis redan räknat ut hur man mäter det ovan, men i en sådan uppgift är det liten mening med detta - om vi redan har monterat filtret, varför mäta något annat, vi kan använda det som det är. Och dessutom är det viktigaste värdet av digitala filter att de kan ha egenskaper som är ouppnåeliga (eller mycket svåra att uppnå) i verkligheten - till exempel linjär fas. Så det finns inget sätt att mäta här alls, det är bara att räkna.
4. Få impulssvar.
Vid denna tidpunkt, i de flesta publikationer om ämnet, börjar författarna dumpa berg av Z-transformationer och fraktioner från polynom på läsaren, vilket gör honom fullständigt förvirrad. Jag kommer inte att göra det här, jag ska bara kort förklara vad allt detta handlar om och varför det i praktiken inte är särskilt nödvändigt för den progressiva allmänheten.
Låt oss säga att vi har bestämt vad vi vill ha från ett filter och skapat en ekvation som beskriver det. Därefter, för att hitta impulssvaret, kan du ersätta deltafunktionen i den härledda ekvationen och få den önskade. Det enda problemet är hur man gör detta, eftersom deltafunktionen är i tid O regionen ges av ett listigt system, och i allmänhet finns det alla möjliga oändligheter. Så i det här skedet visar allt sig vara fruktansvärt svårt.
Det är här det händer att de kommer ihåg att det finns något sådant som Laplace-transformen. I sig är det inte ett halvt kilo russin. Det enda skälet till att det tolereras inom radioteknik är just det faktum att inom ramen för det argument som denna transformation är en övergång till, blir vissa saker faktiskt enklare. I synnerhet samma deltafunktion som gav oss så mycket problem i tidsdomänen är väldigt lätt att uttrycka - där är det bara en!
Z-transformen (alias Laurent-transformen) är en version av Laplace-transformen för diskreta system.
Det vill säga, genom att applicera Laplace-transformen (eller Z-transformen, efter behov) på funktionen som beskriver det önskade filtret, ersätta ett till det resulterande och transformera tillbaka, får vi impulssvaret. Det låter enkelt, vem som helst kan prova det. Jag kommer inte att riskera det, för som redan nämnts är Laplace-transformen en hård sak, särskilt den omvända. Låt oss lämna det som en sista utväg, och vi kommer att leta efter några enklare sätt att få det vi letar efter. Det finns flera av dem.
För det första kan vi komma ihåg ett annat fantastiskt faktum i naturen - amplitudfrekvensen och impulsegenskaperna är relaterade till varandra genom den goda och välbekanta Fouriertransformen. Detta innebär att vi kan rita vilket frekvenssvar som helst efter vår smak, ta den inversa Fouriertransformen från den (antingen kontinuerlig eller diskret) och få impulssvaret från systemet som implementerar den. Det här är helt enkelt fantastiskt!
Detta kommer dock inte att vara problemfritt. För det första kommer impulssvaret vi får med största sannolikhet att vara oändligt (jag kommer inte att gå in på förklaringar till varför, det är så världen fungerar), så vi måste ta ett frivilligt beslut att avbryta det någon gång (inställning det är lika med noll bortom den punkten). Men detta kommer inte att hända bara som det - konsekvensen av detta, som man kan förvänta sig, kommer att vara förvrängning av frekvenssvaret för det beräknade filtret - det kommer att bli vågigt, och frekvensgränsen kommer att bli suddig.
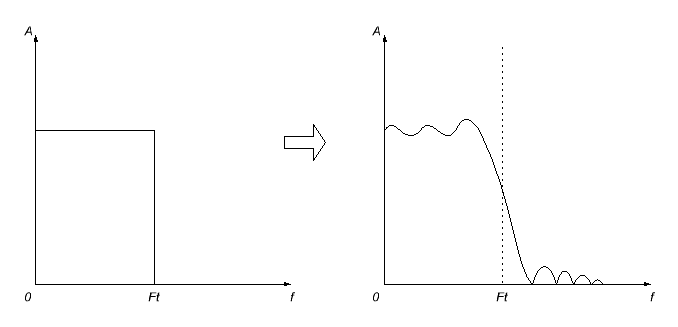
För att minimera dessa effekter tillämpas olika utjämningsfönsterfunktioner på det förkortade impulssvaret. Som ett resultat blir frekvenssvaret vanligtvis suddigt ännu mer, men obehagliga (särskilt i passbandet) svängningar försvinner. 
Efter en sådan bearbetning får vi faktiskt ett arbetsimpulssvar och kan bygga ett digitalt filter.
Den andra beräkningsmetoden är ännu enklare - impulssvaren från de mest populära filtren har länge uttryckts i analytisk form för oss. Allt som återstår är att ersätta dina värden och tillämpa fönsterfunktionen på resultatet efter eget tycke. Så du behöver inte ens överväga några transformationer.
Och, naturligtvis, om målet är att efterlikna beteendet hos en specifik krets, kan du få dess impulssvar i simulatorn:
Här applicerade jag en puls på 100500 volt (ja, 100,5 kV) med en varaktighet på 1 μs till ingången på RC-kretsen och fick dess impulssvar. Det är klart att detta inte kan göras i verkligheten, men i simulatorn fungerar denna metod, som du kan se, utmärkt.
5. Anteckningar.
Det som ovan sagts om att förkorta impulssvaret gällde givetvis det sk. ändliga impulssvarsfilter (FIR/FIR-filter). De har ett gäng värdefulla egenskaper, inklusive linjär fas (under vissa förhållanden för att konstruera impulssvaret), vilket säkerställer frånvaron av signalförvrängning under filtrering, såväl som absolut stabilitet. Det finns också oändliga impulssvarsfilter (IIR/IIR-filter). De är mindre resurskrävande beräkningsmässigt, men har inte längre de angivna fördelarna.
I nästa artikel hoppas jag kunna titta på ett enkelt exempel på den praktiska implementeringen av ett digitalt filter.
NOVOSIBIRSK STATENS TEKNISKA UNIVERSITET
FAKULTETET FÖR AUTOMATION OCH DATATEKNIK
Institutionen för datainsamlings- och bearbetningssystem
Disciplin "Teori och signalbehandling"
LABORATORIEARBETE NR.10
DIGITALA FILTER
MED FINIT IMPULS KARAKTERISTIK
Grupp: AT-33
Alternativ: 1 Lärare:
Studerande: Shadrina A.V. Assoc. Shchetinin Yu.I.
Målet med arbetet: studie av metoder för analys och syntes av finita impulssvarsfilter med hjälp av utjämningsfönsterfunktioner.
Slutförande av arbetet:
1. Impulssvarsdiagram av ett lågpass FIR-filter med en rektangulär fönstergränsfrekvens för värden på filterlängd och .
Impulssvaret för ett idealiskt diskret FIR-filter har oändlig längd och är inte noll för negativa värden på:
.
För att erhålla ett fysiskt genomförbart filter bör man begränsa impulssvaret till ett ändligt tal, och sedan flytta det trunkerade svaret åt höger med ett belopp.
Värdet är längden (storleken) på filtret, 
– filterordning.
Matlab Script (labrab101.m)
N = input("Ange filterlängd N = ");
h = sin(wc.*(n-(N-1)/2))./(pi.*(n-(N-1)/2));
xlabel("Referensnummer, n")
>> subplot(2,1,1)
>> labrab101
Ange filterlängden N = 15
>> title("Impulssvar av FIR-filter för N=15")
>> subplot(2,1,2)
>> labrab101
Ange filterlängd N = 50
>> title("Impulssvar av FIR-filter för N=50")
Figur 1. Impulssvarsdiagram av ett lågpass FIR-filter med en rektangulär fönstergränsfrekvens för värden på filterlängd och
En kommentar: Om vi betraktar frekvenssvaret för ett digitalt filter som en Fourier-serie: 
, då kommer koefficienterna för denna serie att representera värdena för filtrets impulssvar. I det här fallet trunkerades Fourier-serien i det första fallet till , och i det andra - till , och sedan flyttades de trunkerade egenskaperna längs provaxeln åt höger för att erhålla ett kausalt filter. När huvudlobens bredd är 2, och när - 1, dvs. När filterlängden ökar, smalnar impulssvarets huvudlob. Om vi tar hänsyn till nivån på sidoloberna (med hjälp av ), så ökar den i absolut värde från till . Således kan vi dra slutsatsen att när man använder en approximation av det ideala frekvenssvaret för ett filter med ett rektangulärt fönster, är det omöjligt att samtidigt minska huvudloben (och därigenom minska övergångsregionen) och minska nivåerna på sidoloberna (minska rippel i filtrets passband och stoppband). Den enda kontrollerbara parametern för ett rektangulärt fönster är dess storlek, med vilken du kan påverka bredden på huvudloben, men det har inte mycket effekt på sidoloberna.
2. Beräkning av DVFT för impulsegenskaperna från steg 1 med hjälp av funktionen. Grafer över deras frekvenssvar på linjär skala och i decibel för 512 frekvensprover. Filtrets passband, övergångsband och stoppband. Filterordningens inverkan på övergångsbandets bredd och nivån av frekvenssvarsrippel i pass- och stoppbanden.
Matlab-funktion (DTFT.m)
funktion = DTFT(x,M)
N = max(M, längd(x));
% Reducerar FFT till storlek 2^m
N = 2^(tak(log(N)/log(2)));
% Beräkna fft
% Frekvensvektor
w = 2*pi*((0:(N-1))/N);
w = w - 2*pi*(w>=pi);
% Skift FFT för att variera från -pi till +pi
X = fftshift(X);
w = fftshift(w);
Matlab Script (labrab102.m)
hl = sin(wc.*(nl-(N1-1)/2))./(pi.*(nl-(N1-1)/2));
h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));
DTFT(h1,512);
DTFT(h2,512);
plot(w./(2*pi),abs(H1)./max(abs(H1)),,"r")
xlabel("f, Hz"), ylabel("|H1|/max(|H1|)"), rutnät
plot(w./(2*pi),abs(H2)./max(abs(H2)),,"b")
xlabel("f, Hz"), ylabel("|H2|/max(|H2|)"), rutnät
plot(w./(2*pi),20*log10(abs(H1)),,"r")
title("Frekvenssvar för ett lågpass FIR-filter med ett rektangulärt fönster för N = 15")
xlabel("f, Hz"), ylabel("20lg(|H1|), dB"), rutnät
plot(w./(2*pi),20*log10(abs(H2)),"b")
title("Frekvenssvar för ett lågpass FIR-filter med ett rektangulärt fönster för N = 50")
xlabel("f, Hz"), ylabel("20lg(|H2|), dB"), rutnät
Fig.2. Frekvenssvarsdiagram av ett lågpass FIR-filter med en rektangulär fönstergränsfrekvens för filterlängdvärden och på en linjär skala
Fig.3. Frekvenssvarsdiagram för ett lågpass FIR-filter med en rektangulär fönstergränsfrekvens för filterlängdvärden och på en logaritmisk skala
En kommentar:
Bord 1. Omfång för passband, övergångsområde och stoppband för filterlängd och
|
Filterlängd |
Bandbredd, Hz |
Övergångsområde, Hz |
Stoppband, Hz |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Föreläsning nr 10 "Digitala filter med ändlig impulsrespons" Överföringsfunktionen för ett fysiskt realiserbart digitalt finita impulssvarsfilter (FIR-filter) kan representeras som (10.1). När vi ersätter i uttryck (10.1) får vi FIR-filtrets frekvenssvar i formen Var Fasfördröjning filter definieras som Gruppfördröjning filter definieras som En utmärkande egenskap hos FIR-filter är möjligheten att implementera konstanta fas- och gruppfördröjningar, d.v.s. linjär fasrespons (10.5), där en - konstant. Om detta villkor är uppfyllt, förvränger inte signalen som passerar genom filtret dess form. För att härleda villkoren som säkerställer ett linjärt fassvar, skriver vi FIR-filtrets frekvenssvar med hänsyn till (10.5) Genom att likställa de verkliga och imaginära delarna av denna jämlikhet får vi Om vi dividerar den andra ekvationen med den första får vi Äntligen kan vi skriva Denna ekvation har två lösningar. Först när a =0 motsvarar ekvationen Denna ekvation har en unik lösning som motsvarar en godtycklig h (0) (sin (0)=0), och h (n)=0 för n >0. Denna lösning motsvarar ett filter vars impulssvar har ett enda prov som inte är noll vid den initiala tiden. Ett sådant filter är inte av praktiskt intresse. Vi kommer att hitta en annan lösning för . I det här fallet får vi genom att korsmultiplicera täljarna och nämnare i (10.8) (10.11). Härifrån har vi Eftersom denna ekvation har formen av en Fourier-serie är dess lösning, om den finns, unik. Det är lätt att se att lösningen på denna ekvation måste uppfylla villkoren (10.13), (10.14). Av villkor (10.13) följer det för varje filterorder N det finns bara en fasfördröjning a , vid vilken strikt linjäritet för fassvaret kan uppnås. Av villkor (10.14) följer att filtrets impulssvar måste vara symmetriskt kring punkten för udda N , och i förhållande till intervallets mittpunkt (Fig. 10.1).
Frekvenssvaret för ett sådant filter (för udda N ) kan skrivas i formen (10.15). Göra en substitution i det andra beloppet m = N -1- n , vi får (10.16). Eftersom h (n)= h (N -1- n ), då kan de två beloppen kombineras Vi får ersätta (10.18). Om vi utser så kan vi äntligen skriva För ett filter med linjär fasrespons har vi alltså För fallet med jämnt N på samma sätt kommer vi att ha Att göra ett byte i den andra summan får vi Att göra bytet får vi (10.24). Efter att ha utsett vi kommer äntligen att ha Alltså för ett FIR-filter med linjär fasrespons och jämn ordning N kan skrivas I det följande kommer vi för enkelhets skull endast att överväga filter med en udda ordning. Vid syntetisering av filteröverföringsfunktionen är de initiala parametrarna som regel kraven på frekvensgången. Det finns många tekniker för att syntetisera FIR-filter. Låt oss titta på några av dem. Eftersom frekvenssvaret för alla digitala filter är en periodisk funktion av frekvensen, kan det representeras som en Fourier-serie där koefficienterna för Fourierserien är lika Det kan ses att koefficienterna för Fourier-serien h(n ) sammanfaller med filtrets impulssvarskoefficienter. Därför, om den analytiska beskrivningen av det erforderliga frekvenssvaret för filtret är känd, är det möjligt att enkelt bestämma koefficienterna för impulssvaret och från dem filtrets överföringsfunktion. I praktiken är detta emellertid inte genomförbart, eftersom impulssvaret för ett sådant filter har en oändlig längd. Dessutom är ett sådant filter inte fysiskt realiserbart eftersom impulssvaret börjar kl.¥ , och ingen ändlig fördröjning kommer att göra detta filter fysiskt realiserbart. En möjlig metod för att erhålla ett FIR-filter som approximerar ett givet frekvenssvar är att trunkera den oändliga Fourier-serien och impulssvaret för filtret, förutsatt att h (n)=0 vid . Sedan Fysisk realiserbarhet av överföringsfunktionen H(z ) kan uppnås genom att multiplicera H(z) på . Var (10.32). Med en sådan modifiering av överföringsfunktionen ändras inte amplitudkarakteristiken för filtret, och gruppfördröjningen ökar med ett konstant belopp. Som ett exempel, låt oss beräkna ett lågpass FIR-filter med ett frekvenssvar av formen I enlighet med (10.29) beskrivs av uttrycket Nu från (10.31) kan vi få ett uttryck för överföringsfunktionen Var (10.36). Amplitudegenskaper hos det beräknade filtret för olika N visas i fig. 10.2.
Fig.10.2 Rippling i passbandet och stoppbandet uppstår på grund av Fourier-seriens långsamma konvergens, vilket i sin tur orsakas av närvaron av en diskontinuitet i funktionen vid passbandets gränsfrekvens. Dessa pulsationer är kända som Gibbs krusning. Av fig. 10.2 framgår att med ökande N pulsationsfrekvensen ökar och amplituden minskar vid både lägre och högre frekvenser. Emellertid förblir amplituden för den sista rippeln i passbandet och den första rippeln i stoppbandet praktiskt taget oförändrad. I praktiken är sådana effekter ofta oönskade, vilket kräver att man hittar sätt att minska Gibbs pulsationer. Trunkerat impulssvar h(n ) kan representeras som produkten av det nödvändiga oändliga impulssvaret och några fönsterfunktioner w (n) av längden n (fig. 10.3).
I det övervägda fallet med enkel trunkering av Fourier-serien använder vi rektangulärt fönster I detta fall kan filtrets frekvenssvar representeras som en komplex faltning Detta innebär att det blir en "suddig" version av den nödvändiga egenskapen. Problemet handlar om att hitta fönsterfunktioner som gör det möjligt att minska Gibbs rippel med samma filterselektivitet. För att göra detta måste du först studera egenskaperna för fönsterfunktionen med hjälp av exemplet med ett rektangulärt fönster. Spektrum för den rektangulära fönsterfunktionen kan skrivas som Spektrum för den rektangulära fönsterfunktionen visas i fig. 10.4.
Fig.10.4 Sedan vid , visar sig bredden på spektrumets huvudlob vara lika med . Närvaron av sidolober i spektrumet av fönsterfunktionen leder till en ökning av Gibbs rippel i filtrets frekvenssvar. För att erhålla låg rippel i passbandet och hög dämpning i stoppbandet är det nödvändigt att arean som begränsas av sidoloberna är en liten del av den area som begränsas av huvudloben. I sin tur bestämmer bredden på huvudloben bredden på övergångszonen för det resulterande filtret. För hög filterselektivitet bör huvudlobens bredd vara så liten som möjligt. Som framgår av ovanstående minskar huvudlobens bredd med ökande filterordning. Således kan egenskaperna hos lämpliga fönsterfunktioner formuleras enligt följande: - fönsterfunktionen måste vara tidsbegränsad; - spektrumet för fönsterfunktionen bör bäst approximera den frekvensbegränsade funktionen, dvs. ha ett minimum av energi utanför huvudloben; - Bredden på huvudloben av fönsterfunktionsspektrumet bör vara så liten som möjligt. De vanligaste fönsterfunktionerna är: 1. Rektangulärt fönster. Diskuterat ovan. 2. Hammarfönster. Var . Detta fönster kallas Hann-fönstret ( hanning). 3. Blackman-fönster. 4. Bartletts fönster. Indikatorerna för filter byggda med de angivna fönsterfunktionerna sammanfattas i Tabell 10.1.
Rippelfaktorn definieras som förhållandet mellan sidolobens maximala amplitud och huvudlobens amplitud i fönsterfunktionens spektrum. För att välja önskad filterordning och den lämpligaste fönsterfunktionen vid beräkning av verkliga filter kan du använda data i Tabell 10.2.
Som framgår av Tabell 10.1 finns det ett visst samband mellan rippelkoefficienten och huvudlobens bredd i fönsterfunktionens spektrum. Ju mindre pulsationskoefficienten är, desto större är huvudlobens bredd och därför övergångszonen i filtrets frekvenssvar. För att säkerställa låg rippel i passbandet är det nödvändigt att välja ett fönster med en lämplig rippelkoefficient och tillhandahålla den erforderliga bredden på övergångszonen med en ökad filterordning N. Detta problem kan lösas med hjälp av fönstret som föreslagits av Kaiser. Kaiser-fönsterfunktionen har formen
där a är en oberoende parameter,
En attraktiv egenskap hos Kaiser-fönstret är möjligheten att smidigt ändra pulsationskoefficienten från små till stora värden, samtidigt som man bara ändrar en parameter a. I det här fallet, liksom för andra fönsterfunktioner, kan huvudlobens bredd justeras med filterordningen N. De viktigaste parametrarna som ställs in när man utvecklar ett riktigt filter är: Bandbredd - w p; Hinderremsa - w a ; Den maximalt tillåtna rippeln i passbandet är Ap; Minsta stoppbandsdämpning – A a ; -samplingsfrekvens - ws. Dessa parametrar illustreras i Fig. 10.5. I detta fall bestäms den maximala rippeln i passbandet som
och den minsta dämpningen i stoppbandet är som Den relativt enkla proceduren för att beräkna ett filter med ett Kaiser-fönster inkluderar följande steg: 1. Impulssvaret för filtret h (n) bestäms, förutsatt att frekvenssvaret är idealiskt
där (10.49). 2. Parameter d väljs som
Var 3. Det sanna värdet av A a och Ap beräknas med formler (10.46), (10.47). 4.Parameter a väljs som
5.Parameter D väljs som
6. Välj det minsta udda värdet i filterordningen från villkoret
följer det Eftersom samplen av filtrets impulssvar är koefficienterna för dess överföringsfunktion, betyder villkor (10.59) att koderna för alla filterkoefficienter endast innehåller bråkdelen och teckenbiten och inte innehåller heltalsdelen. Antalet siffror i bråkdelen av filterkoefficienterna bestäms från villkoret för att uppfylla filteröverföringsfunktionen med kvantiserade koefficienter, de specificerade kraven för att närma sig referensöverföringsfunktionen med exakta värden på koefficienterna. De absoluta värdena för filteringångssignalsamplen normaliseras vanligtvis så att Om analysen utförs för ett FIR-filter med ett linjärt fassvar, kan algoritmen för att beräkna dess utsignal vara som följer var är filterkoefficienterna avrundade till s k. Denna algoritm motsvarar filterblockdiagrammet som visas i fig. 10.5.
Det finns två sätt att implementera denna algoritm. I det första fallet utförs alla multiplikationsoperationer exakt och det finns ingen avrundning av produkter. I detta fall är bitdjupet för produkterna lika med s i +s k, där s in är bitdjupet för insignalen och sk är bitdjupet för filterkoefficienterna. I detta fall motsvarar blockschemat för filtret som visas i fig. 10.5 exakt det verkliga filtret. I den andra metoden för att implementera algoritmen (10.61) avrundas varje resultat av multiplikationsoperationen, dvs. produkter är beräknade med något fel. I det här fallet är det nödvändigt att ändra algoritmen (10.61) för att ta hänsyn till felet som introduceras genom att avrunda produkterna Om sampelvärdena för filterutgångssignalen beräknas med den första metoden (med exakta värden för produkterna), så bestäms spridningen av utgående brus som
de där. beror på variansen av avrundningsbruset för insignalen och värdena på filterkoefficienterna. Härifrån kan du hitta det erforderliga antalet bitar av insignalen som
Med hjälp av de kända värdena för s in och sk kan man bestämma antalet bitar som krävs för den del av utsignalkoden som Om värdena för utsignalsamplen beräknas med den andra metoden, när varje produkt avrundas till s d siffror, kan spridningen av avrundningsbruset som skapas av var och en av multiplikatorerna uttryckas i termer av sifferkapaciteten hos produkt som DR in och signal-brusförhållande vid filterutgången SNR ut. Det dynamiska området för insignalen i decibel definieras som
där A max och A min är maximi- och miniamplituderna för filteringångssignalen. Signal-brusförhållandet vid filterutgången, uttryckt i decibel, definieras som
bestämmer rotmedelvärdet för effekten av den sinusformade utsignalen från filtret med amplitud A min, och (10.77) bestämmer bruseffekten vid filterutgången. Från (10.75) och (10.76) med A max =1 får vi ett uttryck för spridningen av filterutgångsbruset Detta filterutgångsbrusspridningsvärde kan användas för att beräkna bitdjupet för filtrets in- och utsignaler.  En värld av gratis program och användbara tips 2024 whatsappss.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(10.2),
- amplitud-frekvenssvar (AFC) filtrera,
- fasfrekvenssvar (PFC) filtrera.
(10.3).
(10.4).
(10.6).
(10.7).
(10.8).
(10.9).
(10.10).
(10.12).
(10.17).
(10.19),
(10.20).
(10.21).
(10.22).
(10.23).
(10.25),
(10.26).
(10.27).
(10.28),
(10.29).
(10.30).
(10.31),
(10.33).
(10.34).
(10.35),
(10.37).
(10.38).
(10.39).
(10.40).
(10.41),
(10.42).
(10.43).
(10.44),
, I 0 – Besselfunktion av den första sortens nollordning, definierad av uttrycket
(10.45).
(10.46),
(10.50),
(10.51).
(10.52).
(10.53).
(10.54),
(10.57)
(10.66),
(10.67).
(10.74),
(10.75),
(10.78).