Impulzní odezva filtru. Digitální filtry s konečnou impulsní odezvou. Vyhlazování dat. Mediánové filtrování
48 Digitální filtry s konečnou impulsní odezvou. Výpočet kih filtrů.
Filtr konečných impulsů (Nerekurzivní filtr, FIR filtr) nebo FIR filtr (FIR je zkratka z finite impulse response - finite impulse response) - jeden z typů lineárních číslicových filtrů, jehož charakteristickým rysem je jeho časové omezení impulsní odezva(od určitého okamžiku se přesně rovná nule). Takový filtr se také nazývá nerekurzivní kvůli nedostatku zpětné vazby. Jmenovatelem přenosové funkce takového filtru je určitá konstanta.
Diferenční rovnice popisující vztah mezi vstupními a výstupními signály filtru: kde P- pořadí filtrů, X(n) - vstupní signál, y(n) je výstupní signál a b i- filtrační koeficienty. Jinými slovy, hodnota libovolného vzorku výstupního signálu je určena součtem škálovaných hodnot P předchozí čtení. Dá se to říci jinak: hodnota výstupu filtru v každém okamžiku je hodnota odezvy na okamžitou hodnotu vstupu a součet všech postupně se snižujících odezev P předchozí vzorky signálu, které stále ovlivňují výstup (po P-počítá, pulzní přechodová funkce se rovná nule, jak již bylo zmíněno, proto všechny členy za P-th bude také roven nule). Napišme předchozí rovnici v prostornějším tvaru:
Abychom našli jádro filtru, vložili jsme
X(n) = δ( n)
kde δ( n) - funkce delta. Potom lze impulsní odezvu FIR filtru zapsat jako:
Z-transformace impulsní odezvy nám dává přenosovou funkci FIR filtru:
]Vlastnosti
FIR filtr má řadu užitečných vlastností, díky kterým je někdy vhodnější jej použít než IIR filtr. Tady jsou některé z nich:
FIR filtry jsou robustní.
FIR filtry při implementaci nevyžadují zpětnou vazbu.
Fáze FIR filtrů může být lineární
Přímá forma FIR filtru
Filtry FIR lze implementovat pomocí tří prvků: násobiče, sčítačky a bloku zpoždění. Možnost zobrazená na obrázku je přímou implementací FIR filtrů typu 1.
Implementace přímé formy FIR filtru
Příklad programu
Níže je příklad programu FIR filtr napsaný v C:
/* FIR filtr pro 128 kohoutků */
float fir_filter (float input)
statický plovoucí vzorek;
acc = 0,0f; /* baterie */
/* Násobit a hromadit */
pro (i = 0; i< 128; i++) {
acc += (h[i] * vzorek[i]);
/* Konec */
/* Posunout zpožděný signál */
pro (i = 127; i > 0; i--)
vzorek[i] = vzorek;
49 Vyhlazování dat. Pohyblivé průměrování.
50 Vyhlazování dat. Parabolické vyhlazení.
51 Vyhlazování dat. Spencer vyhlazení.
52 Vyhlazování dat. Mediánové filtrování.
Pohyblivé průměrování, parabolické vyhlazování, Spencerovo vyhlazování, střední filtrování
Při vývoji metod pro určování parametrů fyzikálních procesů, které se pomalu mění v čase, je důležitým úkolem eliminovat vliv šumových efektů nebo náhodné interference, které se superponují na zpracovávaný signál přijímaný na výstupu primárního převodníku.
Chcete-li tento efekt eliminovat, můžete použít vyhlazování dat. Jednou z nejjednodušších metod takového vyhlazování je aritmetický průměr. Při jeho použití se každá hodnota diskrétní funkce (pole zpracovaných dat) vypočítá v souladu s výrazem:
kde je počet bodů pro aritmetické průměrování (liché celé číslo);
Hodnota funkce před zpracováním;
Existují i jiné docela účinné metody vyhlazování, například s parabolami druhého stupně v pěti, sedmi, devíti a jedenácti bodech v souladu s výrazy:
nebo paraboly čtvrtého stupně v sedmi, devíti, jedenácti a třinácti bodech:
V praktických aplikacích poskytují dobré výsledky jiné účinné metody, například 15bodové Spencerovo vyhlazování:
Dosazením komplexní exponenciály , kde do těchto výrazů můžeme určit přenosovou funkci příslušné transformace.
Pro aritmetické průměrování
Výraz v závorkách představuje geometrickou posloupnost se jmenovatelem, proto může být tento výraz reprezentován jako:
.
Tento vzorec představuje přenosovou charakteristiku dolnopropustného filtru a ukazuje, že čím více členů se účastní průměrování, tím větší je potlačení složek vysokofrekvenčního šumu v signálu (viz obrázek 6.1).
Sémantický koncept frekvence při zpracování časových trendů se však liší od podobného pojetí při zpracování signálů. To se vysvětluje tím, že při studiu časových trendů není zajímavé jejich frekvenční složení, ale typ změny (nárůst, pokles, stálost, cykličnost atd.).
Použití tzv. heuristických algoritmů je také docela efektivní pro vyhlazování dat.
Jedním z nich je střední filtrování. Při jeho implementaci v klouzavém časovém okně dimenze , kde je celé číslo liché, je centrální prvek nahrazen prostředním prvkem sekvence, což jsou ve vzestupném pořadí hodnot prvky datového pole vyhlazeného signál spadající do časového okna. Výhodou střední filtrace je schopnost odstranit impulsní šum, jehož trvání nepřesahuje, prakticky bez zkreslení plynule se měnících signálů. Tato metoda potlačení hluku nemá striktní matematické opodstatnění, ale jednoduchost výpočtů a efektivita získaných výsledků vedly k jejímu širokému použití.
Obrázek 6.1 - Grafy přenosových charakteristik
aritmetické operace průměrování pro m=5, 7, 9, 11
Dalším zajímavým vyhlazovacím algoritmem je střední průměrování. Jeho podstata je následující. V posuvném časovém okně velikosti (-liché celé číslo) jsou prvky datového pole seřazeny ve vzestupném pořadí a poté jsou z uspořádané sekvence odstraněny první a poslední prvky (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
Tato metoda umožňuje potlačit pulsní a vysokofrekvenční rušení a také dosáhnout dobrého vyhlazení signálu.
| " |
Vezměme si nejjednodušší z digitálních filtrů - filtry s konstantními parametry.
Vstupní signál digitálního filtru je dodáván ve formě sekvence číselných hodnot, které následují v intervalech (obr. 4.1, a). Když je v digitálním filtru přijata každá další hodnota signálu, je vypočítána další hodnota výstupního signálu.Výpočtové algoritmy mohou být velmi rozmanité; během procesu výpočtu lze kromě poslední hodnoty vstupního signálu použít
předchozí hodnoty vstupních a výstupních signálů: Výstupní signál digitálního filtru je také posloupnost číselných hodnot v intervalu . Tento interval je stejný pro celé zařízení pro digitální zpracování signálu.
Rýže. 4.1. Signál na vstupu a výstupu digitálního filtru
Pokud tedy přivedete nejjednodušší signál ve formě jediného impulsu na vstup digitálního filtru (obr. 4.2, a)
pak na výstupu dostaneme signál ve formě diskrétní sekvence číselných hodnot, které následují v intervalech
Analogicky s konvenčními analogovými obvody budeme tento signál odpovědi nazývat impulsní odezva filtru (obr. 4.2, b). Na rozdíl od impulsní odezvy analogového obvodu je funkce bezrozměrná.
Rýže. 4.2. Jednotkový impuls a impulsní odezva digitálního filtru
Aplikujme na vstup filtru libovolný diskrétní signál (obr. 4.1, a), což je soubor diskrétních hodnot
Při působení prvního prvku se na výstupu filtru vytvoří sekvence vynásobená hodnotou, při akci se sekvence vynásobí a posune doprava o hodnotu atd. Výsledkem je, že výstup získá sekvence kde
Výstupní signál je tedy definován jako diskrétní konvoluce vstupního signálu a impulsní odezvy. V tomto ohledu jsou digitální filtry podobné konvenčním obvodům, kde se výstupní signál rovná konvoluci vstupního signálu a impulsní odezvě.
Vzorec (4.1) je algoritmus digitálního filtrování. Pokud je impulsní odezva filtru popsána sekvencí s konečným počtem členů, pak lze filtr implementovat ve formě obvodu znázorněného na Obr. 4.3. Zde písmeno označuje prvky zpoždění signálu pro čas (na buňku); -prvky, které násobí signál odpovídajícím koeficientem.
Schéma znázorněné na Obr. 4.3 není elektrický obvod digitálního filtru; Tento diagram je grafickým znázorněním algoritmu digitálního filtrování a ukazuje sekvenci aritmetických operací prováděných během zpracování signálu.
Rýže. 4.3. Nerekurzivní digitální filtrační obvod
Pro digitální filtry, které zpracovávají signály ve formě abstraktních číselných sekvencí, není pojem „časové zpoždění“ zcela správný. Proto jsou prvky, které zpožďují signál o jednu buňku, na obvodech číslicových filtrů obvykle označeny symbolem označujícím zpoždění signálu v jazyce -transformací. V následujícím textu se budeme tohoto označení držet.
Vraťme se k digitálnímu filtračnímu obvodu znázorněnému na Obr. 4.3, Takové filtry, kde se pro výpočet používají pouze hodnoty vstupního signálu, se nazývají jednoduché nebo nerekurzivní.
Algoritmus nerekurzivního filtru lze snadno napsat, pokud je známa impulsní odezva filtru. Pro praktickou implementaci algoritmu je nutné, aby impulsní odezva obsahovala konečný počet členů. Pokud impulsní odezva obsahuje nekonečný počet termínů, ale jejich hodnota rychle klesá, můžete se omezit na konečný počet termínů a vyřadit ty, jejichž hodnoty jsou malé. Pokud se hodnota prvků impulsní odezvy nesníží, algoritmus nerekurzivního filtru se ukáže jako nerealizovatelný.
Rýže. 4.4. -řetěz
Jako příklad uvažujme nejjednodušší digitální filtr, podobný -obvodu (obr. 4.4). Impulzní odezva obvodu má tvar
K zápisu impulsní odezvy odpovídajícího digitálního filtru by měl být výraz nahrazen výrazem Impulsní odezva obvodu má však rozměr a impulsní odezva digitálního filtru musí být bezrozměrná. Ve výrazu (4.2) proto vynecháme násobitel a impulsní odezvu digitálního filtru zapíšeme ve tvaru
Taková impulsní odezva obsahuje nekonečně mnoho členů, ale jejich velikost se zmenšuje podle exponenciálního zákona a my se můžeme omezit na členy a vybrat takové,
Nyní můžeme napsat výraz pro signál na výstupu filtru
Tento výraz je také algoritmem digitálního filtru. Schéma tohoto filtru je na Obr. 4.5.
Druhý přístup k analýze procesů v digitálních filtrech je podobný operátorské metodě analýzy konvenčních analogových obvodů, pouze místo Laplaceovy transformace je použita -transformace.
Rýže. 4.5. Obvod nerekurzivního digitálního filtru podobný -obvodu
Definujme parametr digitálního filtru podobný přenosové funkci elektrického obvodu. Chcete-li to provést, použijte transformaci na impulsní odezvu digitálního filtru:
Funkce se nazývá funkce filtru systému.
V souladu s výrazem (4.1) je signál na výstupu digitálního filtru roven diskrétní konvoluci vstupního signálu a impulsní odezvě filtru. Aplikováním konvoluční věty na tento výraz získáme, že transformace výstupního signálu je rovna transformaci vstupního signálu vynásobené funkcí systémového filtru:
Systémová funkce tedy hraje roli přenosové funkce digitálního filtru.
Jako příklad najdeme systémovou funkci digitálního filtru prvního řádu podobného obvodu:
Třetí metoda analýzy průchodu signálů digitálními filtry je podobná klasické metodě diferenciálních rovnic. Zvažme tuto metodu pomocí objednávkových řetězců jako příkladu.
Nejjednodušším analogovým obvodem 1. řádu je -obvod (viz obr. 4.4), průchod signálů, který popisuje diferenciální rovnice
Pro diskrétní obvod by se místo diferenciální rovnice (4.8) měla napsat diferenční rovnice, kde jsou vstupní a výstupní signály specifikovány pro diskrétní časové okamžiky a místo derivace by měl být zapsán rozdíl hodnot sousedních signálů. objevit. Pro diskrétní obvod 1. řádu lze diferenční rovnici zapsat v poměrně obecné podobě
Aplikujme transformaci na rovnici
kde najdeme funkci systémového filtru
Vzorec (4.10) je poměrně obecný výraz pro systémovou funkci digitálního filtru 1. řádu. Když se shoduje s dříve získaným výrazem (4.7) pro systémovou funkci digitálního filtru ekvivalentního -obvodu.
Najdeme algoritmus číslicové filtrace odpovídající systémové funkci (4.10). K tomu vyřešíme rovnici (4.9) pro
Ekvivalentní schéma tohoto algoritmu je znázorněno na obr. 4.6. Oproti nerekurzivnímu filtru (viz obr. 4.5) zde přibyl jakýsi „obvod zpětné vazby“, což znamená, že hodnoty výstupního signálu jsou použity v následných
Rýže. 4.6. Obvod rekurzivního digitálního filtru podobný -obvodu
výpočty. Filtry tohoto typu se nazývají rekurzivní.
Algoritmus (4.11) odpovídá filtru, který je zcela ekvivalentní nerekurzivnímu filtru zvažovanému dříve. Ale pro určení jedné hodnoty výstupního signálu pomocí algoritmu nerekurzivního filtru (4.4) je nutné provést operace a při použití algoritmu rekurzivního filtru (4.11) jsou potřeba pouze dvě operace. To je hlavní výhoda rekurzivních filtrů. Rekurzivní filtry navíc umožňují zpracování signálu s vyšší přesností, protože umožňují správnější implementaci impulsní odezvy bez vyřazení jejího „ocasu“. Rekurzivní filtry umožňují implementovat algoritmy, které nelze vůbec implementovat pomocí nerekurzivních filtrů. Například s filtrem pracujícím podle obvodu na Obr. 4.6, je v podstatě ideální akumulátor-integrátor a má impulsní odezvu tvaru Filtr s takovou charakteristikou nelze realizovat pomocí nerekurzivního schématu.
Uvažované příklady ukazují, že nemá smysl používat nerekurzivní algoritmy k vytváření digitálních filtrů s dlouhou impulsní odezvou. V těchto případech je vhodnější použít rekurzivní filtry.
Oblastí použití nerekurzivních algoritmů je implementace digitálních filtrů s impulsní odezvou obsahující malý počet členů. Příkladem je nejjednodušší diferenciátor, jehož výstupní signál se rovná přírůstku vstupního signálu:
Obvod takového digitálního filtru je znázorněn na Obr. 4.7.
Rýže. 4.7. Obvod nejjednoduššího digitálního derivátoru
Uvažujme nyní obecný digitální filtr, který je popsán rovnicí
Tuto rovnici lze považovat jak za diferenční rovnici řádu, tak za algoritmus digitálního filtrování, pokud je přepsána jinak, tj.
Rýže. 4.8. Rekurzivní obvod digitálního řádu
Algoritmus (4.13) odpovídá obvodu znázorněnému na Obr. 4.8. Pojďme najít systémovou funkci takového filtru. Chcete-li to provést, použijte transformaci na rovnici:
Výraz (4.14) nám umožňuje navázat spojení mezi kolísáním prvků filtračního obvodu a funkcí systému. Koeficienty v čitateli systémové funkce určují hodnoty koeficientů pro
(v nerekurzivní části filtru) a koeficienty ve jmenovateli určují rekurzivní část filtru.
Všechno to začalo, když přítel přítele přítele potřeboval pomoc s těmito stejnými filtry. Prostřednictvím způsobů Jedi se ke mně dostaly zvěsti o tom, odhlásil jsem se v komentářích k příspěvku na odkazu. Zdálo se, že to pomáhá. No, doufám.
Tento příběh ve mně rozdmýchal vzpomínky na třetí, nebo tak nějak, kurz, kdy jsem sám nastupoval do DSP, a podnítil mě k napsání článku pro všechny, které zajímá, jak fungují digitální filtry, ale přirozeně je děsí nad -vrcholové vzorce a psychedelické kresby v (to už nemluvím o učebnicích).
Obecně podle mých zkušeností situaci s učebnicemi popisuje známá věta, že někdy pro stromy nevidíte les. A to znamená, že když vás okamžitě začnou děsit Z-transformací a vzorci pro dělení polynomů, které jsou často delší než dvě desky, zájem o téma extrémně rychle oschne. Začneme jednoduchým, naštěstí pro pochopení toho, co se děje, není vůbec nutné popisovat dlouhé složité výrazy.
Nejprve tedy několik jednoduchých základních pojmů.
1. Impulsní reakce.
Řekněme, že máme krabici se čtyřmi kolíky. Nemáme ponětí, co je uvnitř, ale víme jistě, že dva levé terminály jsou vchod a dva pravé jsou východ. Zkusme na něj aplikovat velmi krátký pulz s velmi velkou amplitudou a uvidíme, co se stane na výstupu. No, není jasné, co je uvnitř tohoto čtyřpólu, protože není jasné, jak to popsat, ale alespoň něco uvidíme.
Zde je třeba říci, že krátký (obecně řečeno nekonečně krátký) puls velké (obecně řečeno nekonečné) amplitudy se teoreticky nazývá delta funkce. Mimochodem, legrační je, že integrál tohoto nekonečný funkce je rovna jedné. To je ta normalizace.
Takže to, co jsme viděli na výstupu kvadripólové sítě, po aplikaci funkce delta na vstup, se nazývá impulsní odezva tento čtyřpól. Zatím však není jasné, jak nám to pomůže, ale připomeňme si získaný výsledek a přejděme k dalšímu zajímavému konceptu.
2. Konvoluce.
Stručně řečeno, konvoluce je matematická operace, která spočívá v integraci součinu funkcí:
Jak vidíte, je to označeno hvězdičkou. Můžete také vidět, že během konvoluce je jedna funkce převzata v pořadí „dopředu“ a druhou procházíme „zpět dopředu“. Samozřejmě, že v diskrétním případě, který je pro lidstvo cennější, konvoluce, jako každý integrál, jde do součtu:
Vypadalo by to jako nějaká tupá matematická abstrakce. Ve skutečnosti je však svazek snad nejkouzelnějším fenoménem tohoto světa, hned po narození člověka je druhý v úžasnosti, jen s tím rozdílem, že většina lidí zjistí, odkud děti pocházejí, minimálně ve věku let. osmnáct, zatímco o tom, co je konvoluce a proč je užitečná a úžasná, velká část populace Země nemá po celý život absolutně žádnou představu.
Síla této operace tedy spočívá ve skutečnosti, že pokud f je libovolný vstupní signál a g je impulsní odezva sítě se čtyřmi porty, pak výsledek konvoluce těchto dvou funkcí bude podobný tomu, jaký bychom měli získat průchodem signálu f touto čtyřportovou sítí.
To znamená, že impulsní odezva je úplným obsazením všech vlastností čtyřportové sítě ve vztahu ke vstupnímu efektu a konvoluce vstupního signálu s ní umožňuje obnovit odpovídající výstupní signál. Podle mého názoru je to prostě úžasné!
3. Filtry.
S impulsní odezvou a konvolucí můžete dělat spoustu zajímavých věcí. Například, pokud je signál audio, můžete uspořádat reverb, echo, chorus, flanger a mnohem, mnohem více; můžete rozlišovat a integrovat... Obecně lze vytvořit cokoliv. Pro nás je nyní nejdůležitější, že filtry lze samozřejmě snadno získat i pomocí konvoluce.
Vlastní digitální filtr je konvolucí vstupního signálu s impulsní odezvou odpovídající požadovanému filtru.
Ale samozřejmě, impulsní odezva se musí nějak získat. Samozřejmě jsme již přišli na to, jak to změřit výše, ale v takové úloze to má malý smysl - pokud jsme již filtr sestavili, proč měřit něco jiného, můžeme jej použít tak, jak je. A kromě toho nejdůležitější hodnotou digitálních filtrů je to, že mohou mít ve skutečnosti nedosažitelné (nebo velmi obtížně dosažitelné) vlastnosti – například lineární fázi. Zde se tedy vůbec nedá měřit, stačí jen počítat.
4. Získání impulsní odezvy.
V tuto chvíli začnou autoři ve většině publikací na toto téma na čtenáře vysypat hory Z-transformací a zlomků z polynomů, čímž ho zcela zmate. Nebudu to dělat, jen stručně vysvětlím, o čem to všechno je a proč to v praxi pro pokrokovou veřejnost není příliš nutné.
Řekněme, že jsme se rozhodli, co od filtru chceme, a vytvořili rovnici, která to popisuje. Dále, abyste našli impulsní odezvu, můžete do odvozené rovnice dosadit delta funkci a získat požadovanou. Jediný problém je, jak to udělat, protože funkce delta je v čase Ó oblast je dána mazaným systémem a obecně existují nejrůznější nekonečna. Takže v této fázi se vše ukazuje jako strašně těžké.
Tady se stává, že si vzpomenou, že existuje něco jako Laplaceova transformace. Samo o sobě to není půl kila rozinek. Jediným důvodem, proč je v radiotechnice tolerována, je právě skutečnost, že v prostoru argumentace, ke které je tato transformace přechodem, se některé věci skutečně zjednodušují. Zejména stejná delta funkce, která nám dělala tolik problémů v časové oblasti, je velmi snadno vyjádřena - tam je jen jedna!
Z-transformace (aka Laurentova transformace) je verze Laplaceovy transformace pro diskrétní systémy.
To znamená, že aplikací Laplaceovy transformace (nebo Z-transformace, podle potřeby) na funkci popisující požadovaný filtr, dosazením jednoho do výsledného filtru a zpětné transformace získáme impulsní odezvu. Zní to jednoduše, zkusit to může každý. Nebudu to riskovat, protože, jak již bylo zmíněno, Laplaceova transformace je krutá věc, zvláště ta obrácená. Nechme to jako poslední možnost a budeme hledat nějaké jednodušší způsoby, jak získat to, co hledáme. Je jich několik.
Nejprve si můžeme připomenout další úžasný přírodní fakt – amplitudově-frekvenční a impulsní charakteristiky jsou vzájemně propojeny dobrou a známou Fourierovou transformací. To znamená, že si můžeme nakreslit libovolnou frekvenční odezvu podle svého vkusu, vzít z ní inverzní Fourierovu transformaci (buď spojitou nebo diskrétní) a získat impulsní odezvu systému, který ji implementuje. To je prostě úžasné!
To se však neobejde bez problémů. Zaprvé, impulsní odezva, kterou dostaneme, bude s největší pravděpodobností nekonečná (nebudu se pouštět do vysvětlování proč, tak svět funguje), takže se budeme muset dobrovolně rozhodnout, že ji v určitém okamžiku přerušíme (nastavení za tímto bodem se rovná nule). To se ale nestane jen tak - důsledkem toho, jak by se dalo očekávat, bude zkreslení frekvenční charakteristiky vypočítaného filtru - bude zvlněná a frekvenční omezení bude rozmazané.
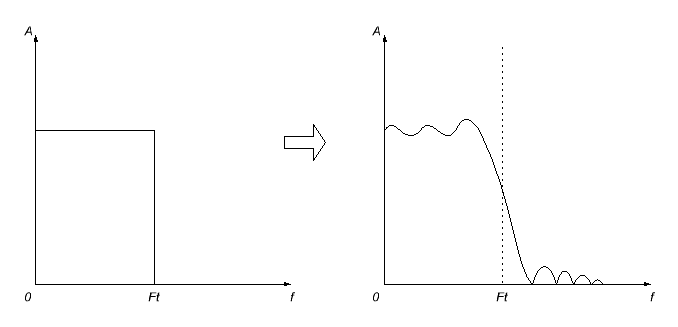
Pro minimalizaci těchto efektů jsou na zkrácenou impulsní odezvu aplikovány různé funkce vyhlazovacího okna. V důsledku toho je frekvenční charakteristika obvykle ještě více rozmazaná, ale nepříjemné (zejména v propustném pásmu) mizí. 
Ve skutečnosti po takovém zpracování získáme pracovní impulsní odezvu a můžeme sestavit digitální filtr.
Druhý způsob výpočtu je ještě jednodušší - impulsní odezvy nejoblíbenějších filtrů jsou pro nás již dlouho vyjádřeny v analytické podobě. Zbývá pouze nahradit vaše hodnoty a použít funkci okna na výsledek podle vašich představ. Nemusíte tedy ani uvažovat o žádných proměnách.
A samozřejmě, pokud je cílem emulovat chování konkrétního obvodu, můžete získat jeho impulsní odezvu v simulátoru:
Zde jsem přivedl na vstup RC obvodu impuls 100500 voltů (ano, 100,5 kV) s dobou trvání 1 μs a získal jeho impulsní odezvu. Je jasné, že ve skutečnosti to nejde, ale v simulátoru tato metoda, jak vidíte, funguje skvěle.
5. Poznámky.
To, co bylo řečeno výše o zkrácení impulsní odezvy, platilo samozřejmě pro tkzv. filtry s konečnou impulsní odezvou (FIR/FIR filtry). Mají spoustu cenných vlastností, včetně lineární fáze (za určitých podmínek pro konstrukci impulsní odezvy), která zajišťuje absenci zkreslení signálu při filtraci a také absolutní stabilitu. Existují také filtry s nekonečnou impulsní odezvou (IIR/IIR filtry). Jsou méně náročné na zdroje, pokud jde o výpočty, ale již nemají uvedené výhody.
V příštím článku se doufám podívám na jednoduchý příklad praktické implementace digitálního filtru.
STÁTNÍ TECHNICKÁ UNIVERZITA NOVOSIBIRSK
FAKULTA AUTOMATIZACE A POČÍTAČE
Katedra systémů sběru a zpracování dat
Disciplína "Teorie a zpracování signálů"
LABORATORNÍ PRÁCE Č.10
DIGITÁLNÍ FILTRY
S KONEČNOU IMPULZNÍ CHARAKTERISTIKOU
Skupina: AT-33
Volba: 1 Učitel:
Student: Shadrina A.V. Doc. Shchetinin Yu.I.
Cíl práce: studium metod analýzy a syntézy filtrů s konečnou impulsní odezvou pomocí funkcí vyhlazovacího okna.
Dokončení díla:
1. Grafy impulsní odezvy dolní propusti FIR filtru s pravoúhlou mezní frekvencí okna pro hodnoty délky filtru a .
Impulzní odezva ideálního diskrétního FIR filtru má nekonečnou délku a je nenulová pro záporné hodnoty:
.
Abychom získali fyzicky proveditelný filtr, měli bychom omezit impulsní odezvu na konečné číslo a poté zkrácenou odezvu posunout o určitou hodnotu doprava.
Hodnota je délka (velikost) filtru, 
– pořadí filtrů.
Matlab Script (labrab101.m)
N = input("Zadejte délku filtru N = ");
h = sin(wc.*(n-(N-1)/2))./(pi.*(n-(N-1)/2));
xlabel("Referenční číslo, n")
>> podkres (2,1,1)
>> labrab101
Zadejte délku filtru N = 15
>> title("Impulzní odezva FIR filtru pro N=15")
>> podkres (2,1,2)
>> labrab101
Zadejte délku filtru N = 50
>> title("Impulzní odezva FIR filtru pro N=50")
Obr. 1. Grafy impulsní odezvy dolní propusti FIR filtru s pravoúhlou mezní frekvencí okna pro hodnoty délky filtru a
komentář: Pokud vezmeme v úvahu frekvenční odezvu digitálního filtru jako Fourierovu řadu: 
, pak koeficienty této řady budou představovat hodnoty impulsní odezvy filtru. V tomto případě byla Fourierova řada zkrácena v prvním případě na , a ve druhém - na a poté byly zkrácené charakteristiky posunuty podél osy vzorku doprava, aby se získal kauzální filtr. Když je šířka hlavního laloku 2, a když - 1, tzn. S rostoucí délkou filtru se hlavní lalok impulsní odezvy zužuje. Uvažujeme-li úroveň postranních laloků (pomocí ), tak se zvyšováním roste v absolutní hodnotě od do . Můžeme tedy dojít k závěru, že při použití aproximace ideální frekvenční odezvy filtru s pravoúhlým oknem není možné současně zúžit hlavní lalok (a tím zmenšit přechodovou oblast) a snížit úrovně postranních laloků (snížit zvlnění v propustném pásmu a zádržném pásmu filtru). Jediným ovladatelným parametrem obdélníkového okna je jeho velikost, kterou lze ovlivnit šířku hlavního laloku, na boční laloky to však příliš neovlivňuje.
2. Výpočet DVFT impulsních charakteristik z kroku 1 pomocí funkce. Grafy jejich frekvenční charakteristiky na lineární stupnici a v decibelech pro 512 frekvenční vzorky. Propustné pásmo, přechodové pásmo a stop pásmo filtru. Vliv pořadí filtru na šířku přechodového pásma a úroveň zvlnění frekvenční odezvy v propustném a koncovém pásmu.
Funkce Matlab (DTFT.m)
funkce = DTFT(x,M)
N = max (M, délka (x));
% Zmenšení FFT na velikost 2^m
N = 2^(ceil(log(N)/log(2)));
% Vypočítejte fft
% Vektor frekvence
w = 2*pi*((0:(N-l))/N);
w = w - 2*pi*(w>=pi);
% Shift FFT na rozsah od -pi do +pi
X = fftshift(X);
w = fftshift(w);
Matlab Script (labrab102.m)
h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));
h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));
DTFT(h1,512);
DTFT(h2,512);
plot(w./(2*pi),abs(H1)./max(abs(H1)),,"r")
xlabel("f, Hz"), ylabel("|H1|/max(|H1|)")), mřížka
plot(w./(2*pi),abs(H2)./max(abs(H2)),,"b")
xlabel("f, Hz"), ylabel("|H2|/max(|H2|)")), mřížka
plot(w./(2*pi),20*log10(abs(H1)),,"r")
title("Kmitočtová odezva dolní propusti FIR filtru s obdélníkovým oknem pro N = 15")
xlabel("f, Hz"), ylabel("20lg(|H1|), dB"), mřížka
plot(w./(2*pi),20*log10(abs(H2)),"b")
title("Kmitočtová odezva dolní propusti FIR filtru s obdélníkovým oknem pro N = 50")
xlabel("f, Hz"), ylabel("20lg(|H2|), dB"), mřížka
Obr.2. Grafy frekvenční odezvy dolnopropustného FIR filtru s pravoúhlou mezní frekvencí okna pro hodnoty délky filtru a na lineární stupnici
Obr.3. Grafy frekvenční odezvy dolnopropustného FIR filtru s pravoúhlou mezní frekvencí okna pro hodnoty délky filtru a na logaritmické stupnici
komentář:
Stůl 1. Rozsah propustného pásma, přechodové oblasti a stoppásma pro délku filtru a
|
Délka filtru |
Šířka pásma, Hz |
Přechodová oblast, Hz |
Stop pásmo, Hz |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Přednáška č. 10 "Digitální filtry s konečnou impulsní odezvou" Přenosová funkce fyzicky realizovatelného digitálního filtru s konečnou impulsní odezvou (FIR filtr) může být reprezentována jako (10.1). Při nahrazení ve výrazu (10.1) získáme frekvenční charakteristiku FIR filtru ve tvaru Kde Fázové zpoždění filtr je definován jako Skupinové zpoždění filtr je definován jako Výraznou vlastností FIR filtrů je schopnost implementovat konstantní fázová a skupinová zpoždění, tzn. lineární fázová odezva (10.5), kde - konstantní. Pokud je tato podmínka splněna, signál procházející filtrem nezkresluje jeho tvar. Pro odvození podmínek, které zajišťují lineární fázovou odezvu, zapíšeme frekvenční charakteristiku FIR filtru s přihlédnutím k (10.5) Porovnáním skutečné a imaginární části této rovnosti dostaneme Vydělením druhé rovnice první dostaneme Konečně můžeme psát Tato rovnice má dvě řešení. Nejprve kdy A =0 odpovídá rovnici Tato rovnice má jedinečné řešení odpovídající libovolnému h (0) (sin (0) = 0) a h (n) = 0 pro n >0. Toto řešení odpovídá filtru, jehož impulsní odezva má v počátečním čase jeden nenulový vzorek. Takový filtr není praktický. Najdeme jiné řešení pro . V tomto případě křížovým násobením čitatelů a jmenovatelů v (10.8) dostaneme (10.11). Odtud máme Protože tato rovnice má tvar Fourierovy řady, její řešení, pokud existuje, je jedinečné. Je snadné vidět, že řešení této rovnice musí splňovat podmínky (10.13), (10.14). Z podmínky (10.13) vyplývá, že pro každou objednávku filtru N existuje pouze jedno fázové zpoždění A , při kterém lze dosáhnout přísné linearity fázové odezvy. Z podmínky (10.14) vyplývá, že impulsní odezva filtru musí být symetrická k bodu pro liché N a vzhledem ke středu intervalu (obr. 10.1).
Frekvenční odezva takového filtru (pro liché N ) lze zapsat ve tvaru (10.15). Provedení náhrady ve druhé částce m = N -1- n , dostáváme (10.16). Protože h (n) = h (N -1- n ), pak lze tyto dva součty kombinovat Nahrazení, dostáváme (10.18). Pokud určíme tak konečně můžeme psát Tedy pro filtr s lineární fázovou odezvou máme Pro případ sudého N podobně to budeme mít my Provedením substituce ve druhém součtu dostaneme Provedením střídání, dostáváme (10.24). Po určení konečně budeme mít Tedy pro FIR filtr s lineární fázovou odezvou a rovnoměrným řádem N lze psát V následujícím budeme pro zjednodušení uvažovat pouze filtry s lichým pořadím. Při syntéze funkce přenosu filtru jsou výchozími parametry zpravidla požadavky na frekvenční charakteristiku. Existuje mnoho technik pro syntézu FIR filtrů. Podívejme se na některé z nich. Protože frekvenční odezva jakéhokoli digitálního filtru je periodickou funkcí frekvence, může být reprezentována jako Fourierova řada kde koeficienty Fourierovy řady jsou stejné Je vidět, že koeficienty Fourierovy řady h(n ) se shodují s koeficienty impulsní odezvy filtru. Pokud je tedy znám analytický popis požadované frekvenční charakteristiky filtru, je možné snadno určit koeficienty impulsní odezvy a z nich přenosovou funkci filtru. V praxi to však není možné, protože impulsní odezva takového filtru má nekonečnou délku. Navíc takový filtr není fyzicky realizovatelný, protože impulsní odezva začíná na -¥ a žádné konečné zpoždění neučiní tento filtr fyzicky realizovatelným. Jednou z možných metod pro získání FIR filtru, který se blíží dané frekvenční odezvě, je zkrátit nekonečnou Fourierovu řadu a impulsní odezvu filtru za předpokladu, že h (n) = 0 při . Pak Fyzikální realizovatelnost přenosové funkce Hz ) lze dosáhnout násobením H(z) na . Kde (10.32). Při takové úpravě přenosové funkce se amplitudová charakteristika filtru nemění a skupinové zpoždění se zvyšuje o konstantní hodnotu. Jako příklad si spočítejme dolní propust FIR filtr s frekvenční charakteristikou tvaru V souladu s (10.29) jsou koeficienty impulsní odezvy filtru popsány výrazem Nyní z (10.31) můžeme získat výraz pro přenosovou funkci Kde (10.36). Amplitudové charakteristiky vypočteného filtru pro různé N jsou uvedeny na obr. 10.2.
Obr.10.2 Zvlnění v propustném pásmu a stoppásmu nastává v důsledku pomalé konvergence Fourierovy řady, která je zase způsobena přítomností diskontinuity ve funkci na mezní frekvenci propustného pásma. Tyto pulzace jsou známé jako Gibbs se vlní. Z obr. 10.2 je zřejmé, že s rostoucí N frekvence pulsace se zvyšuje a amplituda klesá při nižších i vyšších frekvencích. Amplituda posledního zvlnění v propustném pásmu a prvního zvlnění v propustném pásmu však zůstávají prakticky nezměněny. V praxi jsou takové účinky často nežádoucí, což vyžaduje nalezení způsobů, jak snížit Gibbsovy pulsace. Zkrácená impulsní odezva h(n ) lze reprezentovat jako součin požadované nekonečné impulsní odezvy a některých funkce okna w (n) délky n (obr. 10.3).
V uvažovaném případě prostého zkrácení Fourierovy řady použijeme obdélníkové okno V tomto případě může být frekvenční charakteristika filtru reprezentována jako komplexní konvoluce To znamená, že půjde o „rozmazanou“ verzi požadované charakteristiky. Problém spočívá v nalezení funkcí okna, které umožňují snížit Gibbsovo zvlnění se stejnou selektivitou filtru. Chcete-li to provést, musíte nejprve prostudovat vlastnosti funkce okna na příkladu obdélníkového okna. Spektrum funkce obdélníkového okna lze zapsat jako Spektrum funkce obdélníkového okna je uvedeno na obr. 10.4.
Obr.10.4 Protože v , šířka hlavního laloku spektra se ukáže být rovna . Přítomnost postranních laloků ve spektru funkce okna vede ke zvýšení Gibbsova zvlnění ve frekvenční odezvě filtru. Pro dosažení nízkého zvlnění v propustném pásmu a vysokého útlumu v ochranném pásmu je nutné, aby oblast omezená bočními laloky byla malým zlomkem plochy omezené hlavním lalokem. Šířka hlavního laloku zase určuje šířku přechodové zóny výsledného filtru. Pro vysokou selektivitu filtru by měla být šířka hlavního laloku co nejmenší. Jak je z výše uvedeného patrné, šířka hlavního laloku se s rostoucím řádem filtru zmenšuje. Vlastnosti vhodných okenních funkcí lze tedy formulovat následovně: - funkce okna musí být časově omezena; - spektrum funkce okna by se mělo nejlépe přibližovat funkci frekvenčně omezené, tzn. mít minimum energie mimo hlavní lalok; - Šířka hlavního laloku spektra funkcí okna by měla být co nejmenší. Nejčastěji používané funkce okna jsou: 1. Obdélníkové okno. Diskutováno výše. 2. Hammingovo okno. kde . Toto okno se nazývá Hannovo okno ( hanning). 3. Blackmanovo okno. 4. Bartlettovo okno. Indikátory filtrů vytvořených pomocí specifikovaných funkcí okna jsou shrnuty v tabulce 10.1.
Faktor zvlnění je definován jako poměr maximální amplitudy postranního laloku k amplitudě hlavního laloku ve spektru funkce okna. Chcete-li vybrat požadované pořadí filtrů a nejvhodnější funkci okna při výpočtu skutečných filtrů, můžete použít údaje v tabulce 10.2.
Jak je vidět z tabulky 10.1, existuje určitý vztah mezi koeficientem zvlnění a šířkou hlavního laloku ve spektru funkce okna. Čím menší je koeficient pulsace, tím větší je šířka hlavního laloku, a tedy i přechodové zóny ve frekvenční odezvě filtru. Pro zajištění nízkého zvlnění v propustném pásmu je nutné zvolit okno s vhodným koeficientem zvlnění a zajistit požadovanou šířku přechodové zóny se zvýšeným řádem filtru N. Tento problém lze vyřešit pomocí okna navrženého Kaiserem. Funkce okna Kaiser má tvar
kde a je nezávislý parametr,
Atraktivní vlastností Kaiserova okna je možnost plynule měnit koeficient pulzace z malých na velké hodnoty, přičemž se mění pouze jeden parametr a. V tomto případě, stejně jako u jiných funkcí okna, lze šířku hlavního laloku upravit pořadím filtru N. Hlavní parametry nastavené při vývoji skutečného filtru jsou: Šířka pásma - w p ; Překážkový pás - w a ; Maximální přípustné zvlnění v propustném pásmu je A p ; Minimální útlum stoppásma – A a ; -vzorkovací frekvence - ws. Tyto parametry jsou znázorněny na obr. 10.5. V tomto případě je maximální zvlnění v propustném pásmu určeno jako
a minimální útlum v dorazovém pásmu je as Poměrně jednoduchý postup pro výpočet filtru s oknem Kaiser zahrnuje následující kroky: 1. Stanoví se impulsní odezva filtru h (n), pokud je frekvenční odezva ideální
kde (10,49). 2. Parametr d je vybrán jako
Kde 3. Skutečná hodnota A a a A p se vypočte pomocí vzorců (10.46), (10.47). 4.Parametr a je vybrán jako
5.Parametr D je vybrán jako
6. Z podmínky vyberte nejmenší lichou hodnotu pořadí filtrů
to následuje Protože vzorky impulsní odezvy filtru jsou koeficienty jeho přenosové funkce, podmínka (10.59) znamená, že kódy všech koeficientů filtru obsahují pouze zlomkovou část a znaménkový bit a neobsahují celočíselnou část. Počet číslic zlomkové části koeficientů filtru je určen z podmínky splnění filtrační přenosové funkce s kvantovanými koeficienty, zadaných požadavků na přiblížení se referenční přenosové funkci s přesnými hodnotami koeficientů. Absolutní hodnoty vzorků vstupního signálu filtru jsou obvykle normalizovány tak, že Pokud se analýza provádí pro FIR filtr s lineární fázovou odezvou, pak může být algoritmus pro výpočet jeho výstupního signálu následující kde jsou koeficienty filtru zaokrouhleny na s k. Tento algoritmus odpovídá blokovému schématu filtru na obr. 10.5.
Existují dva způsoby, jak implementovat tento algoritmus. V prvním případě jsou všechny operace násobení prováděny přesně a nedochází k zaokrouhlování součinů. V tomto případě je bitová hloubka produktů rovna s v +s k, kde s in je bitová hloubka vstupního signálu a sk je bitová hloubka koeficientů filtru. V tomto případě blokové schéma filtru znázorněné na obr. 10.5 přesně odpovídá skutečnému filtru. Ve druhém způsobu implementace algoritmu (10.61) je každý výsledek operace násobení zaokrouhlen, tzn. produkty jsou počítány s určitou chybou. V tomto případě je nutné změnit algoritmus (10.61) tak, aby zohlednil chybu způsobenou zaokrouhlením produktů Pokud jsou vzorkové hodnoty výstupního signálu filtru vypočteny pomocí první metody (s přesnými hodnotami produktů), pak se rozptyl výstupního šumu určí jako
těch. závisí na rozptylu zaokrouhlovacího šumu vstupního signálu a hodnotách koeficientů filtru. Zde můžete zjistit požadovaný počet bitů vstupního signálu jako
Pomocí známých hodnot sin a sk lze určit počet bitů potřebných pro zlomkovou část kódu výstupního signálu jako Pokud jsou hodnoty vzorků výstupního signálu vypočítány pomocí druhé metody, kdy je každý součin zaokrouhlen na s d číslic, pak lze rozptyl zaokrouhlovacího šumu vytvořeného každým z násobičů vyjádřit jako počet číslic produkt jako DR vstup a odstup signálu od šumu na výstupu filtru SNR out. Dynamický rozsah vstupního signálu v decibelech je definován jako
kde A max a A min jsou maximální a minimální amplitudy vstupního signálu filtru. Poměr signálu k šumu na výstupu filtru, vyjádřený v decibelech, je definován jako
určuje střední kvadraturu výkonu výstupního sinusového signálu filtru s amplitudou A min a (10.77) určuje sílu šumu na výstupu filtru. Z (10,75) a (10,76) s A max =1 získáme výraz pro rozptyl šumu na výstupu filtru Tuto hodnotu rozptylu šumu na výstupu filtru lze použít k výpočtu bitové hloubky vstupních a výstupních signálů filtru.  Svět bezplatných programů a užitečných tipů 2024 whatsappss.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(10.2),
- amplitudově-frekvenční odezva (AFC) filtr,
- fázově-frekvenční odezva (PFC) filtr.
(10.3).
(10.4).
(10.6).
(10.7).
(10.8).
(10.9).
(10.10).
(10.12).
(10.17).
(10.19),
(10.20).
(10.21).
(10.22).
(10.23).
(10.25),
(10.26).
(10.27).
(10.28),
(10.29).
(10.30).
(10.31),
(10.33).
(10.34).
(10.35),
(10.37).
(10.38).
(10.39).
(10.40).
(10.41),
(10.42).
(10.43).
(10.44),
, I 0 – Besselova funkce prvního druhu nultého řádu, definovaná výrazem
(10.45).
(10.46),
(10.50),
(10.51).
(10.52).
(10.53).
(10.54),
(10.57)
(10.66),
(10.67).
(10.74),
(10.75),
(10.78).