Impulsni odziv filtera. Digitalni filteri sa konačnim impulsnim odzivom. Izglađivanje podataka. Filtriranje medijana
48 Digitalni filteri sa konačnim impulsnim odzivom. Proračun kih filtera.
Filter s konačnim impulsnim odzivom (Nerekurzivni filter, FIR filter) ili FIR filter (FIR je skraćeno od konačni impulsni odziv - konačni impulsni odziv) - jedan od tipova linearnih digitalnih filtara, čija je karakteristična karakteristika njegovo vremensko ograničenje impulsni odgovor(od nekog trenutka postaje tačno jednako nuli). Takav filter se naziva i nerekurzivnim zbog nedostatka povratne sprege. Nazivnik prijenosne funkcije takvog filtera je određena konstanta.
Jednačina razlike koja opisuje odnos između ulaznih i izlaznih signala filtera: gdje P- red filtera, x(n) - ulazni signal, y(n) je izlazni signal, i b i- koeficijenti filtera. Drugim riječima, vrijednost bilo kojeg uzorka izlaznog signala određena je zbirom skaliranih vrijednosti P prethodna čitanja. Možete to reći drugačije: vrijednost izlaza filtera u bilo kojem trenutku je vrijednost odgovora na trenutnu vrijednost ulaza i zbroj svih postupno opadajućih odgovora P prethodni uzorci signala koji i dalje utiču na izlaz (nakon P-counts, funkcija prijelaza impulsa postaje jednaka nuli, kao što je već spomenuto, dakle svi članovi nakon toga P-th će takođe postati jednak nuli). Zapišimo prethodnu jednačinu u opširnijem obliku:
Da pronađemo jezgro filtera stavljamo
x(n) = δ( n)
gdje je δ( n) - delta funkcija. Tada se impulsni odziv FIR filtera može zapisati kao:
Z-transformacija impulsnog odziva daje nam funkciju prijenosa FIR filtera:
]Svojstva
FIR filter ima niz korisnih svojstava zbog kojih je ponekad poželjniji za upotrebu od IIR filtera. Evo nekih od njih:
FIR filteri su robusni.
FIR filteri ne zahtijevaju povratnu informaciju kada se implementiraju.
Fazu FIR filtera možemo učiniti linearnom
Direktan oblik FIR filtera
FIR filteri se mogu implementirati pomoću tri elementa: množitelja, sabirača i bloka kašnjenja. Opcija prikazana na slici je direktna implementacija FIR filtera tipa 1.
Implementacija direktnog oblika FIR filtera
Primjer programa
Ispod je primjer programa FIR filtera napisanog u C:
/* FIR filter za 128 slavina */
float fir_filter (float input)
statički plutajući uzorak;
acc = 0.0f; /* Baterija */
/* Množite i akumulirajte */
za (i = 0; i< 128; i++) {
acc += (h[i] * uzorak[i]);
/* Izlaz */
/* Pomaknite odloženi signal */
za (i = 127; i > 0; i--)
uzorak[i] = uzorak;
49 Izglađivanje podataka. Pokretno prosječenje.
50 Izglađivanje podataka. Parabolično zaglađivanje.
51 Izglađivanje podataka. Spencer zaglađivanje.
52 Izglađivanje podataka. Filtriranje medijana.
Pokretno usrednjavanje, parabolično izglađivanje, Spencerovo izglađivanje, srednje filtriranje
Prilikom razvoja metoda za određivanje parametara fizičkih procesa koji se sporo mijenjaju tokom vremena, važan zadatak je eliminisanje utjecaja šumnih efekata ili slučajnih smetnji koje se superponiraju na obrađeni signal primljen na izlazu primarnog pretvarača.
Da biste eliminirali ovaj efekat, možete primijeniti izglađivanje podataka. Jedna od najjednostavnijih metoda takvog izglađivanja je aritmetičko usrednjavanje. Kada se koristi, svaka vrijednost diskretne funkcije (niza obrađenih podataka) izračunava se u skladu s izrazom:
gdje je broj bodova za aritmetički prosjek (neparan cijeli broj);
Vrijednost funkcije prije obrade;
Postoje i druge prilično efikasne metode zaglađivanja, na primjer, sa parabolama drugog stepena na pet, sedam, devet i jedanaest tačaka u skladu sa izrazima:
ili parabole četvrtog stepena u sedam, devet, jedanaest i trinaest tačaka:
U praktičnim primjenama, druge efikasne metode, na primjer, Spencerovo zaglađivanje u 15 tačaka, daju dobre rezultate:
Zamjenom kompleksnog eksponencijala gdje u ove izraze možemo odrediti prijenosnu funkciju odgovarajuće transformacije.
Za aritmetičko usrednjavanje
Izraz u zagradi predstavlja geometrijsku progresiju sa nazivnikom, stoga se ovaj izraz može predstaviti kao:
.
Ova formula predstavlja prijenosnu karakteristiku niskopropusnog filtera i pokazuje da što je više članova uključeno u usrednjavanje, to je veća supresija visokofrekventnih komponenti šuma u signalu (vidi sliku 6.1).
Međutim, semantički koncept frekvencije prilikom obrade vremenskih trendova razlikuje se od sličnog koncepta prilikom obrade signala. To se objašnjava činjenicom da pri proučavanju vremenskih trendova nije interesantan njihov frekventni sastav, već vrsta promjene (povećanje, smanjenje, konstantnost, cikličnost, itd.).
Upotreba takozvanih heurističkih algoritama je takođe prilično efikasna za izglađivanje podataka.
Jedan od njih je srednje filtriranje. Prilikom implementacije u kliznom vremenskom prozoru dimenzije , gdje je cijeli broj neparan broj, centralni element zamjenjuje se srednjim elementom niza, kojima su poredani, uzlaznim redoslijedom vrijednosti, elementi niza podataka izglađenog signal pada unutar vremenskog okvira. Prednost srednjeg filtriranja je mogućnost uklanjanja impulsnog šuma, čije trajanje ne prelazi, praktično bez izobličenja signala koji se glatko mijenjaju. Ova metoda suzbijanja buke nema strogo matematičko opravdanje, ali jednostavnost proračuna i efektivnost dobijenih rezultata doveli su do njegove široke upotrebe.
Slika 6.1 - Grafovi karakteristika prijenosa
Operacije aritmetičkog usrednjavanja za m=5, 7, 9, 11
Još jedan zanimljiv algoritam izglađivanja je prosječenje medijane. Njegova suština je sljedeća. U kliznom vremenskom prozoru veličine (-neparan cijeli broj), elementi niza podataka su poredani uzlaznim redoslijedom, a zatim se prvi i posljednji element uklanjaju iz uređenog niza (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
Ova metoda vam omogućava da potisnete pulsne i radiofrekventne smetnje, kao i da postignete dobro izglađivanje signala.
| " |
Razmotrimo najjednostavniji digitalni filter - filtere sa konstantnim parametrima.
Ulazni signal digitalnog filtera isporučuje se u obliku niza numeričkih vrijednosti koje slijede u intervalima (slika 4.1, a). Kada se svaka sljedeća vrijednost signala primi u digitalni filter, izračunava se sljedeća vrijednost izlaznog signala.Algoritmi proračuna mogu biti vrlo raznoliki; tokom procesa proračuna, osim posljednje vrijednosti ulaznog signala, može se koristiti
prethodne vrijednosti ulaznih i izlaznih signala: Izlazni signal digitalnog filtera je također niz numeričkih vrijednosti koji prate interval od . Ovaj interval je isti za cijeli uređaj za digitalnu obradu signala.
Rice. 4.1. Signal na ulazu i izlazu digitalnog filtera
Stoga, ako primijenite najjednostavniji signal u obliku jednog impulsa na ulaz digitalnog filtera (slika 4.2, a)
tada na izlazu dobijamo signal u obliku diskretnog niza numeričkih vrijednosti, koji slijede u intervalima
Po analogiji sa konvencionalnim analognim kolima, ovaj signal odziva ćemo nazvati impulsnim odzivom filtera (slika 4.2, b). Za razliku od impulsnog odziva analognog kola, funkcija je bezdimenzionalna.
Rice. 4.2. Jedinični impuls i impulsni odziv digitalnog filtera
Primijenimo proizvoljan diskretni signal na ulaz filtera (sl. 4.1, a), koji je skup diskretnih vrijednosti
Pod dejstvom prvog elementa, niz pomnožen sa formira se na izlazu filtera; pod dejstvom, sekvenca se množi sa i pomera udesno za iznos, itd. Kao rezultat, izlaz će dobiti redosled gde
Dakle, izlazni signal je definiran kao diskretna konvolucija ulaznog signala i impulsnog odziva. U tom pogledu, digitalni filteri su slični konvencionalnim kolima, gdje je izlazni signal jednak konvoluciji ulaznog signala i impulsnog odziva.
Formula (4.1) je algoritam digitalnog filtriranja. Ako je impulsni odziv filtera opisan nizom sa konačnim brojem članova, tada se filter može implementirati u obliku kola prikazanog na Sl. 4.3. Ovdje slovo označava elemente kašnjenja signala za vrijeme (po ćeliji); -elementi koji množe signal sa odgovarajućim koeficijentom.
Dijagram prikazan na sl. 4.3 nije električno kolo digitalnog filtera; Ovaj dijagram je grafički prikaz algoritma digitalnog filtriranja i prikazuje redoslijed aritmetičkih operacija koje se izvode tokom obrade signala.
Rice. 4.3. Nerekurzivni digitalni filterski krug
Za digitalne filtere koji obrađuju signale u obliku apstraktnih numeričkih nizova, koncept “vremenskog kašnjenja” nije sasvim ispravan. Stoga su elementi koji odlažu signal za jednu ćeliju obično označeni na krugovima digitalnog filtera simbolom koji označava kašnjenje signala na jeziku -transformacija. U nastavku ćemo se pridržavati ove notacije.
Vratimo se na krug digitalnog filtera prikazan na sl. 4.3, Takvi filteri, u kojima se za proračun koriste samo vrijednosti ulaznog signala, nazivaju se jednostavnim ili nerekurzivnim.
Algoritam nerekurzivnog filtera je lako napisati ako je poznat impulsni odziv filtera. Za praktičnu implementaciju algoritma potrebno je da impulsni odziv sadrži konačan broj članova. Ako impulsni odziv sadrži beskonačan broj pojmova, ali oni brzo smanjuju vrijednost, tada se možete ograničiti na konačan broj pojmova, odbacujući one čije su vrijednosti male. Ako elementi impulsnog odziva ne opadaju u vrijednosti, algoritam nerekurzivnog filtera se ispostavlja neostvarivim.
Rice. 4.4. -lanac
Kao primjer, razmotrite najjednostavniji digitalni filter, sličan -kolu (slika 4.4). Impulsni odziv kola ima oblik
Da biste zapisali impulsni odziv odgovarajućeg digitalnog filtera, izraz treba zamijeniti sa. Međutim, impulsni odziv kola ima dimenziju, a impulsni odziv digitalnog filtera mora biti bezdimenzionalni. Stoga izostavljamo množitelj u izrazu (4.2) i zapisujemo impulsni odziv digitalnog filtera u obliku
Takav impulsni odziv sadrži beskonačno mnogo pojmova, ali njihova veličina opada prema eksponencijalnom zakonu i možemo se ograničiti na termine, birajući takve da
Sada možemo napisati izraz za signal na izlazu filtera
Ovaj izraz je takođe algoritam digitalnog filtera. Dijagram ovog filtera je prikazan na sl. 4.5.
Drugi pristup analizi procesa u digitalnim filterima sličan je operatorskoj metodi analize konvencionalnih analognih kola, samo što se umjesto Laplaceove transformacije koristi -transformacija.
Rice. 4.5. Krug nerekurzivnog digitalnog filtera sličan -krugu
Definirajmo parametar digitalnog filtera sličan prijenosnoj funkciji električnog kola. Da biste to učinili, primijenite transformaciju na impulsni odziv digitalnog filtera:
Funkcija se zove funkcija sistemskog filtera.
U skladu sa izrazom (4.1), signal na izlazu digitalnog filtera jednak je diskretnoj konvoluciji ulaznog signala i impulsnom odzivu filtera. Primjenom teoreme konvolucije na ovaj izraz, dobivamo da je transformacija izlaznog signala jednaka transformaciji ulaznog signala pomnoženoj sa funkcijom filtera sistema:
Dakle, funkcija sistema igra ulogu prijenosne funkcije digitalnog filtera.
Kao primjer, pronađimo sistemsku funkciju digitalnog filtera prvog reda sličnu -krugu:
Treća metoda analize prolaska signala kroz digitalne filtere slična je klasičnoj metodi diferencijalnih jednačina. Razmotrimo ovu metodu koristeći lance narudžbi kao primjer.
Najjednostavniji analogni krug 1. reda je -kolo (vidi sliku 4.4), prolaz signala kroz koji je opisan diferencijalnom jednadžbom
Za diskretno kolo, umjesto diferencijalne jednadžbe (4.8), treba napisati diferencijsku jednačinu u kojoj su ulazni i izlazni signali specificirani za diskretne trenutke vremena, a umjesto derivacije razlika vrijednosti susjednih signala pojaviti. Za diskretno kolo prvog reda, jednadžba razlike može se napisati u prilično općenitom obliku
Primijenimo transformaciju na jednadžbu
gdje nalazimo funkciju filtera sistema
Formula (4.10) je prilično opšti izraz za sistemsku funkciju digitalnog filtera 1. reda. Kada se poklapa sa prethodno dobijenim izrazom (4.7) za sistemsku funkciju digitalnog filtera ekvivalentnog -kolu.
Nađimo algoritam digitalnog filtriranja koji odgovara sistemskoj funkciji (4.10). Da bismo to učinili, rješavamo jednačinu (4.9) za
Ekvivalentni dijagram ovog algoritma prikazan je na Sl. 4.6. U poređenju sa nerekurzivnim filterom (vidi sliku 4.5), ovde je dodata neka vrsta „kola za povratnu spregu“, što znači da se vrednosti izlaznog signala koriste u kasnijim
Rice. 4.6. Krug rekurzivnog digitalnog filtera sličan -krugu
kalkulacije. Filteri ovog tipa nazivaju se rekurzivni.
Algoritam (4.11) odgovara filteru koji je potpuno ekvivalentan nerekurzivnom filteru razmatranom ranije. Ali da bi se pomoću algoritma nerekurzivnog filtera (4.4) odredila jedna vrijednost izlaznog signala, potrebno je izvršiti operacije, a kada se koristi algoritam rekurzivnog filtera (4.11), potrebne su samo dvije operacije. Ovo je glavna prednost rekurzivnih filtera. Osim toga, rekurzivni filteri omogućavaju obradu signala sa većom preciznošću, jer omogućavaju pravilniju implementaciju impulsnog odziva bez odbacivanja njegovog „repa“. Rekurzivni filteri vam omogućavaju da implementirate algoritme koji se uopšte ne mogu implementirati koristeći nerekurzivne filtere. Na primjer, s filterom koji radi prema krugu na sl. 4.6, je u suštini idealan akumulator-integrator i ima impulsni odziv oblika. Filter sa takvom karakteristikom ne može se implementirati upotrebom nerekurzivne šeme.
Razmatrani primjeri pokazuju da nema smisla koristiti nerekurzivne algoritme za kreiranje digitalnih filtera s dugim impulsnim odzivom. U ovim slučajevima je prikladnije koristiti rekurzivne filtere.
Područje primjene nerekurzivnih algoritama je implementacija digitalnih filtera s impulsnim odzivom koji sadrži mali broj pojmova. Primjer je najjednostavniji diferencijator čiji je izlazni signal jednak porastu ulaznog signala:
Krug takvog digitalnog filtera prikazan je na Sl. 4.7.
Rice. 4.7. Kolo najjednostavnijeg digitalnog diferencijatora
Razmotrimo sada opšti digitalni filter, koji je opisan jednadžbom
Ova jednačina se može smatrati i kao razlika jednačina reda i kao algoritam digitalnog filtriranja, ako se drugačije napiše, tj.
Rice. 4.8. Rekurzivni krug filtera digitalnog reda
Algoritam (4.13) odgovara kolu prikazanom na Sl. 4.8. Nađimo sistemsku funkciju takvog filtera. Da biste to učinili, primijenite transformaciju na jednadžbu:
Izraz (4.14) nam omogućava da uspostavimo vezu između fluktuacija elemenata filterskog kola i funkcije sistema. Koeficijenti u brojniku sistemske funkcije određuju vrijednosti koeficijenata za
(u nerekurzivnom dijelu filtera), a koeficijenti u nazivniku određuju rekurzivni dio filtera.
Sve je počelo kada je prijatelju prijatelja prijatelja trebala pomoć oko ovih istih filtera. Putem Jedi puteva do mene su stigle glasine o tome, odjavio sam se u komentarima na objavu na linku. Činilo se da pomaže. Pa, nadam se.
Ova priča mi je uzburkala uspomene na treći, ili tako nešto, naravno, kada sam i sama uzeo DSP, i potaknula me da napišem članak za sve one koje zanima kako rade digitalni filteri, ali koji se prirodno plaše preko -vrhunske formule i psihodelični crteži (već ne govorim o udžbenicima).
Općenito, prema mom iskustvu, situacija sa udžbenicima je opisana dobro poznatom frazom da se ponekad ne vidi šuma za drveće. A to će reći, kada vas odmah počnu plašiti Z-transformacijom i formulama za dijeljenje polinoma, koji su često duži od dvije ploče, interesovanje za temu izuzetno brzo prestaje. Počećemo sa jednostavnim; srećom, da bismo razumeli šta se dešava, uopšte nije potrebno opisivati dugačke složene izraze.
Dakle, prvo, nekoliko jednostavnih osnovnih pojmova.
1. Impulsni odgovor.
Recimo da imamo kutiju sa četiri igle. Nemamo pojma šta je unutra, ali sigurno znamo da su dva leva terminala ulaz, a dva desna izlaz. Pokušajmo na njega primijeniti vrlo kratak impuls vrlo velike amplitude i vidjeti šta se dešava na izlazu. Pa, nije jasno šta je unutar ovog četveropola, jer nije jasno kako to opisati, ali barem ćemo nešto vidjeti.
Ovdje se mora reći da se kratak (općenito govoreći, beskonačno kratak) impuls velike (općenito govoreći, beskonačne) amplitude u teoriji naziva delta funkcija. Usput, smiješno je da je to integralni dio ovoga beskrajno funkcija je jednaka jedan. Ovo je normalizacija.
Dakle, ono što smo vidjeli na izlazu kvadripolne mreže, primijenivši delta funkciju na ulaz, zove se impulsni odgovor ovaj četvoropol. Za sada, međutim, nije jasno kako će nam to pomoći, ali prisjetimo se dobivenog rezultata i prijeđimo na sljedeći zanimljiv koncept.
2. Konvolucija.
Ukratko, konvolucija je matematička operacija koja se svodi na integraciju proizvoda funkcija:
Kao što vidite, označeno je zvjezdicom. Također možete vidjeti da se tokom konvolucije jedna funkcija uzima u redoslijedu „naprijed“, a mi prolazimo kroz drugu „nazad prema naprijed“. Naravno, u diskretnom slučaju, koji je vredniji za čovečanstvo, konvolucija, kao i svaki integral, ide u sumiranje:
Činilo bi se kao nekakva dosadna matematička apstrakcija. Međutim, u stvari, zavežljaj je možda najmagičniji fenomen ovog svijeta, drugi po nevjerovatnosti nakon rođenja osobe, s jedinom razlikom što većina ljudi sazna odakle djeca dolaze barem do godine. osamnaest, dok o tome šta je konvolucija i zašto je korisna i nevjerovatna, ogroman dio stanovništva Zemlje nema apsolutno pojma cijeli život.
Dakle, snaga ove operacije leži u činjenici da ako je f bilo koji proizvoljni ulazni signal, a g je impulsni odziv mreže s četiri priključka, tada će rezultat konvolucije ove dvije funkcije biti sličan onome što bismo dobiti propuštanjem signala f kroz ovu mrežu sa četiri priključka.
Odnosno, impulsni odziv je potpuni odraz svih svojstava mreže sa četiri priključka u odnosu na ulazni efekat, a konvolucija ulaznog signala s njim omogućava vam da vratite odgovarajući izlazni signal. Po mom mišljenju, ovo je jednostavno neverovatno!
3. Filteri.
Možete učiniti mnogo zanimljivih stvari sa impulsnim odgovorom i konvolucijom. Na primjer, ako je signal audio, možete organizirati reverb, eho, refren, flanger i još mnogo, mnogo više; možete razlikovati i integrirati... Općenito, možete stvoriti bilo što. Za nas je sada najvažnije da se, naravno, filteri mogu lako dobiti i konvolucijom.
Sam digitalni filter je konvolucija ulaznog signala sa impulsnim odzivom koji odgovara željenom filteru.
Ali, naravno, impulsni odgovor se mora nekako dobiti. Naravno, gore smo već smislili kako to izmjeriti, ali u takvom zadatku nema smisla u tome - ako smo filter već sastavili, čemu mjeriti nešto drugo, možemo ga koristiti kakav jeste. Osim toga, najvažnija vrijednost digitalnih filtera je da oni mogu imati karakteristike koje su u stvarnosti nedostižne (ili vrlo teško postići) - na primjer, linearna faza. Dakle, ovdje uopće ne postoji način mjerenja, samo morate računati.
4. Dobivanje impulsnog odziva.
U ovom trenutku, u većini publikacija na ovu temu, autori počinju da bacaju planine Z-transformacija i razlomaka iz polinoma na čitaoca, potpuno ga zbunjujući. Neću to raditi, samo ću ukratko objasniti o čemu se sve ovo radi i zašto u praksi naprednjačkoj javnosti nije preterano potrebno.
Recimo da smo odlučili šta želimo od filtera i napravili jednačinu koja to opisuje. Zatim, da biste pronašli impulsni odziv, možete zamijeniti delta funkciju u izvedenu jednadžbu i dobiti željenu. Jedini problem je kako to učiniti, jer je delta funkcija u vremenu O region je dat lukavim sistemom, i uopšteno postoje razne vrste beskonačnosti. Tako da u ovoj fazi sve ispada užasno teško.
Tu se dešava da se sete da postoji nešto kao što je Laplasova transformacija. Samo po sebi to nije kilogram suvog grožđa. Jedini razlog zašto se to tolerira u radiotehnici je upravo činjenica da u prostoru argumentacije u koju je ova transformacija prijelaz, neke stvari zapravo postaju jednostavnije. Konkretno, ista delta funkcija koja nam je zadala toliko problema u vremenskom domenu se vrlo lako izražava - to je samo jedna!
Z-transformacija (aka Laurent transformacija) je verzija Laplaceove transformacije za diskretne sisteme.
Odnosno, primjenom Laplaceove transformacije (ili Z-transformacije, prema potrebi) na funkciju koja opisuje željeni filter, zamjenom jednog u rezultujući i povratnom transformacijom, dobijamo impulsni odziv. Zvuči lako, svako može probati. Neću rizikovati, jer, kao što je već pomenuto, Laplasova transformacija je surova stvar, posebno ona obrnuta. Ostavimo to kao krajnje sredstvo, a mi ćemo tražiti neke jednostavnije načine da dobijemo ono što tražimo. Ima ih nekoliko.
Prvo, možemo se prisjetiti još jedne zadivljujuće činjenice prirode - amplitudno-frekventne i impulsne karakteristike su međusobno povezane dobrom i poznatom Fourierovom transformacijom. To znači da možemo nacrtati bilo koji frekvencijski odziv po svom ukusu, uzeti inverznu Fourierovu transformaciju iz njega (bilo kontinuiranu ili diskretnu) i dobiti impulsni odziv sistema koji ga implementira. Ovo je jednostavno neverovatno!
To, međutim, neće proći bez problema. Prvo, impulsni odgovor koji dobijemo će najvjerovatnije biti beskonačan (neću ulaziti u objašnjenja zašto; tako svijet funkcionira), tako da ćemo morati donijeti voljnu odluku da ga u nekom trenutku prekinemo (postavljanje jednaka je nuli izvan te tačke). Ali to se neće dogoditi tek tako - posljedica toga, kao što bi se očekivalo, bit će izobličenje frekvencijskog odziva izračunatog filtera - on će postati valovit, a frekvencijska granica će biti zamućena.
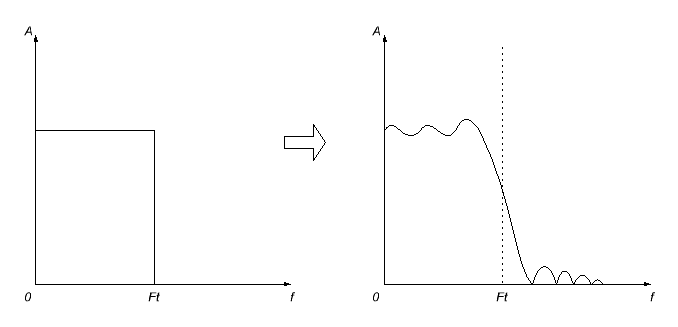
Da bi se minimizirali ovi efekti, na skraćeni impulsni odziv primjenjuju se različite funkcije prozora za izravnavanje. Kao rezultat toga, frekvencijski odziv je obično još više zamućen, ali neugodne (posebno u propusnom opsegu) oscilacije nestaju. 
Zapravo, nakon takve obrade dobijamo radni impulsni odziv i možemo napraviti digitalni filter.
Druga metoda proračuna je još jednostavnija - impulsni odzivi najpopularnijih filtara za nas su odavno izraženi u analitičkom obliku. Ostaje samo da zamenite svoje vrednosti i primenite funkciju prozora na rezultat po svom ukusu. Dakle, ne morate čak ni razmišljati o bilo kakvim transformacijama.
I, naravno, ako je cilj emulirati ponašanje određenog kola, možete dobiti njegov impulsni odgovor u simulatoru:
Ovdje sam primijenio impuls od 100500 volti (da, 100,5 kV) u trajanju od 1 μs na ulaz RC kola i dobio njegov impulsni odziv. Jasno je da se to u stvarnosti ne može učiniti, ali u simulatoru ova metoda, kao što vidite, odlično funkcionira.
5. Bilješke.
Ono što je gore rečeno o skraćivanju impulsnog odziva odnosilo se, naravno, na tzv. filteri konačnog impulsnog odziva (FIR/FIR filteri). Imaju gomilu vrijednih svojstava, uključujući linearnu fazu (pod određenim uvjetima za konstruiranje impulsnog odziva), koja osigurava odsustvo izobličenja signala tokom filtriranja, kao i apsolutnu stabilnost. Postoje i filteri beskonačnog impulsnog odziva (IIR/IIR filteri). Oni su manje resursno intenzivni u smislu proračuna, ali više nemaju navedene prednosti.
U sljedećem članku nadam se da ću pogledati jednostavan primjer praktične implementacije digitalnog filtera.
NOVOSIBIRSK DRŽAVNI TEHNIČKI UNIVERZITET
FAKULTET ZA AUTOMATIKU I RAČUNARSTVO
Odjel za sisteme prikupljanja i obrade podataka
Disciplina "Teorija i obrada signala"
LABORATORIJSKI RAD BR.10
DIGITALNI FILTERI
SA KARAKTERISTIKOM KONAČNOG IMPUSA
Grupa: AT-33
Opcija: 1 Učitelju:
student: Shadrina A.V. vanr. Shchetinin Yu.I.
Cilj rada: proučavanje metoda za analizu i sintezu filtara s konačnim impulsnim odzivom korištenjem funkcije prozora za izravnavanje.
Završetak radova:
1. Grafike impulsnog odziva niskopropusnog FIR filtera sa graničnom frekvencijom pravokutnog prozora za vrijednosti dužine filtera i .
Impulsni odziv idealnog diskretnog FIR filtera ima beskonačnu dužinu i nije nula za negativne vrijednosti:
.
Da bi se dobio fizički izvodljiv filter, treba ograničiti impulsni odziv na konačan broj, a zatim pomaknuti skraćeni odgovor udesno za određeni iznos.
Vrijednost je dužina (veličina) filtera, 
– red filtera.
Matlab skripta (labrab101.m)
N = input("Unesite dužinu filtera N = ");
h = sin(wc.*(n-(N-1)/2))./(pi.*(n-(N-1)/2));
xlabel("Referentni broj, n")
>> podzaplet (2,1,1)
>> labrab101
Unesite dužinu filtera N = 15
>> title("Impulsni odziv FIR filtera za N=15")
>> podzaplet (2,1,2)
>> labrab101
Unesite dužinu filtera N = 50
>> title("Impulsni odziv FIR filtera za N=50")
Fig.1. Grafike impulsnog odziva niskopropusnog FIR filtera sa graničnom frekvencijom pravokutnog prozora za vrijednosti dužine filtera i
Komentar: Ako uzmemo u obzir frekvencijski odziv digitalnog filtera kao Fourierov niz: 
, tada će koeficijenti ove serije predstavljati vrijednosti impulsnog odziva filtera. U ovom slučaju, Fourierov niz je skraćen u prvom slučaju na , au drugom - na , a zatim su skraćene karakteristike pomaknute duž ose uzorka udesno kako bi se dobio kauzalni filter. Kada je širina glavnog režnja 2, a kada - 1, tj. Kako se dužina filtera povećava, glavni režanj impulsnog odziva se sužava. Ako uzmemo u obzir razinu bočnih režnjeva (pomoću ), onda s povećanjem raste u apsolutnoj vrijednosti od do . Dakle, možemo zaključiti da kada se koristi aproksimacija idealnog frekvencijskog odziva filtera s pravokutnim prozorom, nemoguće je istovremeno suziti glavni režanj (i time smanjiti prijelazno područje) i smanjiti nivoe bočnih režnjeva (smanjiti talasanje u propusnom opsegu i zaustavnom pojasu filtera). Jedini parametar pravokutnog prozora koji se može kontrolirati je njegova veličina, s kojom možete utjecati na širinu glavnog režnja, ali nema mnogo utjecaja na bočne režnjeve.
2. Izračunavanje DVFT karakteristika impulsa iz koraka 1 korištenjem funkcije. Grafikoni njihovog frekvencijskog odziva na linearnoj skali iu decibelima za 512 frekvencijski uzorci. Propusni pojas, prelazni pojas i zaustavni pojas filtera. Utjecaj reda filtera na širinu prijelaznog pojasa i nivo mreškanja frekvencijskog odziva u prolaznom i zaustavnom pojasu.
Matlab funkcija (DTFT.m)
funkcija = DTFT(x,M)
N = max(M, dužina(x));
% Smanjenje FFT-a na veličinu 2^m
N = 2^(ceil(log(N)/log(2)));
% Izračunajte fft
% Vektor frekvencije
w = 2*pi*((0:(N-1))/N);
w = w - 2*pi*(w>=pi);
% Pomaknite FFT za raspon od -pi do +pi
X = fftshift(X);
w = fftshift(w);
Matlab skripta (labrab102.m)
h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));
h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));
DTFT(h1,512);
DTFT(h2,512);
plot(w./(2*pi),abs(H1)./max(abs(H1)),,"r")
xlabel("f, Hz"), ylabel("|H1|/max(|H1|)"), mreža
plot(w./(2*pi),abs(H2)./max(abs(H2)),,"b")
xlabel("f, Hz"), ylabel("|H2|/max(|H2|)"), mreža
plot(w./(2*pi),20*log10(abs(H1)),,"r")
title("Frekvencijski odziv niskopropusnog FIR filtera sa pravokutnim prozorom za N = 15")
xlabel("f, Hz"), ylabel("20lg(|H1|), dB"), mreža
plot(w./(2*pi),20*log10(abs(H2)),"b")
title("Frekvencijski odziv niskopropusnog FIR filtera s pravokutnim prozorom za N = 50")
xlabel("f, Hz"), ylabel("20lg(|H2|), dB"), mreža
Fig.2. Grafike frekvencijskog odziva niskopropusnog FIR filtera s pravokutnom graničnom frekvencijom prozora za vrijednosti dužine filtera i na linearnoj skali
Fig.3. Dijagrami frekvencijskog odziva niskopropusnog FIR filtera s pravokutnom graničnom frekvencijom prozora za vrijednosti dužine filtera i na logaritamskoj skali
Komentar:
Tabela 1. Opseg propusnog opsega, prelaznog regiona i zaustavnog pojasa za dužinu filtera i
|
Dužina filtera |
Širina pojasa, Hz |
Prijelazno područje, Hz |
Zaustavni pojas, Hz |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Predavanje br. 10 "Digitalni filteri sa konačnim impulsnim odzivom" Prijenosna funkcija fizički ostvarivog digitalnog filtera konačnog impulsnog odziva (FIR filter) može se predstaviti kao (10.1). Prilikom zamjene u izrazu (10.1) dobijamo frekvencijski odziv FIR filtera u obliku Gdje Kašnjenje faze filter je definisan kao Grupno kašnjenje filter je definisan kao Posebnost FIR filtera je mogućnost implementacije konstantnih faznih i grupnih kašnjenja, tj. linearni fazni odziv (10.5), gdje a - konstantno. Ako je ovaj uslov ispunjen, signal koji prolazi kroz filter ne narušava njegov oblik. Da bismo izveli uslove koji osiguravaju linearni fazni odziv, zapisujemo frekvencijski odziv FIR filtera uzimajući u obzir (10.5) Izjednačavanjem realnog i imaginarnog dijela ove jednakosti dobijamo Podijelimo drugu jednačinu prvom, dobivamo Konačno možemo pisati Ova jednačina ima dva rješenja. Prvo kada a =0 odgovara jednačini Ova jednadžba ima jedinstveno rješenje koje odgovara proizvoljnom h (0) (sin (0)=0), i h (n)=0 za n >0. Ovo rješenje odgovara filteru čiji impulsni odziv ima jedan uzorak različit od nule u početnom trenutku. Takav filter nije od praktičnog interesa. Naći ćemo drugo rješenje za . U ovom slučaju, unakrsnim množenjem brojilaca i nazivnika u (10.8) dobijamo (10.11). Odavde imamo Pošto ova jednadžba ima oblik Fourierovog reda, njeno rješenje je, ako postoji, jedinstveno. Lako je vidjeti da rješenje ove jednačine mora zadovoljiti uslove (10.13), (10.14). Iz uvjeta (10.13) slijedi da za svaki redoslijed filtera N postoji samo jedno fazno kašnjenje a , pri čemu se može postići stroga linearnost faznog odziva. Iz uslova (10.14) slijedi da impulsni odziv filtera mora biti simetričan u odnosu na tačku za neparan N , i u odnosu na sredinu intervala (slika 10.1).
Frekvencijski odziv takvog filtera (za neparne N ) može se napisati u obliku (10.15). Izvođenje zamjene u drugom iznosu m = N -1- n , dobijamo (10.16). Pošto je h (n)= h (N -1- n ), tada se dva zbroja mogu kombinovati Zamena, dobijamo (10.18). Ako odredimo onda konačno možemo pisati Dakle, za filter sa linearnim faznim odzivom imamo Za slučaj čak N slično ćemo imati Zamjena u drugom zbroju, dobijamo Izvršavamo zamenu, dobijamo (10.24). Nakon što je odredio konačno ćemo imati Dakle, za FIR filter sa linearnim faznim odzivom i ujednačenim redosledom N se može napisati U nastavku ćemo, radi jednostavnosti, razmatrati samo filtere neparnog reda. Prilikom sintetiziranja funkcije prijenosa filtera, početni parametri su u pravilu zahtjevi za frekvencijski odziv. Postoji mnogo tehnika za sintetizaciju FIR filtera. Pogledajmo neke od njih. Budući da je frekvencijski odziv bilo kojeg digitalnog filtera periodična funkcija frekvencije, može se predstaviti kao Fourierov niz gdje su koeficijenti Fourierovog reda jednaki Može se vidjeti da su koeficijenti Fourierovog reda h(n ) poklapaju se sa koeficijentima impulsnog odziva filtera. Dakle, ako je poznat analitički opis potrebnog frekventnog odziva filtera, onda je moguće lako odrediti koeficijente impulsnog odziva, a iz njih i prijenosnu funkciju filtera. Međutim, u praksi to nije izvodljivo, budući da impulsni odziv takvog filtera ima beskonačnu dužinu. Osim toga, takav filter nije fizički ostvariv jer impulsni odziv počinje na -¥ , i bez konačnog kašnjenja ovaj filter će učiniti fizički realističnim. Jedna od mogućih metoda za dobijanje FIR filtera koji aproksimira dati frekvencijski odziv je skraćivanje beskonačnog Fourierovog reda i impulsnog odziva filtera, pod pretpostavkom da h (n)=0 na . Onda Fizička ostvarivost prijenosne funkcije H(z ) može se postići množenjem H(z) na . Gdje (10.32). S takvom modifikacijom prijenosne funkcije, amplituda filtera se ne mijenja, a grupno kašnjenje se povećava za konstantan iznos. Kao primjer, izračunajmo niskopropusni FIR filter sa frekvencijskim odzivom u obliku U skladu sa (10.29), koeficijenti impulsnog odziva filtera su opisani izrazom Sada iz (10.31) možemo dobiti izraz za prijenosnu funkciju Gdje (10.36). Amplitudne karakteristike izračunatog filtera za razne N prikazani su na slici 10.2.
Sl.10.2 Mreškanje u propusnom i zaustavnom pojasu nastaje zbog spore konvergencije Fourierovog niza, što je, zauzvrat, uzrokovano prisustvom diskontinuiteta u funkciji na graničnoj frekvenciji propusnog pojasa. Ove pulsacije su poznate kao Gibbs ripple. Sa slike 10.2 je jasno da sa povećanjem N frekvencija pulsiranja se povećava, a amplituda se smanjuje i na nižim i na višim frekvencijama. Međutim, amplituda posljednjeg talasa u propusnom opsegu i prvog talasa u zaustavnom pojasu ostaju praktički nepromijenjeni. U praksi su takvi efekti često nepoželjni, što zahtijeva pronalaženje načina za smanjenje Gibbsovih pulsacija. Skraćeni impulsni odziv h(n ) može se predstaviti kao proizvod traženog beskonačnog impulsnog odziva i nekih funkcije prozora w (n) dužine n (slika 10.3).
U razmatranom slučaju jednostavnog skraćivanja Fourierovog reda koristimo se pravougaoni prozor U ovom slučaju, frekvencijski odziv filtera može se predstaviti kao kompleksna konvolucija To znači da će to biti "zamućena" verzija tražene karakteristike. Problem se svodi na pronalaženje funkcija prozora koje omogućavaju smanjenje Gibbsovog talasanja uz istu selektivnost filtera. Da biste to učinili, prvo morate proučiti svojstva funkcije prozora na primjeru pravokutnog prozora. Spektar funkcije pravokutnog prozora može se zapisati kao Spektar funkcije pravokutnog prozora prikazan je na slici 10.4.
Fig.10.4 Budući da na , ispada da je širina glavnog režnja spektra jednaka . Prisustvo bočnih režnjeva u spektru funkcije prozora dovodi do povećanja Gibbsovog talasa u frekvencijskom odzivu filtera. Da bi se postiglo nisko talasanje u pojasu propusnosti i veliko slabljenje u zaustavnom pojasu, potrebno je da područje ograničeno bočnim režnjevima bude mali dio površine ograničene glavnim režnjem. Zauzvrat, širina glavnog režnja određuje širinu prijelazne zone rezultirajućeg filtera. Za visoku selektivnost filtera, širina glavnog režnja treba biti što manja. Kao što se može vidjeti iz gore navedenog, širina glavnog režnja opada sa povećanjem reda filtera. Dakle, svojstva odgovarajućih prozorskih funkcija mogu se formulirati na sljedeći način: - funkcija prozora mora biti vremenski ograničena; - spektar funkcije prozora treba najbolje aproksimirati funkciju ograničenu frekvencijom, tj. imaju minimum energije izvan glavnog režnja; - Širina glavnog režnja spektra funkcije prozora treba biti što je moguće manja. Najčešće korištene funkcije prozora su: 1. Pravokutni prozor. Raspravljano gore. 2. Hamingov prozor. Gdje . Ovaj prozor se zove Hannov prozor ( hanning). 3. Blackman prozor. 4. Bartletov prozor. Indikatori filtara izgrađenih korištenjem specificiranih funkcija prozora sumirani su u Tablici 10.1.
Faktor valovitosti je definiran kao omjer maksimalne amplitude bočnog režnja prema amplitudi glavnog režnja u spektru funkcije prozora. Da biste odabrali traženi redoslijed filtera i najprikladniju funkciju prozora prilikom izračunavanja stvarnih filtera, možete koristiti podatke iz Tablice 10.2.
Kao što se može vidjeti iz Tabele 10.1, postoji određena veza između koeficijenta valovitosti i širine glavnog režnja u spektru funkcije prozora. Što je manji koeficijent pulsiranja, veća je širina glavnog režnja, a time i prijelazna zona u frekvencijskom odzivu filtera. Da bi se osiguralo nisko valovanje u propusnom pojasu, potrebno je odabrati prozor s odgovarajućim koeficijentom valovitosti i osigurati potrebnu širinu prijelazne zone sa povećanim redoslijedom filtera N. Ovaj problem se može riješiti korištenjem prozora koji je predložio Kaiser. Kaiserova prozorska funkcija ima oblik
gdje je a nezavisni parametar,
Privlačno svojstvo Kaiserovog prozora je mogućnost glatke promjene koeficijenta pulsiranja od malih do velikih vrijednosti, uz promjenu samo jednog parametra a. U ovom slučaju, kao i za druge funkcije prozora, širina glavnog režnja može se podesiti redoslijedom filtera N. Glavni parametri postavljeni prilikom razvoja pravog filtera su: Širina pojasa - w p ; Traka s preprekama - w a ; Maksimalno dozvoljeno talasanje u propusnom opsegu je A p ; Minimalno slabljenje zaustavnog pojasa – A a ; -frekvencija uzorkovanja - ws. Ovi parametri su ilustrovani na slici 10.5. U ovom slučaju, maksimalno talasanje u pojasu propusnosti određuje se kao
a minimalno slabljenje u zaustavnom pojasu je kao Relativno jednostavan postupak za izračunavanje filtera s Kaiser prozorom uključuje sljedeće korake: 1. Određuje se impulsni odziv filtera h (n), pod uvjetom da je frekvencijski odziv idealan
gdje je (10.49). 2. Parametar d je odabran kao
Gdje 3. Prava vrijednost A a i A p izračunava se pomoću formula (10.46), (10.47). 4.Parametar a je odabran kao
5.Parametar D je odabran kao
6. Odaberite najmanju neparnu vrijednost reda filtera iz uvjeta
sledi to Budući da su uzorci impulsnog odziva filtera koeficijenti njegove prijenosne funkcije, uvjet (10.59) znači da kodovi svih koeficijenata filtera sadrže samo razlomački dio i bit predznaka, a ne sadrže cijeli broj. Broj cifara razlomnog dijela koeficijenata filtera određuje se iz uvjeta zadovoljavanja funkcije prijenosa filtra s kvantiziranim koeficijentima, specificiranih zahtjeva za približavanje referentnoj prijenosnoj funkciji sa tačnim vrijednostima koeficijenata. Apsolutne vrijednosti uzoraka ulaznog signala filtera se obično normaliziraju tako da Ako se analiza provodi za FIR filter s linearnim faznim odzivom, tada algoritam za izračunavanje njegovog izlaznog signala može biti sljedeći gdje su koeficijenti filtera zaokruženi na s k. Ovaj algoritam odgovara blok dijagramu filtera prikazanom na slici 10.5.
Postoje dva načina za implementaciju ovog algoritma. U prvom slučaju, sve operacije množenja se izvode tačno i nema zaokruživanja proizvoda. U ovom slučaju, dubina bita proizvoda jednaka je s u +s k, gdje je s in dubina bita ulaznog signala, a s k je dubina bita koeficijenata filtera. U ovom slučaju, blok dijagram filtera prikazan na slici 10.5 tačno odgovara stvarnom filteru. Kod drugog načina implementacije algoritma (10.61) svaki rezultat operacije množenja se zaokružuje, tj. proizvodi su izračunati sa određenom greškom. U ovom slučaju potrebno je promijeniti algoritam (10.61) kako bi se uzela u obzir greška unesena zaokruživanjem proizvoda Ako se vrijednosti uzorka izlaznog signala filtera izračunaju pomoću prve metode (sa tačnim vrijednostima proizvoda), tada se disperzija izlaznog šuma određuje kao
one. ovisi o varijansi šuma zaokruživanja ulaznog signala i vrijednosti koeficijenata filtera. Odavde možete pronaći potreban broj bitova ulaznog signala kao
Koristeći poznate vrijednosti s in i s k, može se odrediti broj bitova potrebnih za frakcijski dio koda izlaznog signala kao Ako se vrijednosti uzoraka izlaznog signala izračunaju pomoću druge metode, kada se svaki proizvod zaokruži na s d znamenki, tada se disperzija šuma zaokruživanja koju stvara svaki od množitelja može izraziti u smislu cifrenog kapaciteta proizvod kao DR ulaz i odnos signal-šum na izlazu filtera SNR out. Dinamički opseg ulaznog signala u decibelima je definisan kao
gdje su A max i A min maksimalne i minimalne amplitude ulaznog signala filtera. Odnos signal-šum na izlazu filtera, izražen u decibelima, definisan je kao
određuje srednju kvadratnu vrijednost snage izlaznog sinusoidnog signala filtera amplitude A min, i (10.77) određuje snagu buke na izlazu filtera. Iz (10.75) i (10.76) sa A max =1 dobijamo izraz za disperziju izlaznog šuma filtera Ova vrijednost disperzije izlaznog šuma filtera može se koristiti za izračunavanje dubine bita ulaznih i izlaznih signala filtera.  Svijet besplatnih programa i korisnih savjeta 2024 whatsappss.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(10.2),
- amplitudno-frekvencijski odziv (AFC) filter,
- fazno-frekventni odziv (PFC) filter.
(10.3).
(10.4).
(10.6).
(10.7).
(10.8).
(10.9).
(10.10).
(10.12).
(10.17).
(10.19),
(10.20).
(10.21).
(10.22).
(10.23).
(10.25),
(10.26).
(10.27).
(10.28),
(10.29).
(10.30).
(10.31),
(10.33).
(10.34).
(10.35),
(10.37).
(10.38).
(10.39).
(10.40).
(10.41),
(10.42).
(10.43).
(10.44),
, I 0 – Beselova funkcija prve vrste nultog reda, definisana izrazom
(10.45).
(10.46),
(10.50),
(10.51).
(10.52).
(10.53).
(10.54),
(10.57)
(10.66),
(10.67).
(10.74),
(10.75),
(10.78).